改进的LeNet-5模型在花卉识别中的应用

吴丽娜，王林山

(中国海洋大学 数学科学学院，山东 青岛 266100)

0 引 言

卷积神经网络模型是一种具有高学习效率，非线性映射能力以及较强的鲁棒性和容错性的深度学习模型[1,2]，因此该网络被广泛关注，它的理论和应用研究是人工神经网络领域的热点之一。

卷积神经网络有多种形式，如，在海量图像分类领域取得突破性成果的Alex Net模型[3]；适用于目标检测的R-CNN(regions with CNN)[4]模型；能够实现端到端的图像语义分割的全卷积网络(fully convolution networks，FCN)模型[5]，应用于图像的摘要生成和图像内容问答的RNN[6,7]模型。尤其是应用于手写字符识别、图像分类的LeNet-5卷积神经网络模型，是由LeCun提出的一种典型的用来识别手写数字的卷积神经网络模型[8]，在计算机视觉领域有广泛的应用和改进：如，李勇等[9]用了跨连接的思想, 提出一种新的LeNet-5卷积神经网络模型，将其用于面部表情识别，并在JAFFE表情公开库和CK+数据库取得了较好的识别效果；马苗等[10]去掉基本LeNet-5中的第3卷积层,并用SVM分类器代替输出层中的Softmax分类器，在国际公开的SVHN数据集的实验结果表明，改进的LeNet-5对街景门牌号码的识别效果较好，并达到了较高的识别率；特别是刘德建等[11]成功地应用经典LeNet-5卷积神经网络成功地研究花卉识别问题，存在着进一步提高花卉图像识别率的问题。本文在文献[11]的基础上，试图对LeNet-5卷积神经网络进行改进，并对Oxford-17(17 category flower datasets)花卉数据集进行测试，实验结果表明，改进的LeNet-5卷积神经网络对花卉图像的识别率达到96.5%，比未改进的LeNet-5卷积网络提高了6.5%。

1 LeNet-5卷积网络模型

LeNet-5卷积网络模型(如图1所示)不包括输入层，总共有7层，包括：C1卷积层，S2池化层，C3卷积层，S4池化层，C5卷积层，F6全连接层，Output输出层。输入的图像是32×32像素的图像。C1卷积层有6张特征图，其运算方式是每个特征图中的每个单位都与输入图中的 5×5 像素的区域相连，且每个特征图都通过6个5×5像素大小的卷积核进行卷积操作，从而得到6个28×28像素大小的特征图。S2池化层包括6张特征图，与C1卷积层中的特征图数目相等，该层每张特征图的大小为14×14像素,其运算方式是每个特征图的单元都与C1卷积层中的每个特征图的2×2像素的区域相连。C3卷积层有16张特征图，其运算方式是每个特征图都通过5×5像素的卷积核与S2池化层中的某几个或全部特征图进行卷积操作得到，见表1。S4池化层共有16个5×5像素大小的特征图，其运算方式是该层特征图的每个单元都与C3层每个特征图的 2×2 像素区域相连。C5卷积层共有120个特征图，每个特征图单元都与S4层所有特征图5×5像素的区域相连，该层的特征图都通过5×5像素的卷积核与S4层的所有特征图进行卷积操作得到，所以该层特征图的大小为1×1像素。F6全连接层共有84个单元, 并且F6层与C5层是全连接的。Output输出层采用的是欧式径向基函数(RBF)。

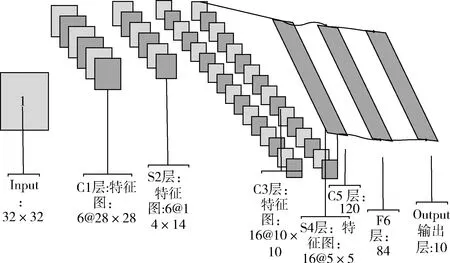
图1 LeNet-5网络结构

表1 S2与C3的连接方式

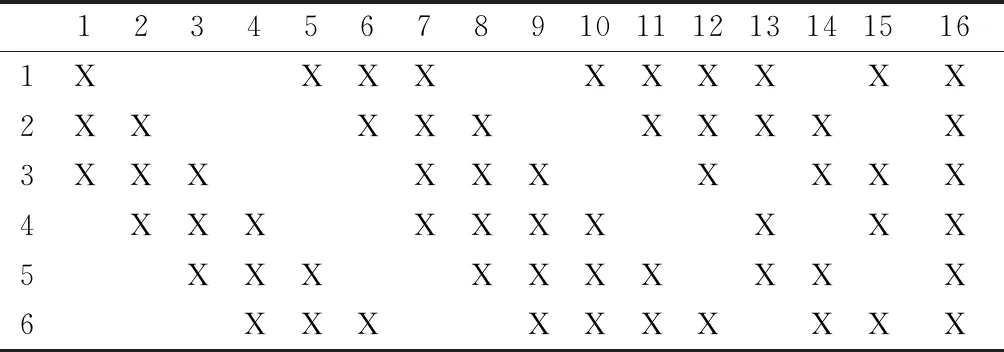
123456789101112131415161XXXXXXXXXX2XXXXXXXXXX3XXXXXXXXXX4XXXXXXXXXX5XXXXXXXXXX6XXXXXXXXXX

2 LeNet-5卷积网络模型的改进

LeNet-5卷积神经网络模型最初是通过卷积核自动提取特征，将原始数据通过一系列的非线性变换转化为高维特征，从而对高维特征进行分类。但是这种分类方法没有考虑到低维的细节特征，且随着深度的增加，易出现梯度消失或爆炸问题[12]。为了解决此类问题，使得低维细节特征均匀地传递给下一层，并将高维的突出特征全部传递给输出层，本文主要从池化操作方式以及S4层与C5层的连接方式入手，并针对花卉以及花瓣与手写数字字符存在形态上的差异，在不考虑同一类别的花卉有很大的差异性以及图像背景复杂的前提下[13]，对原LeNet-5卷积神经网络模型进行如下改进和与文献[11]不同的参数设置，以此为基础给出新的训练算法：

(1)关于池化操作的改进：S2层的池化操作设置为均值池化(Avg-pooling)，且S4层的池化操作设置为最大池化(Max-pooling)；

(2)关于连接方式的改进：将C5层设置为全连接层，即将S4层与C5层之间的5×5卷积核去掉，使两层的特征图以全连接的方式相连。

(1)

其中，f为激活函数，bj为偏置向量(bias)，n表示S4层神经元的个数。k表示C5层神经元的个数。图2为LeNet-5网络拓扑图。

图2 LeNet-5网络拓扑

2.1 参数设置

(1)在F6层之后、输出层之前使用Dropout正则化方法。

(2)将激活函数设置为ReLU激活函数

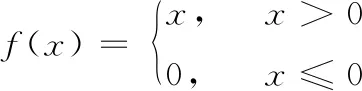
(2)

(3)算法：使用随机梯度下降算法SGD(stochastic gradient descent)[14]更新权值参数。SGD算法原理公式

(3)

(4)

(5)

其中，h(α) 表示拟合函数，J(α) 表示损失函数，α=(α1,α2,…,αn) 表示网络参数权值，yi表示第i个样本的样本值，m表示的是整个迭代进行的总次数,j表示网络中参数的总数目，α′j表示更新后的网络参数。

(4)分类器的确定：选用Softmax分类器。对于Output层,输入x， 则有

(6)

其中，ω=(ω1,ω2,…,ωm)T表示权值，P计算的是输入为j类别时的概率，设置输出类别为17。

2.2 参数设置理由

(1)S2层的均值池化操作，能够使得上一层中的低层次细节特征可以充分或均匀地出现在下一层的特征图中。S4层的最大值池化，可以保证C3层中更为突出的高层次特征传递给下一层(S4层)。

(2)将C5层设置为全连接层以后，图像的高维特征通过全连接的方式传递给下一层，取得的识别效果更好。

(3)Dropout方法是卷积神经网络中经典的正则化方法，实验中数据集并不是非常大，使用Dropout方法能有效减少过拟合现象。

(4)将激活函数替换为ReLU激活函数。使用传统的Sigmoid激活函数，需要预训练，否则会出现梯度消失无法收敛的问题。将激活函数替换为ReLU激活函数会使收敛速度更快[15]。

(5)随机梯度下降算法SGD每次只随机选择一个样本来更新模型参数，因此每次的学习是非常快速的。

(6)由于本次实验输出类别数为17，所以选择Softmax多分类器。

改进后的网络结构设置见表2，新网络结构如图3所示。学习率设置：本文分别考察了学习率为0.001和0.01对识别率的影响，实验结果表明，在相同条件下，学习率设置为0.001时，识别率更高。因此学习率设置为0.001。

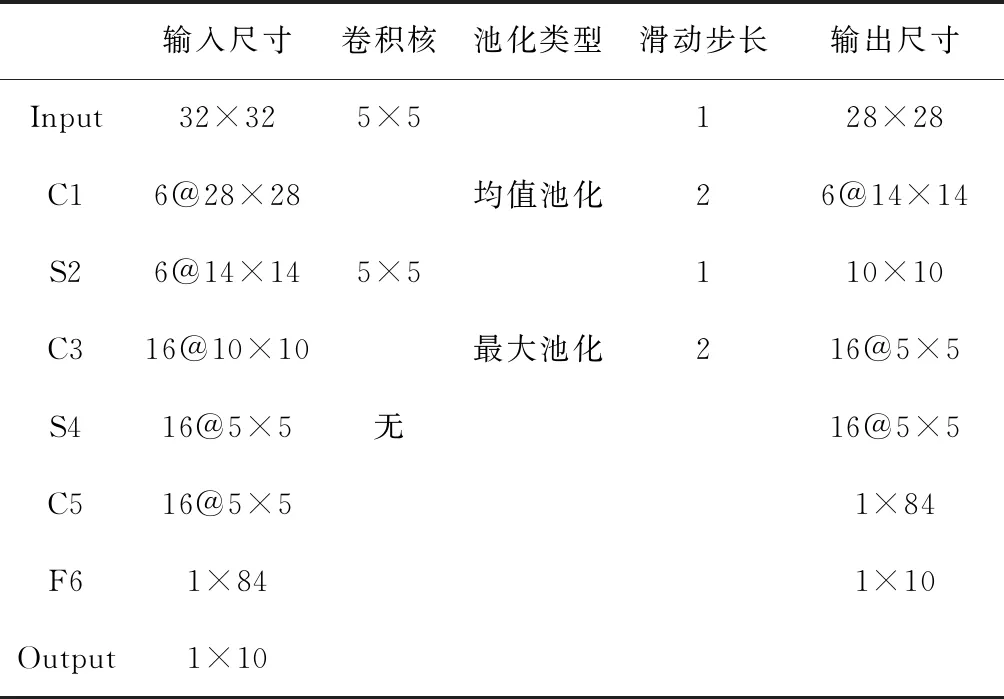
表2 新的LeNet-5网络结构

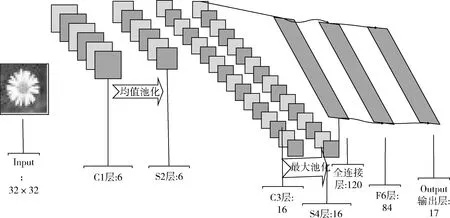
图3 新的LeNet-5网络结构

3 基于改进LeNet-5模型的花卉分类问题研究

3.1 数据集的选择

数据集是包含17个类别的牛津花卉(Oxford-17 flo-wer)数据集，该数据集是由牛津大学Visual Geometry Group创建的。每个类有80幅图像，总共有1360张图像，本文选取其中1000张图像作为训练样本，200张作为测试样本集。图4是实验中部分花卉图像。

图4 部分彩色花卉图像

3.2 图像预先处理

图像预处理一般是指对输入的数字图像进行颜色空间转换，高斯滤波等[16]。颜色是花卉图像最显著的特征之一，具有形状和方向无关性，适合作为花卉种类识别的依据[17]。但是颜色会对花卉种类的识别造成一定的干扰，每类花的颜色，拍照时图像的亮度都对花卉种类的识别产生较大的影响，彩色图像存储量大，处理不方便，需要将彩色图像转化为包含同样信息量且处理过程更加简单快速的灰度图像[18,19]。

使用matlabR2016将收集到的图像进行预处理：先将所有图像统一转化为单通道的灰度图像, 灰度级设置为8，并对数据集进行批量人工标号。其次，将图像的分辨率统一转化为28×28大小的分辨率，最后使用VS2013和Opencv3.1将图像转化为相应的二进制格式文件。图5～图7 表示部分灰度图像、向日葵放大灰度图像和识别错误图像。

图5 一些灰度图像

图6 向日葵的放大灰度

图7 识别错误的图片

3.3 实验环境的介绍

硬件环境：

本次实验是在牛津花卉数据库上进行的实验，考虑到数据量不是很高，以及网络深度并没有很大，所以实验数据放在单CPU上进行处理，实验硬件环境见表3。

软件安装及配置：

实验中所用的深度学习框架是tensorFlow[20]，编程语言是Python3.5.4，辅助软件工具是matlabR2016，Opencv3.1和VS2013。

tensorFlow是一个非常强大的用来做大规模数值计算

表3 硬件环境

的库。其所擅长的任务就是实现以及训练深度神经网络。它已经在大量移动设备上或者大规模分布式集群中使用，已经经过了实践检验。其分布式实现是基于图计算，它将图分割成多个子图，每个计算实体作为图中的一个计算节点[21]。本文最终得到的图表则是应用了tensorboard这一可视化工具。

3.4 实验步骤

(1)初始化卷积核，偏置向量(bias)。

(2)设置训练参数，将学习率设置为0.001，批训练样本数量batch设置为100，迭代次数epochs=2000，每次训练batch个样本数量。每100次迭代输出一次结果，最后输出总识别率。

(3)输入样本，正向传播和误差反向传播，用SGD更新权值参数。

(4)启动tensorboard，借助谷歌浏览器打开相关网址，将训练过程可视化。

为了验证改进后的新模型的可行性，从总样本中不同种类的花瓣集选取了共100张图片进行检验(即设置validation_size=100)。整个实验，没有使用GPU及CUDA加速，在单CPU上的训练时间是3.5小时左右。

3.5 实验结果与评价

改进LeNet-5网络模型部分实验输出结果展示：

test Accuracy at step 0:0.16

test Accuracy at step 500:0.64

test Accuracy at step 1000:0.88

test Accuracy at step 1500:0.94

test accuracy 0.965

实验中，在原LeNet-5网络模型上进行训练，训练到第1000步的时候，识别正确率达到0.88，在迭代到1500步的时候，识别结果达到0.94，总体识别率为0.965，图8为交叉熵(cross_entropy)变化曲线图，识别正确率(accuracy_1)变化曲线如图9所示。

图8 改进的LeNet-5神经网络模型交叉熵变化曲线

图9 改进的LeNet-5神经网络模型 识别正确率变化曲线

对于相同的样本数据集，每个模型每100步记录一次结果,总共记录10次，对比结果如图10所示,图10中，横轴step为迭代步数，纵轴Accuracy为识别正确率。由此结果对比可以得出，改进的LeNet-5卷积神经网络比BP神经网络和原LeNet-5卷积神经网络具有更高的识别精度。

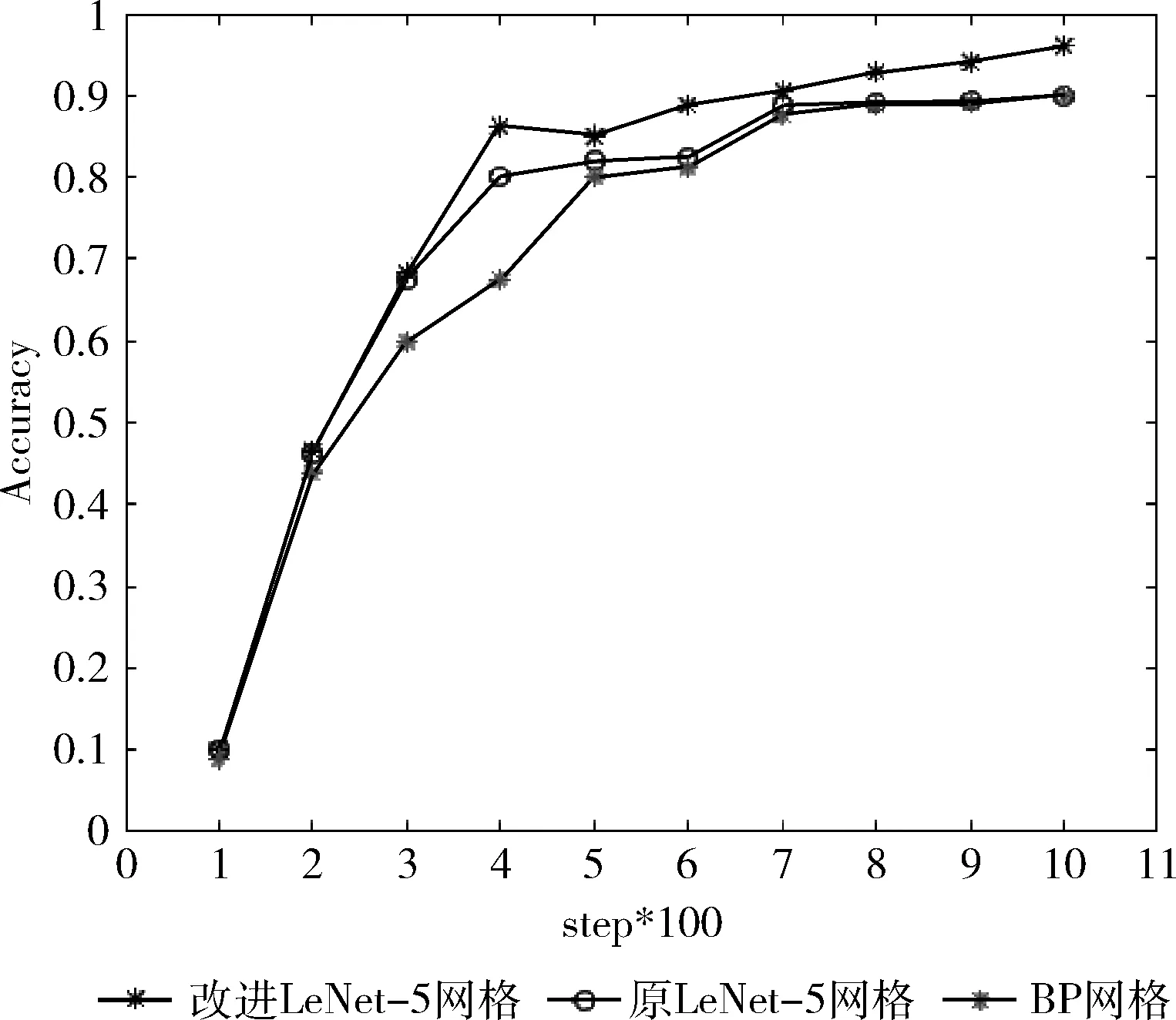
图10 3种网络模型对比结果

表4为在新的LeNet-5网络中，设置不同学习率得到不同的识别率，由此结果可以看出，控制其它参数条件不变，调节学习率这项参数，发现，当学习率设置为0.001时，识别率更高。表5为在新的LeNet-5网络中其它参数设置不变的情况下，不同激活函数对识别率的影响。表6为在新的LeNet-5网络中，使用Dropout正则化方法对识别率的影响，显然，在其它参数设置不变的情况下，有无Dropout对识别正确率的影响比较大。表7为实验数据放在3种不同的网络模型中得到的识别精度，显然，改进的LeNet-5网络比其它两种网络模型对实验数据有更好的识别效果。

表4 不同学习率对应识别率结果

表5 不同激活函数对应识别率结果

表6 有无Dropout对识别率的影响

表7 3种网络模型结果对比

4 结束语

本文在经典的LeNet-5卷积神经网络模型的基础上，将S2层的池化操作设置为均值池化，且S4层的池化操作设置为最大池化，S4层与C5层的连接方式设置为全连接，得到一类新的LeNet-5卷积神经网络模型，并将其应用于花卉种类识别。实验结果表明，改进的LeNet-5卷积神经网络模型可以达到提高花卉分类识别率的目的。但同时存在如下需要进一步改进的问题：

(1)本文对图像做了灰度化处理，没有考虑颜色对识别精度的影响，颜色对于测试结果有何影响还尚未给出讨论；

(2)是否还有更好的改进方法或者模型，适合研究花卉种类识别的工作，使得识别效果更好，在下一步的工作中将继续研究。