基于差异点集的频繁项集挖掘算法

尹 远，朱璐伟，文 凯

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆邮电大学 通信新技术应用研究中心，重庆 400065；3.重庆信科设计有限公司， 重庆 401121；4.中国电信股份有限公司 重庆分公司，重庆 401121)

0 引 言

挖掘关联规则之前最重要且繁琐的一步是频繁项集的挖掘，频繁项集挖掘算法可分为两种：①水平逐级搜索，例如崔馨月等[1]提出的Eclat改进算法，该算法采用位存储结构，减少了进行交集运算的项目所占内存；宋文慧等[2]提出基于矩阵的Apriori算法(M-Apriori)，该算法将数据库用上三角矩阵表示，可直接获取频繁1、2-项集，减少大量项候选项集的产生。②分而治之，例如何晴等[3]提出新的FP-Growth算法，该算法采用改进的哈希头表代替传统FP-Growth头表，通过合并最小支持度相同的节点压缩FP-tree，从而减少建树所占用的内存；李校林等[4]采用B-list结构表示项集，并结合子父等价修剪策略对搜索空间进行挖掘，时间性能大大提高。

针对传统阈值设置过大或过小带来不理想频繁项集数量的影响，Giang等[5]采用Top-rank-k挖掘模式挖掘可擦除项集，并提出一种新的dPID-list结构，减少了节点信息冗余度。Deng等[6]采用Node-list结构表示项集，并可通过项集交集运算快速获取项集支持度，提高了算法时间效率。

本文提出的基于差异点集[7]的DNTK算法，采用差异点集结构中特有的差集运算方法，避免了项集间复杂的连接过程；结合一种线性时间复杂度连接方法和早期修剪策略[8]，提出一种更为高效的1-项集连接方法来避免项集节点间无效连接；采用包含索引策略[9]来减少项集连接次数。

1 相关知识

1.1 频繁项集

定义1k-项集：对于集合P属于I，称集合P为一个项集，包含k个项目的项集称为k-项集。

定义2 频繁k-项集：对于给定的事务数据库DB，min-sup为用户给定的最小支持度，如果sup(X)≥min-sup×|DB|, 则称X为频繁项集。如果X为k-项集，则称为频繁k-项集。

定义3Top-rank-k频繁项集：给定一个数据集DB和阈值k，当且仅当RP≤k，项集P称为Top-rank-k频繁项集(RP为支持度大于等于项集P支持度的项集个数)。

1.2 差异点集(DiffNodeset)

近些年，许多数据结构被提出用来提高挖掘频繁项集的效率，例如Node-list，N-list[9]和Nodeset[10]。这三者都使用前缀编码树来表示项集信息，Nodeset结构与前两者不同之处在于Nodeset只需用pre-order或post-order来表示项集信息，因此其内存消耗较小，但随着数据集的增大，Nodeset的基数也会随之变大。针对该问题，本文将差异点集结构运用到Top-rank-k挖掘模式中，该结构所产生基数较Nodeset要小得多。

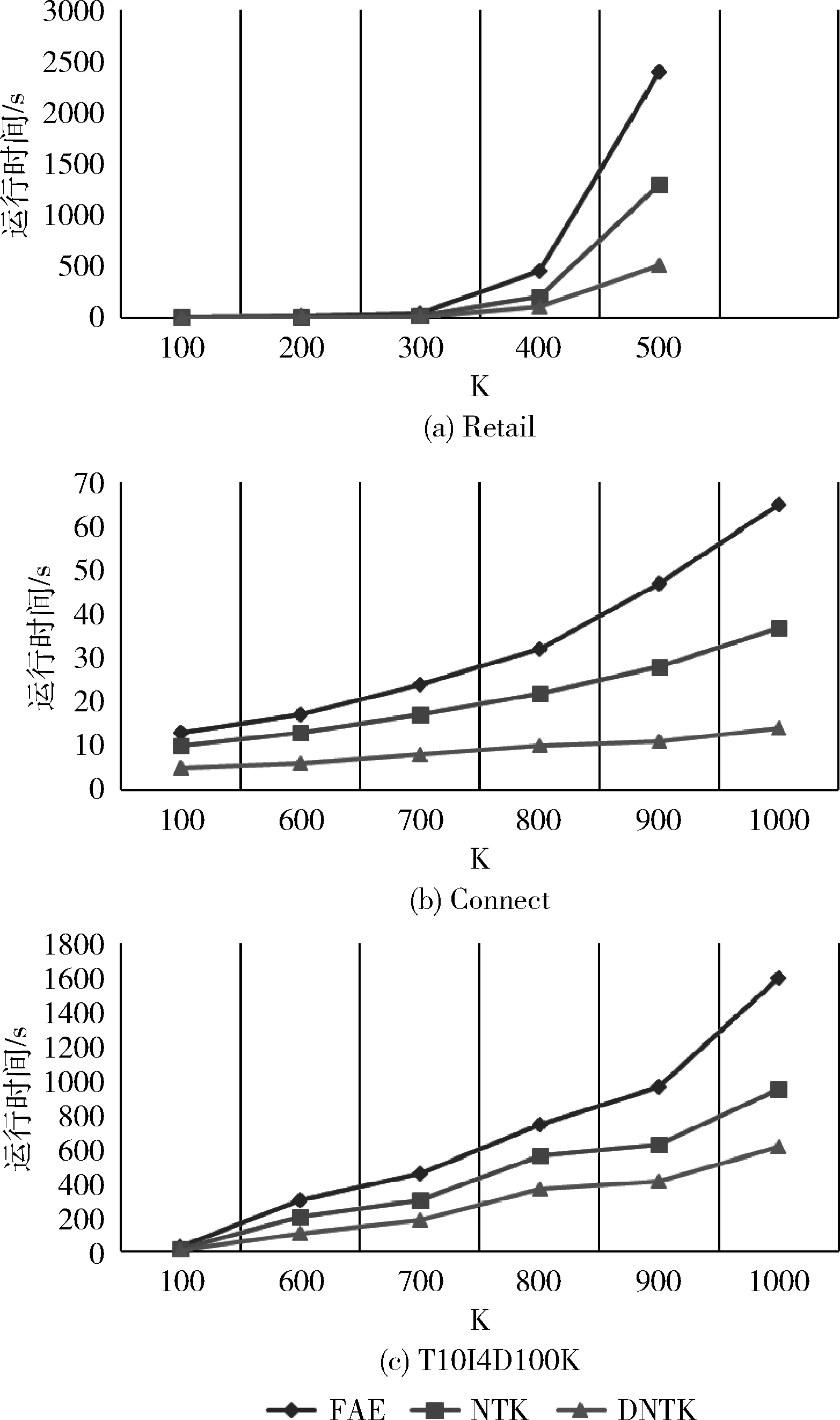
定义4 设L1为按支持度降序排列的频繁1-项集，对于任何两个项目i1和i2(i1,i2∈L1)， 我们表示i1

定义5 PP-code：对于PPC-tree中的每一个节点N，记PPN=[(N.pre-order，N.post-order，N.count)]， 因 (N.pre-order，N.count) 和 (N.post-order，N.count) 都可以表示N节点，因此这两种表示方法是等价的。

定义6 1-项集的Nodeset：对于给定的PPC-tree与节点P,所有名为P的节点的所有PP-code构成的集合称为其对应的Nodeset，记为NSP。其中所有PP-code按pre-order递增顺序排列。

定义7 2-项集的差异点集：设项目i1和i2(i1i2∈L1∩i1

(1)

性质1 设2-项集i1i2的DiffNodeset为DN12，项集i1i2的支持度表示为

sup(i1i2)=sup(i1)-∑(E∈DN12)E.count

(2)

详细证明过程请参考文献[7]。

性质2 设项集P=i1i2i3…ik(ij∈L1且i1

DNP=DN2/DN1

(3)

其中，/表示集合差。

详细证明过程请参考文献[7]。

性质3 设项集P=i1i2i3…ik且P1=i1i2…ik-2ik-1， 则项集P的支持度可按以下公式计算

sup(P)=sup(P1)-∑(E∈DNP)E.count

(4)

详细证明过程请参考文献[7]。

2 DNTK算法

2.1 改进的1-项集连接方法

早期修剪策略的算法步骤：

(1)分别计算1-项集ix和iy的Nodeset计数值，并表示为Cx和Cy；

(2)每一步，判定节点PPz若无父子关系，需确定PPz属于1-项集ix的Nodeset还是iy的Nodeset，若属于ix的Nodeset，更新Cx=Cx-PPz.count， 若属于iy的Nodeset，更新Cy=Cy-PPz.count；

(3)判定Cx或Cy，若小于阈值，则停止计算并返回空值。

文献[7]中项集连接方法Build_2-itemset_DN()可将两个项集的连接线性时间复杂度降为O(m+n),m和n分别代表两个项集的Nodeset大小。结合该项集连接方法和早期修剪策略，本文提出一种更为高效的项集连接算法Improved Build_2-itemset_DN()，该算法在项集连接过程中可及时判断其连接的可行性，避免了多次无效运算，伪代码如下：

Procedure Improved Build_2-itemset_DN(ixiy)

(1) DNxy=∅；

(2) k=0 and j=0；

(3) Cxbe the count of Nx(Nodesets of ix) and Cybe the count of Ny(Nodesets of iy)； //Cx:ix的支持度

(4) Let m=1;

(5) While k

(6) If Nx[k].post-order> Ny[j].post-order then

(7) Cy=Cy-m*Ny[j++].count；

(8) m=1；

(9) Else

(10) If Nx[k].post-orderNy[j].pre-order then

(11) m=0；

(12) k++;

(13) Else

(14) DNxy←DNxy∪{(Nx[k].post-order，Nx[k].count)}；

(15) Cx=Cx-Nx[k++].count；

(16) m=1；

(17) Endif

(18) Endif

(19) if(Cx

(20) k=Nx.size； //停止继续获取DNxy

(21) return NULL//DNxy返回为空， 且整个循环结束

(22) end if

(23) Endwhile

//若返回不为空值， 把ix的剩余节点都归为DN(ixiy)

(24) If k

(25) While k

(26) DNxy←DNxy∪{(Nx[k].post-order， Nx[k].count)}；

(27) k++；

(28) Endwhile

(29) Endif

(30) Return DNxy

以文献[7]中PPC-tree为例，项集e和c的Nodeset分别为 {5,8} 和 {{2,2},{7,1},{10,2}}。 设阈值为4，首先比较节点2和节点5，由于节点2的前后序编码分别小于节点5的前后序编码，按伪代码第(13)行，则存在Nx[k].post-order

2.2 基于包含索引的频繁2-项集挖掘

定义8 频繁项集A的包含索引表示为subsume(A)，定义为

subsume(A)={B∈I|g(A)⊆g(B)}

(5)

其中，g(A)表示项集A的事务集合。

性质4 设项集P包含索引为subsume(P)={p1,p2…pm}， 项集P和集合 {p1,p2…pm} 的任何子集相结合的支持度等于项集P的支持度。详细证明过程参考文献[9]。

性质5 设项集A∈subsume(B),B∈subsume(C), 则项集A∈subsume(C)。 详细过程参考文献[9]。

本文将包含索引策略与改进后的1-项集连接方法Improved Build_2-itemset_DN()有效结合，即先将频繁1-项集X与其非包含索引子集的1-项集进行结合获取候选2-项集，然后利用Improved Build_2-itemset_DN()方法计算其差异点集，因此不需要产生项集X与其包含索引子集结合的候选2-项集，减少了项集连接次数，提高了算法时间效率。

2.3 基于包含索引的频繁k(k>2)-项集挖掘

根据性质2和性质3，可直接利用项集的差异点集做差集运算来获取k(>2)项集的支持度，避免了项集间利用子父关系进行连接，提高了时间效率。本文将包含索引策略和此差集方法进行有效结合，不需产生项集与其包含索引子集结合的候选项集，减少了项集连接次数，时间效率得到提高。

3 算法描述

DNTK算法具体流程如图1所示。

图1 DNTK算法流程

(1)支持度设为0，获取所有频繁1-项集，扫描数据库，建立PPC-tree；

(2)扫描PPC-tree，获取所有1-项集的Nodeset；

(3)获取所有1-项集的包含索引；

(4)设定值k，遍历每个1-项集并将其插入Top-rank-ktable中，该表中包含项集和支持度，支持度相同的项集在同一个条目中，条目的数量不超过k，并更新阈值为表中最小支持度；

(5)先遍历table中每个k-项集Y1，后遍历前k-1个项目与Y1前k-1个项目相同；最后一个项目与Y1最后一个项目不同且不为Y1的包含索引子集的每个k-项集Y2。若Y1和Y2满足阈值并且k=1，运用Improved Build_2-itemset_DN(ixiy)方法对项集Y1和Y2进行连接，并将项集Y1Y2的包含索引更新为Y1的包含索引，若两个项集连接后返回不为空值，将其插入表中，删除条目值大于k的条目并更新阈值为表中最小支持度。若Y1和Y2满足阈值并且k>1，将Y1和Y2进行差集运算，并将项集Y1Y2的包含索引更新为Y1的包含索引，若项集Y1Y2的支持度满足阈值，将其插入表中，删除条目值大于k的条目并更新阈值为表中最小支持度；

(6)重复步骤(5)，直到没有新的项集产生；

(7)将表中包含索引不为空集的项集与其包含索引每个子集进行结合产生新的项集，根据性质4，可直接将其插入到Top-rank-ktable中。

4 实验结果分析

本文将DNTK*与DNTK算法的运行时间比例在不同数据集中作对比(DNTK*为未采用包含索引策略的DNTK算法)，以测试采用了包含索引策略的DNTK算法因减少项集连接次数所带来的时间效益。并且本文将DNTK算法与FAE和NTK算法在运行时间和内存占用方面进行比较，以验证该算法的整体性能。用java语言在实验环境为Inter(R) Core(TM) i5 3317U @ 1.7GHz CPU，内存4 GB，64位操作系统设备上实现以上算法比较，各组实验中每种算法所挖掘的频繁项集数量和内容是相同的，确保了实验公平性。实验所用数据集为常用数据集Retail，Connect，T10I4D100K和T2K50K1D，见表1。实验通过改变top rank value(k)的大小来测试算法运行时间和内存占用的情况。DNTK*算法与DNTK算法的运行时间比例实验结果如图2所示，DNTK算法与FAE和NTK算法的运行时间和内存占用对比实验结果分别如图3和图4所示。

表1 数据集参数

图2 运行时间比例

图3 运行时间对比

图4 内存消耗对比

如图2所示，DNTK*算法与DNTK算法的运行时间比例在Connect和T2K50K1D数据集中随着k值增大而增大，在T2K50K1D数据集中运行时，当k接近800的时候，DNTK算法时间效率比DNTK*算法快约两倍。因此可得出以下结论：采用了包含索引策略的DNTK算法因减少了项集连接次数，其时间效率得到提高；尤其在k值增大的时候，项集连接减少的次数会随之增加。

如图3所示，3种算法的运行时间都随着k值增大而增大，在T10I4D100K数据集上运行时，DNTK算法的时间效率优于FAE和NTK算法尤其是在Table-rank-value(k)越来越大的时候。在数据集Retail上运行时，当k值接近500的时候，DNTK算法比FAE算法快约5倍，比NTK算法快约3倍。随着k值越来越小，DNTK算法的时间效率优势也越来越不明显。如图4所示，在内存消耗方面，这3种算法在不同数据集上的内存消耗都随着k值增大而增大，当k值较大时，由于差异点集的结构性优势，DNTK算法的内存消耗明显少于FAE和NTK算法。实验结果表明DNTK算法在不同类型数据集中都有着较高的时间效率与空间效率。

5 结束语

本文提出一种频繁模式挖掘算法-DNTK。该算法将一种树形结构差异点集运用在Top-rank-k挖掘模式中，利用差集运算快速获取k(>2)项集支持度；结合Build_2-itemset_DN()项集连接方法和早期修剪策略，本文提出一种更为高效的项集连接方法，该方法可及时发现项集连接的可行性，提高时间效率；在DNTK算法中引入包含索引策略，减少了项集连接次数，提高了时间效率。实验结果表明DNTK算法在不同的数据集中性能优于FAE和NTK算法。考虑数据集越来越大的情况和当前大数据环境，DNTK算法与Spark平台结合[11]将会是下一步的研究方向。