基于GAPSO算法的转台齿轮传动多目标优化研究*

付军豪，刘 康*，胥 云，张 明，熊奉奎

(1.四川轻化工大学 机械工程学院，四川 宜宾 644000；2.绵阳职业技术学院 机械工程学院，四川 绵阳 621000)

0 引 言

五轴机床是加工航空发动机叶片和复杂回转轴类零件的重要装备，转台是五轴机床的核心部分之一，其齿轮传动系统结构性能直接决定五轴机床的整体性能。根据五轴机床的设计要求，转台采用多级齿轮传动系统，在满足工作条件下要求转台的齿轮传动系统具有体积小、轻量化、传动平稳等特点。多级齿轮传动系统由于结构复杂，影响传动性能的因素众多，其结构优化设计是一个复杂问题[1-3]。

遗传算法(genetic algorithm，GA)具备可以直接对结构对象进行操作、不存在求导和函数连续性的限定、采用概率化的寻优方法等特点，能够实现较快收敛，寻优结果合理、鲁棒性好，所以遗传算法被广泛用于多目标优化设计问题。

张江红等[4]针对三齿并联内啮合齿轮泵，建立了以流量脉动最小以及齿轮机构体积最小的多目标函数的数学模型，采用遗传算法优化后的齿轮机构达到了减小流量脉动和减小齿轮机构总体积的目的；钱亚平等[5]使用遗传算法对推料机的齿轮传动系统分别进行了单目标以及多目标优化，结果表明多目标优化相比单目标优化后，齿轮系统的重合度增加，体积较小，优化效果明显；WANG Jian等[6]以摆线减速器为研究对象，以齿轮体积和齿轮传动效率为目标函数，采用遗传算法优化后得到了最小体积并最大化效率；曾晨等[7]对微耕机变速箱进行了体积和重合度的多目标函数建模，采用了SGA遗传算法和NSGA-Ⅱ遗传算法分别优化求解，结果表明NSGA-Ⅱ遗传算法优化结果更好。

本文以某航空发动机叶片五轴加工机床转台的传动系统为研究对象，考虑转台结构紧凑和传动平稳等特点，以齿轮传动系统体积和重合度为设计目标的优化模型，使用GAPSO算法[8-9]对优化模型进行多目标优化，以获得更轻量化的体积和更高的传动平稳性。

1 转台结构以及优化目标

转台的传动系统主要采用双齿轮消隙机构，如图1所示。

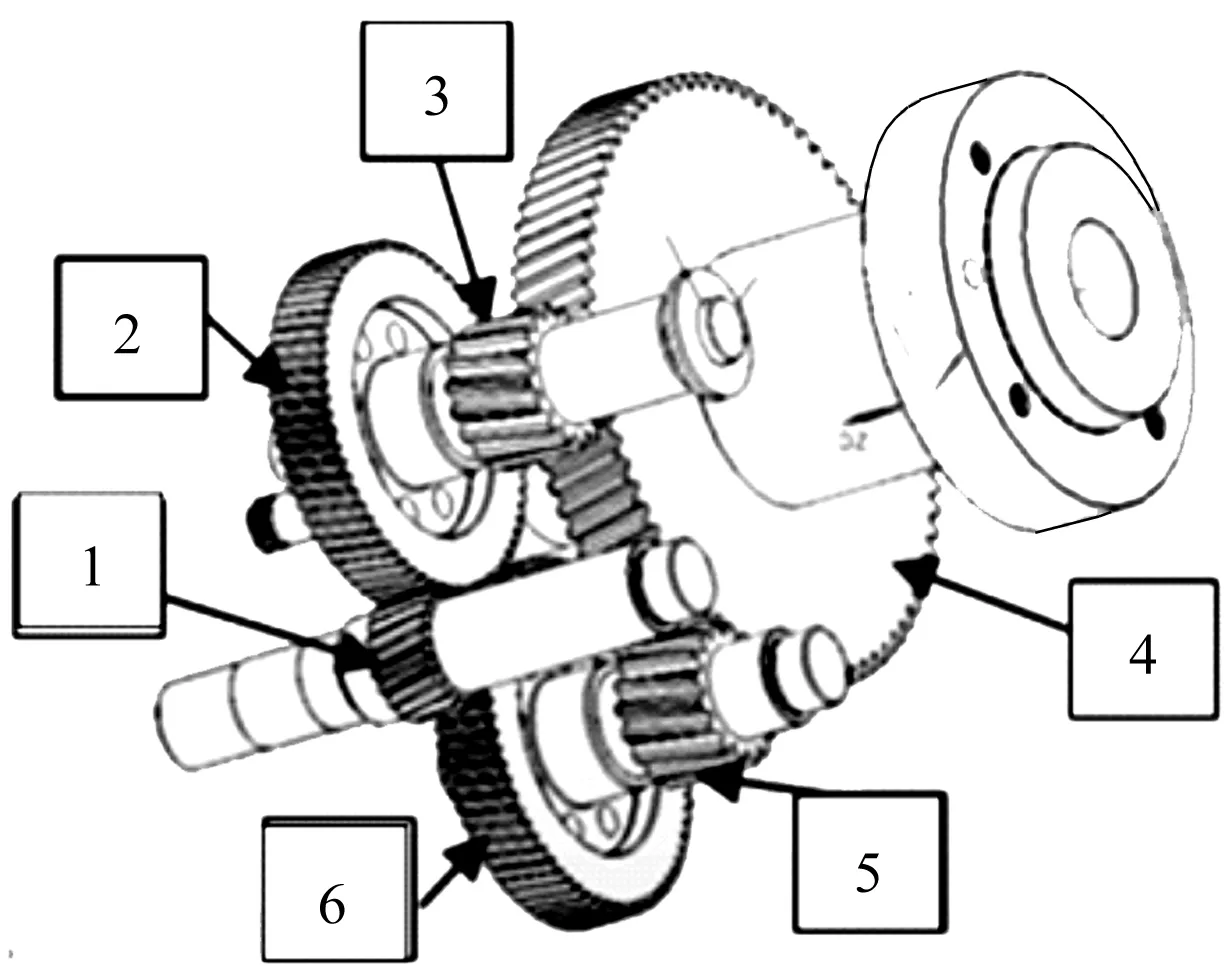
图1 转台齿轮传动系统装配图

转台采用西门子1FT6105-8AF7-4AGO型交流伺服电机驱动；电机额定转速3 000 r/min，输入功率9.7 kW；各级齿轮材料都使用20CrMnTi渗碳淬火，许用接触应力与许用弯曲应力分别为：[σH]=1 080 MPa，[σF]=835 MPa。

转台作为机床中的重要部分，对机床的整体性能起着非常重要的作用。在实际工作中，转台必须保持长时间平稳运行，减小齿轮传动系统的体积和增大齿轮传动的重合度可以有效提高齿轮传动的效率和稳定性。

本文主要考虑以转台传动系统所有齿轮的体积和重合度为目标函数。

2 转台优化设计数学模型

2.1 确定目标函数

在满足转台齿轮传动系统结构紧凑以及传动平稳的条件下，本文以总体积和总重合度作为目标函数，对转台齿轮传动系统进行优化。

2.2.1 体积目标函数

斜齿轮的体积可以近似看做为分度圆圆柱体体积，如图1所示，齿轮2与齿轮6相同，齿轮3与齿轮5相同，且转台齿轮传动系统结构对称布局，故以所有齿轮体积和作为体积目标函数，即：

(1)

式中：mn1,mn3—斜齿轮法向模数；z1,z3—斜齿轮1,3的齿数；i1—齿轮1与齿轮2的传动比；i2—齿轮3与齿轮4的传动比；β1,β3—齿轮1和齿轮3的螺旋角；φd1,φd3—齿轮1和齿轮3的齿宽系数。

2.1.2 重合度目标函数

转台齿轮传动系统的平稳性由重合度决定，重合度越大，齿轮传动越平稳，产生的冲击载荷越小。

本文以转台传动系统的齿轮的总重合度为目标函数，根据转台齿轮传动结构对称布局可知，重合度目标函数为：

(2)

2.2 设计变量

设计变量的变化可以直接改变目标函数，通过对体积目标函数和重合度目标函数的分析可知，选取齿轮1和3的模数、齿数、齿宽系数、螺旋角、齿轮1和2的传动比、齿轮3和4的传动比作为设计变量X：

X=[mn1,mn3,z1,z3,fd1,fd3,β1,β3,i1,i2]T=
[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10]T

(3)

目标函数f1,f2表达如下：

(4)

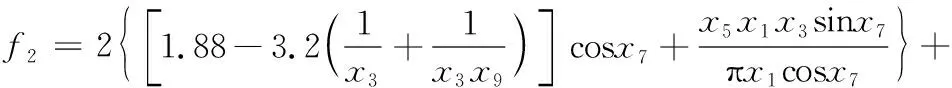
(5)

2.3 约束条件

2.3.1 齿面接触强度约束

根据机械设计手册第6版[10]的齿面接触强度校核的公式表可知，齿轮1和齿轮2的接触应力为：

(6)

齿轮3和齿轮4的接触应力为：

(7)

根据齿轮接触应力约束得：

σH1≤[σH]
σH2≤[σH]

(8)

式中相关参数查阅机械设计手册后带入设计变量得到：

(9)

(10)

2.3.2 轮齿弯曲强度约束

根据机械设计手册第6版的齿面接触强度校核的公式表可知，齿轮1和齿轮2的齿根应力为：

(11)

齿轮3和齿轮4的齿根应力为：

(12)

根据齿轮接触应力约束得：

σF1≤[σF]
σF2≤[σF]

(13)

式中相关参数查阅机械设计后，代入设计变量可得到：

(14)

(15)

2.3.3 边界条件约束

齿轮1和齿轮3的模数取值范围为：

0.5≤x1≤10，0.5≤x2≤10

(16)

齿轮1和齿轮3的齿数的取值范围为：

14≤x3≤30，17≤x4≤40

(17)

齿轮1和齿轮3的齿宽系数的取值范围为：

0.4≤x5≤1.2,0.4≤x6≤1.2

(18)

齿轮1和齿轮3的螺旋角的取值范围为：

8≤x7≤20，8≤x8≤20

(19)

齿轮1和齿轮3的传动比的取值范围为：

1≤x9≤10,1≤x10≤10

(20)

2.4 适应度函数

由于自身的局限性，标准遗传算法不能解决所有的优化问题，针对转台齿轮传动系统优化问题，本文采用罚函数寻优计算，将目标函数和约束条件相结合组成新的目标函数；将新的目标函数转换成适应度函数后通过加权系数把原来的多目标函数优化问题转化为单目标优化问题，加权系数值的大小体现每个目标函数的重要程度。本文对体积目标函数和重合度函数的加权系数分别取0.7,0.3；惩罚因子选取6。

体积函数与重合度函数的数量级相差较大，本文体积值数量级是106，单对齿轮重合度是1～2，所以转台齿轮传动系统最终求解目标函数为：

(21)

3 GAPSO算法与优化结果分析

3.1 GAPSO算法

根据以往相关文献对齿轮传动系统多目标优化方法的总结，一般都采用遗传算法(GA)对其进行寻优求解。本文在前人的工作基础上，利用粒子群优化算法(PSO)和遗传算法(GA)，结合彼此的优点，既有GA算法的强大全局搜索能力又有PSO算法的快速收敛能力，形成遗传粒子群算法(GAPSO)求解转台齿轮传动系统的多目标优化数学模型。

相比GA算法，GAPSO算法多了PSO算法对群体中优秀个体的筛选，经过PSO算法筛选后的优秀个体再经过交叉和变异得到剩下的个体，采用GAPSO算法得到个体得到相比GA算法得到的个体更加优秀。

GAPSO算法流程图如图2所示。

图2 GAPSO算法流程图

3.2 优化结果分析

根据求解目标函数f以及齿轮的接触强度约束、弯曲强度约束和边界条件约束，本文使用Matlab分别编写GA算法、PSO算法和GAPSO算法程序，得到转台齿轮传动系统多目标优化结果。其中，GAPSO算法的交叉概率为0.8，变异概率0.2，进化次数500，种群规模500。

3种算法所求设计变量如表1所示。

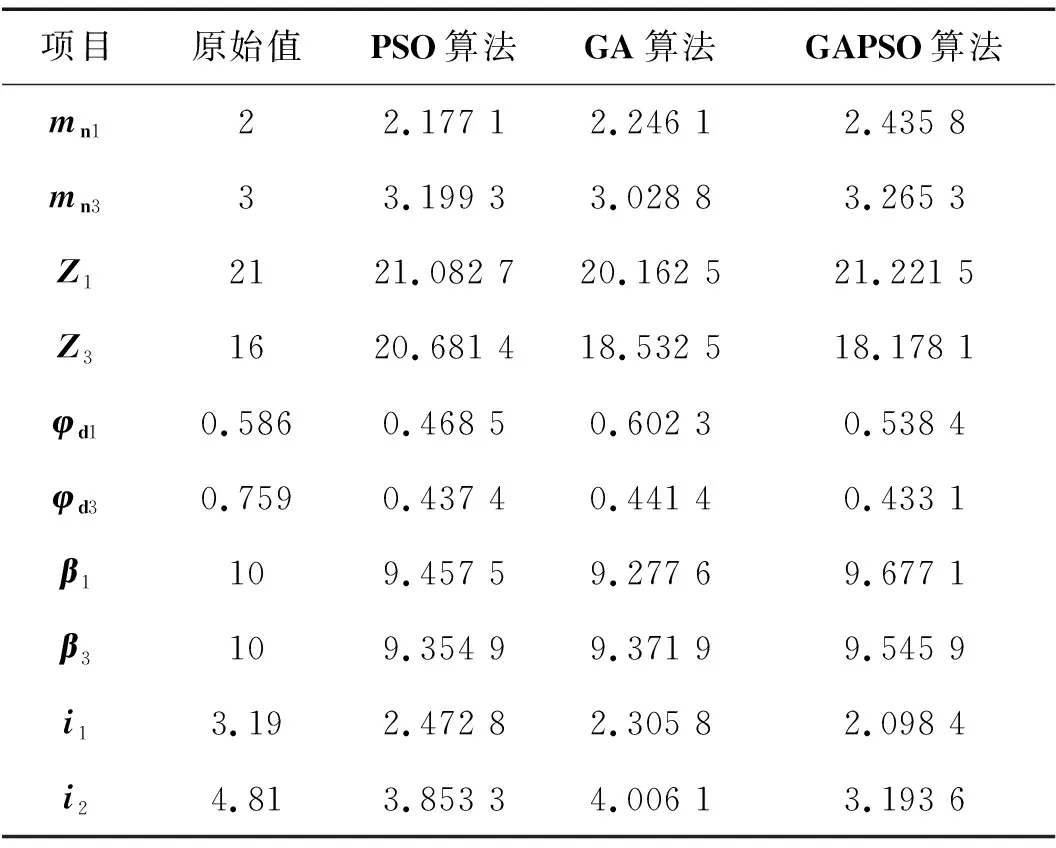
表1 各算法所求的设计变量

在3种不同算法下，转台传动系统齿轮的总重合度和总体积的变化的优化结果，如表2所示。

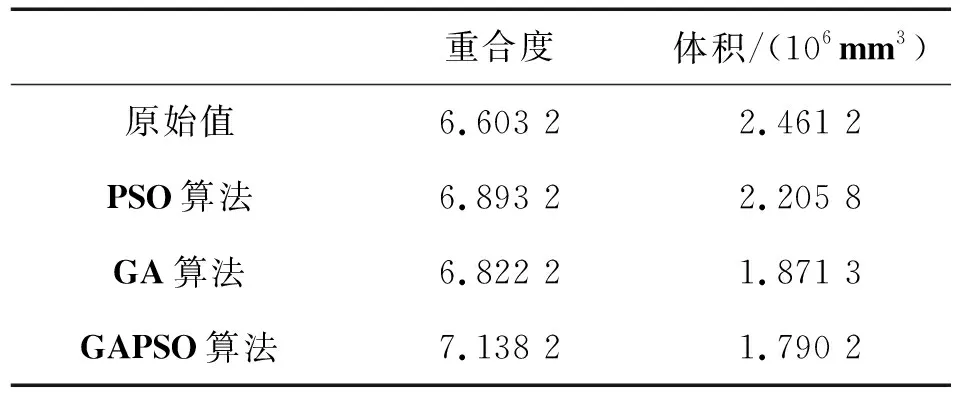
表2 各算法的优化结果

从表2可以看出：

采用PSO算法、GA算法、GAPSO算法优化后，转台齿轮传动系统的总体积分别减少10.38%、23.97%、27.26%；转台齿轮传动系统总重合度分别增加4.39%、3.32%、8.10%。优化结果综合表明GAPSO算法对转台齿轮优化效果最好。

4 结束语

本文主要对某航空发动机叶片五轴加工机床转台的齿轮传动系统进行了结构优化，从齿轮传动系统的轻量化和传动平稳性出发，建立了以体积和重合度为目标函数的数学模型，利用GAPSO算法寻优求解更快、精度更高的特点，对目标函数的数学模型进行了求解。

优化后的转台齿轮传动系统的体积减少27.26%，重合度增加8.10%；优化后的齿轮参数为：mn1=2，mn3=3，Z1=21，Z3=18，φd1=0.5，φd3=0.4，β1=10，β3=10，i1=2，i2=3。

优化后的转台齿轮传动系统有效地减小了转台的体积，在实现产品轻量化的同时，增加了转台齿轮传动系统的重合度，提高了转台传动系统的平稳性，也为五轴机床转台的结构优化设计提供了一种新思路。

参考文献(References):

[1] 焦映厚，陈照波，付 龙.大型立式齿轮箱行星齿轮传动系统的优化设计[J].机械传动，2012，36(6)：58-64.

[2] 张 席，李炳文，郝 亚，等.基于体积最优的调度绞车多级传动系统优化设计及性能分析[J].机械传动，2019，43(1)：75-84.

[3] 樊立梅.基于Matlab的斜齿轮传动多目标可靠性优化设计[J].机械设计与制造，2008(8)：15-16.

[4] 张江红，王思霞，蒋晓琴，等.基于遗传算法的多齿并联内啮合齿轮泵优化设计[J].现代制造工程，2018(4)：115-118.

[5] 钱亚平，张 瑜，顾寄南.基于遗传算法的推料机齿轮传动多目标优化设计[J].机电工程，2018，35(8)：805-810.

[6] WANG Jian, LUO Shan-ming, SU De-yu. Multi-objective optimal design of cycloid speed reducer based on genetic algorithm[J]. Mechanism and Machine Theory, 2016, 102(8): 135-148.

[7] 曾 晨，李 兵，王小勇，等.基于NSGA-Ⅱ算法的微耕机变速箱多目标优化设计[J].机械传动，2016，40(7)：87-91.

[8] 彭晓波，桂卫华，黄志武，等.GAPSO:一种高效的遗传粒子混合算法及其应用[J].系统仿真学报，2008(18)：5025-5027.

[9] 王 飞，王能河，张琼英，等.基于GA-PSO算法的ZigBee自组网最佳路由选择[J].计算机工程，2017，43(7)：75-79.

[10] 成大先.机械设计手册[M].6版. 北京：化学工业出版社，2017.