燃气埋地聚乙烯管道修补的应力研究

杨俊峰，邹骊飞，宫耀华，张徐岩

（沈阳燃气集团，辽宁沈阳 110005）

引言

城镇天然气中、低压燃气管道中70%使用聚乙烯管道。聚乙烯管以其耐腐蚀、重量轻、密封性好、管壁光滑、使用寿命长、过流能力大、施工速度快、运输安装方便以及适应场地沉降的大变形能力等优点，在国内外已经广泛使用。在未来城镇天然气管网建设中，聚乙烯管道将占更大比重。由于燃气管道多敷设于经济繁荣、人口稠密区域，加上地下管道复杂等不稳定因素，导致燃气管道事故发生概率大大增加。因此，针对燃气聚乙烯埋地管道进行力学分析，对保障人民群众的生命和财产安全具有重要意义[1]。

聚乙烯管道主要有韧性失效、脆性失效、焊接接头失效、表面失效和缺陷引起的失效［2］。国内外学者开展了对聚乙烯管道的大量研究：朱志彬等［3］计算了含球孔缺陷的聚乙烯管道热熔接头的力学性能；李明阳等［4］计算了不同覆土深度下埋地聚乙烯管道的力学性能；Folkman 等使用了Spangler 提出的爱荷华公式，预测了柔性埋地管道施加载荷下的挠度[5]。这些研究均未涉及有缺陷的埋地聚乙烯管道局部修复对应力分布的影响。本文将建立埋地聚乙烯管道修复模型，应用ANSYS 有限元分析软件，综合考虑土壤温度、管道载荷和缺陷形状的影响，为管道的寿命预测和风险评估提供依据。

1 ANSYS管道计算介绍

ANSYS 是集成力学、冷热、电磁于一体的通用有限元分析软件，具有完备的前处理功能、强大的求解器、方便的后处理功能等，被广泛应用于航空、航天、制造、土木工程领域及研究中。通过ANSYS建立所求问题的模型，划分单元，求解有限个数值，就可以近似模拟真实环境的未知量。借助于ANSYS 进行结构强度和刚度分析，可以清楚地了解整个结构的应力分布以及变形情况。一个典型的ANSYS分析过程可分为以下三个步骤：

(1)创建有限元模型，包括创建或读入几何模型、定义材料属性、划分单元(节点及单元)。

(2)施加载荷进行求解，包括施加载荷及边界条件并求解。

(3)查看结果，包括查看分析结果、检验分析是否正确。

2 埋地聚乙烯管道模型

2.1 问题描述

埋地聚乙烯管道的应力与形变是管道及其周围的土壤共同作用的结果。本研究，为了确定管道修复后产生应力的效果，分别采用了鞍形、半圆柱形、方形和圆形四种补丁进行修复，对不同形状的修补效果进行对比，为工程实践提供理论依据[6-7]。

2.2 模型假设

根据埋地聚乙烯燃气管道的特点，进行如下假设：①压力项只考虑管道内压和地面载荷的间接作用力；②管道缺陷形状规则，具有对称性；③管道周围土壤介质分布均匀；④管道与土壤接触完好，没有空隙。

2.3 边界条件与几何尺寸

以外径114.3 mm、壁厚10 mm 的PE80 埋地聚乙烯管道为计算模型，修补部分采用PE100 材质。聚乙烯管道埋在宽度为416 mm 的沟槽中，聚乙烯管顶距地面1150 mm，管道周围用是一层细砾石填满，地面被沥青覆盖。埋地管道回填共分为五个区域，区域的划分见图1，尺寸见表1。

每个区域土体的属性见表2。在管道内施加正压，管道正上方的土体均引入重力因子，在沥青层的上表面施加垂直向下的地面载荷，在管道的侧面施加对称的约束力。

参考华北地区的气温和埋地深度，假设夏季聚乙烯管的平均温度为30℃，冬季平均温度为10℃。根据压力用塑料管道和管件分类和设计标准ISO12162(2009)3.4 节中对塑料管道温度要求，以最不利30 ℃进行设计（使用寿命50 年[8]）PE80 的最小设计强度（MRS）为7.0 MPa，PE100 的MRS 值为8.7 MPa。

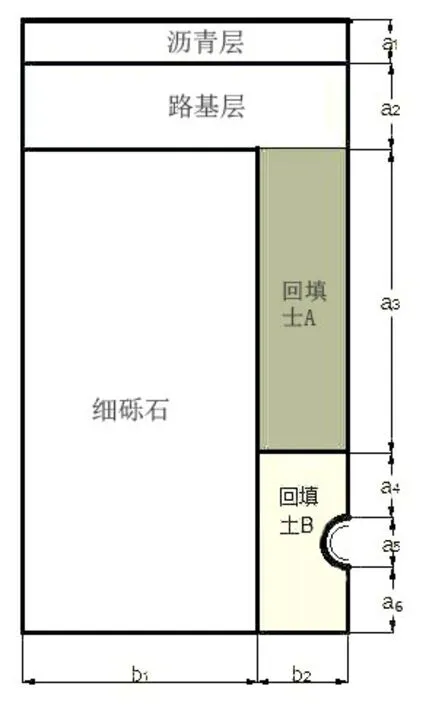
图1 埋地聚乙烯管道及土壤划分区域范围

表1 聚乙烯管道简化几何模型尺寸

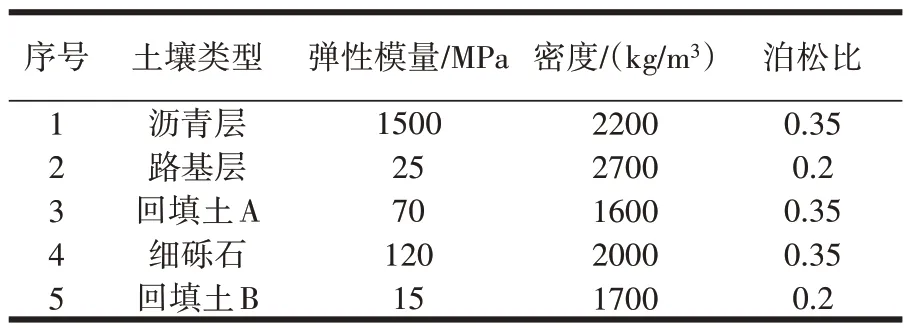
表2 管道周围土壤性质

针对目前我国城市燃气运行情况，埋地管道内部终压力假设为0.4 MPa，缺陷处孔径的直径尺寸从5mm 增加到20 mm，地面荷载变化范围0～50 kN/m2。

2.4 聚乙烯管道的有限元模型

模型网格由四部分组成，分别为管道无缺陷部分、管道缺陷部分、管道修补部分和土壤部分。缺陷按照形状分为圆孔型缺陷和裂缝形缺陷，假定管道缺陷部位位于管道正上部。埋地聚乙烯管道模型的网格划分如图2 所示，采用ANSYS15 中的solid65 单元与solid95 单元分别对管道和土壤进行分析。

四种修补形状如图3 所示。修补部分采用solid95 单元进行模拟，每个节点都有三个自由度（x、y和z 方向）。管道缺陷与修补部分、管道与土壤相互作用部分都综合被结合到模型中。修补材料选择PE100 材质的聚乙烯贴片，修补片的长度（图2 鞍形修补、半圆形修补和方形修补）或其直径（图2 圆形修补）假定为76 mm。图3 显示了管道修补的有限元模型及放大视图（在其缺陷区域上有贴片）。图4为椭圆形缺陷的管道网格图，a、b 为椭圆的短轴和长轴，a 为管道的，通过调整a/b 的数值可模拟不同裂缝形缺陷的应力影响。

图2 有限元中的修补形状

图3 埋地聚乙烯管道的网格划分与圆形缺陷放大视图

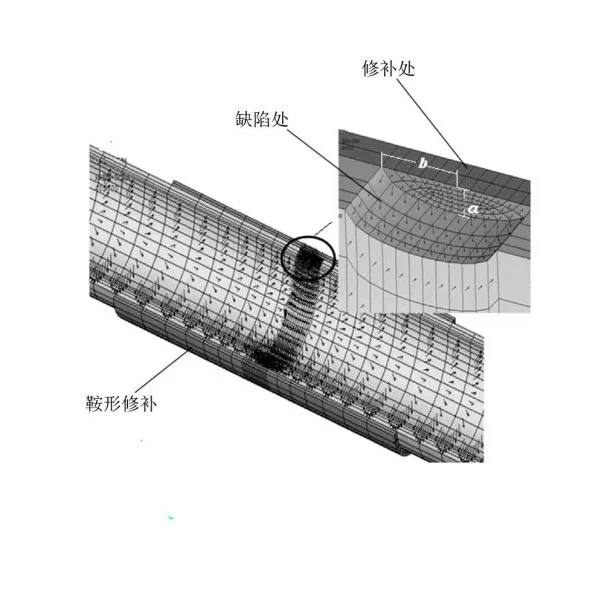
图4 带椭圆形缺陷的管道网格图

3 聚乙烯管道的荷载计算

埋地管道周围的土壤为管道上产生的静荷载，同时成为传递动荷载的介质，因此土壤的性质和荷载计算成为了埋地管道变形分析的基础。采用弹性梁理论建立埋地管线受力的静力分析模型，兼顾考虑管道埋深处环境温度变化对荷载的影响。

3.1 静荷载的力学计算

地面管道静载荷主要包括土壤重力、地面建筑物占压产生的压应力，假设土壤是均质的弹性体，静荷载仅考虑土壤重力产生的荷载，管道上方的静载荷产生的垂直压力作用在管道正的中央。采用Boussinesq 理论作为计算埋地管道静载荷的理论基础，其静载荷计算如公式（1）所示［9］。

式中：Ws－静荷载，kN/m2；

T－地面作用力，kN；

L－载荷作用面到管道顶部的垂直距离，m；

x－载荷作用点与管道顶部的长，m；

y－载荷作用点与管道顶部的宽，m；

z－载荷作用点与管道顶部的高，m。

3.2 动荷载的力学计算

管道上方车辆的运动是动载荷的主要来源。对于聚乙烯管道，埋深对管道动载荷的影响较大。埋地管道动载荷计算理论与静载荷计算理论基本一致，在Boussinesq 理论计算公式的基础上，通常乘以一个工程经验调整系数，其公式如（2）所示［9］。动荷载采用经过管道上方车辆动荷载为0～40 kN/m2时产生的荷载。

式中：Wd－动载荷，kN/m2；

S－动载荷集中调整系数；S取2.0。

总载荷为静载荷和动载荷之和，其公式如（3）所示。

3.3 聚乙烯管道挠度计算

计算聚乙烯管道挠度采用Sprangler的改良爱荷华公式[5]：

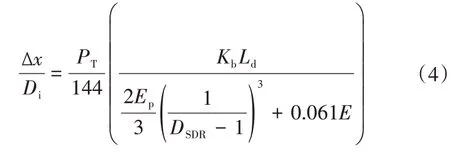
式中：Δx－管道的水平偏转量，mm；

PT－总荷载之和，kN；

Kb－变化系数（通常为0.1）；

Ld－偏转滞后因子；

Ep－管道弹性模量，MPa；

DSDR－管道壁厚，mm；

E－埋置土壤模量，MPa；

Di－管子的内径，mm。

3.4 热应力的计算

管道周围的土壤的温度在一天内会发生变化，每年也会发生季节性变化。埋地管道中产生的热应力计算是必需的[10]。计算公式如下：

式中：T（y，t）－土壤中的温度变化；

Tp－0～t时间内的平均温度；

y－土壤的的深度，mm；

A－当时的最高和最低温度之间的温差；

α－热扩散系数，mm2/s，根据前面假设的温度，该模型的埋地管道季节性温度变化为20 ℃。

根据TR-21/2001 塑料管道系统的热膨胀和紧缩标准，在没有任何其他影响的情况下，PE 管道中引起的热应力基于方程式计算如下：

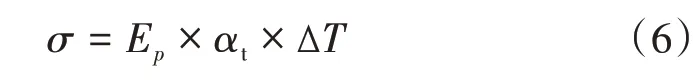
式中：αt－管道热膨胀系数为1/℃；

4 模拟分析

由于经过管道上方的动荷载大小随车辆与管道的水平距离发生变化，加上管道内部气体压力的影响，在内压、外压、温度的共同作用下，管道与修补处均会产生形变，导致管道产生不断变化的应力，我们取每次模拟结果的最大应力（峰值应力）与管道的许用应力进行比较，来评判管道的寿命和修补的效果。本文以管道内压为0.4 MPa 为例，进行模拟计算。

在有限元模型上部设置静荷载与动荷载，在管道端部施加X,Y,Z 约束，施加完成后进入求解器求解，求解完成后进入后处理器显示应力大小与分布，模拟结果如下。

4.1 温度对管道和修补处的影响

埋地管道在不同缺陷尺寸下峰值应力的变化如图5所示。峰值应力在未修补的缺陷管道中随着缺陷部分的加大明显升高，在12.5 mm处高于30 ℃时管子的强度极限，此时聚乙烯管道的寿命急剧减少。而修补过的管道平均峰值应力，即使缺陷直径达到20 mm，管道仍然处于安全范围。从图5 不同温度下应力的变化过程，可以看到聚乙烯管道中的温度降低对热应力产生明显的影响。因此，聚乙烯管道在季节气候温度变化较小的地区更加适用。

图5 不同温度下管道峰值应力随缺陷直径的变化

图6 显示了修补处在不同缺陷尺寸和温度下峰值应力的变化。修补后的峰值应力明显低于许用应力，且随着缺陷孔径的增加增大。与图5 同温度下管道峰值应力比较相差不大，但修补处峰值应力受温度变化的影响远小于管道。在实际修补时，只需考虑温度对管道应力的影响。

图6 不同温度下修补处峰值应力随缺陷直径的变化

4.2 修补形状对管道和修补处的影响

30℃时各种修补形状对峰值应力的影响如图7所示。受损后不进行修补，当缺陷尺寸接近12.5 mm 时达到了许用应力。修补后，缺陷直径达到20 mm，管道峰值应力最高为圆形修补，压力为6.3 MPa，低于7 MPa 的许用应力。修补片中以半圆形和鞍形补片的使用对管道中的峰值应力减小效果最好，对于不同孔径的缺陷，修补效果稳定。圆形修补效果最差，在实际优先采用半圆形和鞍形修补。图8 显示，修补处的峰值应力均满足材料的许用应力。鞍式修复产生的应力最小（4.5 MPa），最大则是半圆形修复（7.5 MPa）。综合图7 与图8结论，单就应力而言，鞍形补片对于修复埋地管中的圆形缺陷更加安全、稳定。

图7 不同修补形状的管道峰值应力随缺陷直径的变化

图8 不同修补形状的修补处峰值应力随缺陷直径的变化

裂缝形缺陷的峰值应力如图9 和图10 所示。通过调整a/b 的数值来模拟管道的断裂程度。图9和图10 模拟了管道和鞍形修补产生的峰值应力随a/ b的变化；未进行修补处理的管道峰值应力一直高于最大许用应力，检测时发现裂缝型缺陷必须尽快处理；当缺陷时形状接近裂缝的形状（a/b＜0.1），管道中的峰值应力超过许用应力的两倍；鞍形修补后，a/b＞0.3 时达到应力要求。对于裂缝形的管道缺陷，理论上当裂缝超比率低于0.3 时，建议直接更换管道。图10 中对于a/b 的变化，修补处的的峰值应力均满足要求，在0.6左右时有最小值。

5 结论

（1）对外径114.3 mm、壁厚10 mm的PE80埋地聚乙烯管道出现缺陷后用PE 进行修补并进行了模拟分析。应用有限元方法模拟了不同形状的贴片修复对埋地聚乙烯管道的应力分布，分析了附加载荷，温度变化，缺陷形状、大小的影响。

（2）管道峰值应力受温度的影响较大。30℃时，当缺陷直径达到12.5 mm管道峰值应力超过最大许用应力，需要进行修补。

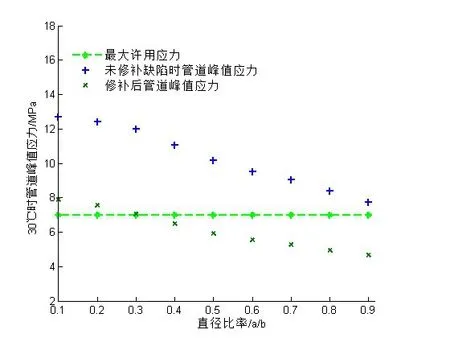
图9 鞍形修补下管道峰值应力随a/b的变化

（3）对于不同修补形状的模拟发现，半圆柱形形和鞍形补片对管道的峰值应力减小效果最好。修补处的峰值应力鞍形修复效果最好。有条件对于圆形缺陷的燃气管道优先使用鞍形修补。

（4）对裂缝缺陷管道，当a/b＞0.3 时，鞍形修补后峰值应力才低于其允许的应力值；当裂缝型缺陷的a/b 比率低于0.3 时，更换管道优先于修补。鞍形修补后修补处的峰值应力呈现抛物线形，在比率为0.6时最佳。

（5）与金属材质管道相比，聚乙烯管道有着更高的热膨胀系数，管道中的温度变化对热应力产生显著影响。因此，埋地聚乙烯更适用于在季节气候变化较小的地区而加大管道埋深亦可降低管道周围环境的温度变化，对减少峰值应力、增加管道寿命有着重要意义。