基于水利水电工程岩质边坡抗滑稳定性分析

王任飞

(锦州市新禹水利工程有限公司，辽宁 北镇 121300)

0 引 言

在重力作用等条件下滑坡体沿软弱面或贯通剪切面向下运动的现象即为滑坡失稳，岩质或土质滑坡为自然界中最常见的灾害类型，大多数边坡因受到地下水、人类活动、地震、生物、附加荷载及岩体成分等因素影响[1]。统计资料显示，在我国山区地质灾害中滑坡对环境的破坏影响最为严重，为实现山区滑坡灾害管理、防灾减灾有必要开展滑坡稳定性研究相关研究，通过对失稳机理、岩体特性的科学分析对于准确预测系统稳定性十分必要[2-4]。

传统的有限元法和极限平衡法为目前岩体边坡稳定性分析的常用方法，经过多年的研究和发展，极限平衡法形成了较为成熟的理论体系并积累了丰富的实践经验，在计算分析边坡可靠度时该方法的应用最为常见[5]。然而将边坡概化为离散的刚性块体集合或连续的均值为该方法应用的基本条件，从而导致结构面控制效应的夸大或未考虑结构面的影响，无法客观、准确的反映随机发育、非贯通结构面的特征，在地层较多且复杂的边坡中不适用。有限元强度折减法和基于滑面的应力分析法为现行的有限元边坡稳定性分析的两类主要方法，其中具有独特优势的强度折减法因缺少明确的失稳判据，在工程实际应用中受到一定的限制；从极限平衡法演变而来的基于滑面的应力分析法，在滑动面上的各参数物理意义明确且应力分析与实际情况更加相符，因此能够准确的搜索到最危险滑动面，便于应用和推广[6]。对于滑移面上基本单元的正应力和切应力该方法通常采用有限元应力代数和比值法计算确定，从而确定总滑动力和总抗滑力的比值。然而，对各滑面上的力进行代数和相加不适用于滑裂面间存在方向夹角的情况，这有悖于力学原理。

综上分析，文章在第三滑裂面上通过转换计算各滑裂面上的剩余力提出有限元剩余推力法，通过对比分析传统的应力代数和法计算结果，验证了该方法的可靠性与准确性，可为边坡的加固处理及其破坏模式的预测研究提供一定的理论依据。

1 有限元剩余推力法

传统的边坡稳定分析及其与有限单元法之间的关系研究相对较早，其主要工作是将潜在的滑裂面引入至边坡稳定中，然后对滑裂面上各点的应力按照有限单元法获取的应力进行计算，其中安全系数按照加权平均的原则确定[7]。工程实践表明，在弹性状态下确定的有限元安全系数十分接近于极限平衡法[8]。对此，为确定一个临界滑裂面许多研究者做了进一步的研究，所获取的临界滑裂面和最小安全系数比较接近于极限平衡法，且二者的计算流程基本相似。

采用有限元进行计算时选择岩块、节理分别作为滑体变形和强度的参数，若将安全可靠性最低的坡面作为滑裂面，则该条件下的抗滑力和滑动力之比即为安全系数K，通过对应力的积分计算确定滑动力和抗滑力。为了求得各个单元上的应力状况应先将目标结构体离散化呈四边形基本单元，然后对单元内任意斜截面上的切应力、正应力利用有限元法进行计算，其表达式如下：

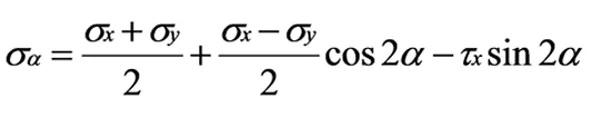
(1)

(2)

式中：τα、σα分别代表各单元斜截面上的切应力和正应力；σx、σy分别代表沿水平和竖直方向上单元的正应力；α、τx分别代表斜截面水平方向与外法线之间的夹角、基本单元受到的切应力。

计算简图如图1所示，在倾角为α、β的两条软弱结构面上分布有第一、第二滑裂面AB和BC，与水平方向成θ夹角的第三条滑动面为CD，滑落体自重为G。为搜索安全系数最小的滑裂面可改变水平方面与第三滑裂面之间的夹角，即确定最危险滑裂面，滑动力和抗滑力在第一、二、三滑裂面上一次为τ1、σ1、τ2、σ2、τ3、σ3。

图1 计算简图

材料的摩擦系数和初始黏聚力在安全系数K值为1时分别为f=f/K、c=c/K，则经过n个单元的所有斜截面上的应力代数和即为第一滑裂面上的滑动力τ1、抗滑力σ1，计算式如下：

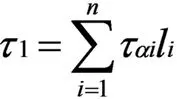
(3)

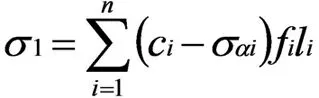
(4)

式中：ταi、σαi分别为第i单元的α斜截面在第一滑裂面的切应力与正应力；ci、fi分别为第i单元的黏聚力和摩擦系数；li为α斜截面在第i单元上的长度。

根据下述计算公式确定剩余力R1在第一滑裂面上的值，即：

R1=α1-τ1

(5)

在R1值为正的情况下，则剩余力在第一滑裂面上为推力，采用公式T1=R1cos(α+θ)转换计算至第三滑裂面上的推力；在R1值为负的情况下，则剩余力在第一滑裂面上为抗滑力，采用公式Z1=|R1cos(α+θ)|转换计算至第三滑裂面上的阻力。同理，可求解剩余力在第二滑裂面上的数值。采用如下计算公式确定安全系数在第三滑裂面上的数值，即：

(6)

式中：M1、M2分别代表剩余推力、阻力在第一、二滑动面上之和。

通过对比分析初始K值和所求得的K值，若满足计算精度要求则计算结果即为最终的安全系数；否则，应重新迭代计算，直至符合计算精度要求。

2 实例分析

辽宁省某水利水电工程主要由蓄水库和水利设施机组构成，上、下水库之间主要由永久道路连接。岩体边坡的地震加速度为0.05g，抗震设防烈度为6°，有高速公路、城镇居民等建设用地分布于上游边坡地区，库区沿线岩质边坡受荷载、风化等影响强烈且岩体松动边坡较多，两条非贯通软弱结构面分布于倾角为45°的岩体边坡内，软弱结构面自上而下的倾角依次为56°、20°，一旦发生失稳滑坡，不仅严重威胁着过路车辆与工作人员的安全，而且对水库河流造成严重的水体污染。对稳定性利用文中所述方法进行对比分析，边坡的材料力学参数见表1。

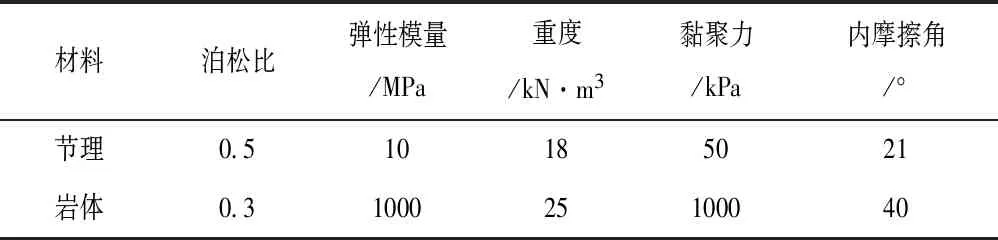
表1 基于有限元法的岩体及结构面材料参数

对边坡的抗滑稳定性分别采用有限元应力代数和法与剩余推力法进行求解计算，结果见表2。

表2 基于不同角度的安全系数计算值

根据表2可知，随第三滑裂面角度的变化应力代数和法计算得到的K值表现出单调递减趋势，该变化趋势与工程实际不符；随着角度的变化剩余推力法求解的安全系数呈现出先减少后增大的变化特征，该变化特征与实际工程保持一致。

基于剩余推力法搜索到的最危险滑裂面发生在第三滑裂面与水平方向夹角为29.5°处，所对应的K=2.600，在同等条件下应力代数和法计算得到的K=3.30，由此可见剩余推力法具有更高的科学准确性。进一步分析其原因为应力代数和法未考虑滑裂面角度的影响，只是将各滑面上的力进行简单的相加得到的安全系数不准确；而考虑了各滑裂面间夹角对力传递影响的有限元剩余推力算法，计算得到的边坡安全系数更加符合工程实际情况。

随第三滑面与水平方向夹角θ的改变剩余推力法求得的边坡安全系数K的变化规律如图2。根据图2可知，剩余推力算法求得的K值在竖直和水平滑裂面上很大，岩体边坡结构稳定，该方法能够确定安全系数最小值。随着夹角θ的增大应力代数和法求得的边坡安全系数K呈减小趋势，K值在竖直滑裂面上最小，该变化特征与实际情况相违背，因此基于剩余推力算法求解的安全系数更加能够反映工程实际情况，具有较好的科学合理性。

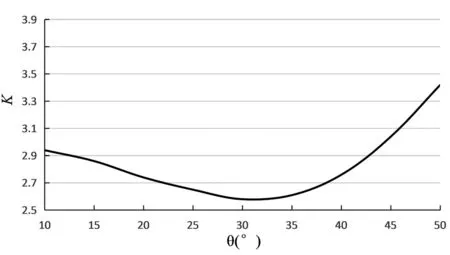
图2 夹角θ与K值的变化关系

3 结 论

文章在第三滑裂面上通过转换计算各滑裂面上的剩余力提出有限元剩余推力法，通过对比分析传统的应力代数和法计算结果，验证了该方法的可靠性与准确性，得出的主要结论如下：

1)考虑安全系数受滑裂面间夹角因素的影响作用，在传统的应力代数和法的基础上提出有限元剩余推力法，对最危险滑裂面采取改变滑裂面倾角的方法确定。

2)工程实例表明，较传统的应力代数和法计算结果有限元剩余推力算法能够更加符合工程实际情况。所以，较应力代数和法计算边坡稳定性剩余推力法更加科学可靠。