基于点线特征鲁棒性评估的双目视觉里程计

荣燊

（合肥工业大学电子科学与应用物理学院 安徽省合肥市 230009）

同步定位与地图构建（Simultaneous Localization and Mapping）即SLAM 技术，在自动驾驶、无人机控制以及太空机器人等自动化领域应用广泛，主流的视觉SLAM 大致分为三类：基于滤波器[1]、基于关键帧优化[2-4]、基于直接跟踪的方法[5-7]。而作为视觉SLAM的前端视觉里程计，为后端估计出一个较为准确的位姿是其主要的工作。

基于点线特征的视觉里程计[8-10]位姿估计的精度依赖点线特征匹配的精度，传统综合特征的视觉里程计对提取出的特征匹配，采用最小化3D-3D 误差[11]或3D-2D 误差[9]对方法对位姿进行估计。这些方法把提取出的所有特征匹配的精度视为一致的，对这些匹配的特征建立单一误差模型，求解相机的位姿。考虑到在双目立体匹配中，由于匹配的特征点的视差越大，三角测量的不确定性越小，估计出的特征点深度精度越高，但是视差越大的匹配点的深度越低，在特征跟踪时容易丢失，且匹配的可靠性较差，这就形成了三角测量精度与特征点匹配精度相矛盾的地方。

本文综合考虑匹配精度和三角测量精度，提出一种特征鲁棒性估计方法，通过筛选鲁棒性高的特征点和特征线段，综合计算效率，提出了一种结合了ICP和PnP方法估计位姿的点线双目视觉里程计，并在KITTI-ODOMETRY 公开数据集上通过与PL-StVO[9]对比，验证了本文算法的有效性。

1 算法框架

本文视觉里程计算法框架如图1 所示，分为位姿估计、关键帧选取、局部建图三个部分。其中，位姿估计是本文的算法的核心工作。

特征提取过程中，本文使用了ORB[12]进行特征点提取和描述，LSD[13]进行特征线段提取并采用LBD[14]描述子进行描述。通过对提取的特征线段长度进行约束，过滤场景中大多数非结构化直线，减少线特征描述子的计算成本，对特征线段采用端点模型表示，简化特征线段的处理方式。并通过对特征点线进行极线约束，进一步提高特征匹配的精度。通过对KITTI 数据集[15-16]中双目图像对特征匹配对的视差统计，结合双目视差对三角测量不确定性的影响，对特征点进行鲁棒性评估，对三角测量精度高的特征点认为鲁棒性较高，计算特征点深度，作为3D 特征内点；对三角测量精度较低的特征点，认为其三角测量误差较大，作为2D 特征内点，将特征点分为3D 和2D 特征。在帧间跟踪时，针对3D-3D、3D-2D、2D-2D 不同的特征匹配，提出了结合ICP 和PnP 方法的位姿估计方法。最后进行选取信息冗余度低，位姿估计精度高的关键帧进行局部地图优化。

图1：算法框架

图2：在KITTI_00 序列上使用LSD 提取直线的结果

2 双目视觉里程计

2.1 特征提取和匹配

由于SLAM 系统的实时性要求，本文方法采用ORB 方法对特征点提取和描述，采用LSD 方法对特征线段进行提取，采用LBD方法对特征线段描述。

LSD 特征提取是一种基于区域生长的线段提取算法，在提取时会检测到许多细小的线段，如图2 所示，这些线段数量庞大，而且大多数非图像中的结构化线段，带有较大的不确定性，且对数量庞大的线特征计算描述子会耗费更多的计算成本，导致算法效率下降。本文首先通过对检测出的线特征几何长度进行约束，去除这些非结构性线段。

算法流程如下：

（1）对图像首先采用梯度密度滤波器[17]进行预处理，剔除如图2.1 中所标识出来的密集区域，然后采用LSD 算法进行线段提取；

表1：本文方法和LBD 描述子描述和匹配平均每帧耗时对比（ms/帧）

（2）计算所提取线段的LBD 描述子，进行特征匹配，并采用RANSAC 方法对特征匹配中的误匹配进行预剔除；

（3）对成功匹配的特征线段使用端点模型表示，提取端点和线段中点进行极线约束，只要有一个点满足了极线约束，则认为该线段特征匹配成立。

本算法第一步是为了对线特征进行粗筛选，减少计算细小线段所带来的计算量，这些细小的线段往往非刚体结构，易受环境变化而变化，会给匹配带来更大的误差和更多的计算量，所以在粗筛选中直接剔除；第三步极线约束采用端点三选一策略是为了防止检测到的存在局部遮挡的线特征被极线约束过滤。

本算法使用的测试平台如下：CPU 为Intel（R） XEON（R） CPU E3-1231 v3 @ 3.4GHz，内存为8G DDR3 1600MHz，测试系统为Ubuntu16.04。对KITTI-ODOMETRY 的00-10 这11 个双目序列使用单一线程对本算法进行时间统计，与直接使用LBD 计算描述子所用的时间对比结果如表1 所示。

实验证明本文方法与直接使用LBD 描述子相比在KITTI 00-10的所有数据集上的速度均更快，平均耗时大约仅为直接使用LBD描述子的25%左右。

2.2 特征内点筛选

通过极线约束可以初步筛选出匹配精度较高的特征内点，这些特征内点以它们各自在对应图像中的二维像素坐标的形式储存，需要对这些匹配特征内点通过三角测量，求出它们所对应的空间3D点坐标。但是由于数字图像的分辨率是由像素决定的，在相机基线一定的情况下，三角测量的不确定性将由匹配点的视差决定。

本文以KITTI-ODOMETRY 公开数据集中使用的相机的内参数矩阵为例，利用计算出视差沿逐个像素增长时深度估计的区间宽度。如图3 所示，可以很明显的看出随着视差值的增加，三角测量的不确定性也在大幅下降，当视差大于20 个像素时三角测量估计出的深度误差已经在1 米以下,当视差大于100 个像素时，三角测量的深度误差已经降到1%以下。但是在双目匹配中，视差值较大的特征点其深度值较小，在相机运动时容易丢失，且有可能是误匹配的特征，保留所有视差较大的特征匹配会引入误匹配的特征点，三角测量将没有意义。

本文通过对KITTI 00-10 这11 个序列中每个序列均匀抽取100帧立体图像对，进行特征匹配和极线约束，一共筛选出133273 对匹配的特征内点进行视差统计，绘制直方图如图4 所示。考虑到位姿估计时，多次迭代所需要的最小特征点数量，发现大约54%的特征点的视差的绝对值聚集在[0，200]这个区间内，平均每帧有66 个特征点。由于三角匹配和特征匹配的要求互相矛盾，首先考虑满足特征匹配的要求，建立准确的特征匹配是估计相机位姿重要的一步。首先对极线约束的视差进行分割，选择视差的绝对值范围在[100,200]之间的图像特征点，其三角测量误差较小，约占特征内点总数的22%，平均每帧有27 对可靠的3D 特征内点匹配对；视差的绝对值范围在[20,100)之间的图像特征点，其三角测量得出的深度值误差较大，认为三角测量不可靠，大约占特征内点总数的25%，平均每帧有30 对可靠的2D 特征内点匹配对；对视差范围在200 以外的特征点，其深度值过小，在相机运动时容易丢失，且特征匹配的可靠性较低，将其从特征内点中移除。

图3：双目视差与三角测量不确定性

图4：极线约束视差统计直方图

2.3 结合ICP和PnP的位姿估计方法

图5：00（a）、01（b）、08（c）、10（d）四个序列的相机轨迹对比

估计相机位姿是视觉里程计最重要的工作之一。视觉SLAM后端的优化效果在一定程度上取决于前端视觉里程计给定的初始值，前端如果能在保证算法实时性的基础上估计出一个良好的初始值给后端，可以减小后端迭代优化算法的计算成本，提高后端优化的精度。

通过三角测量和特征鲁棒性评估，筛选出了通过三角测量估计出特征点的空间位置，对这些特征匹配点进行分析，发现在帧间匹配时会出现以下几种情况的匹配：

（1）3D 特征内点与3D 特征内点（3D-3D）的匹配；

（2）3D 特征内点与2D 特征内点（3D-2D）的匹配；

（3）2D 特征内点与2D 特征内点（2D-2D）的匹配；

考虑2D-2D 特征内点之间由于深度不确定性较大，通过2D-2D 特征内点估计位姿时没有深度信息的约束，导致估计时相机的位移t 误差较大。所以本文对2D-2D 匹配的特征内点不进行位姿估计，直到它们重新与3D 特征内点建立匹配。

对3D-3D 匹配的特征点建模它们的三维世界坐标误差：

李代数上的扰动为：

表2：KITTI 数据集不同序列的平均轨迹误差（%）和旋转误差（deg/m）

对3D-2D 匹配的特征点建模它们的重投影误差：

李代数上的扰动为：

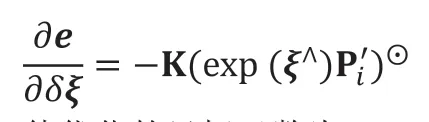
待优化的目标函数为：

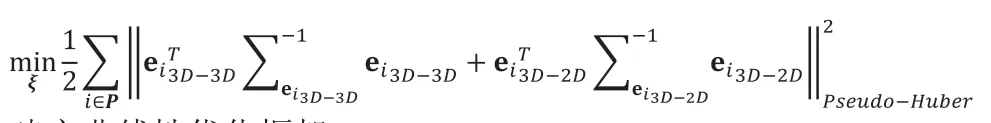
建立非线性优化框架：

（1）给定初值ξ0

（2）对于第k 次迭代，求解

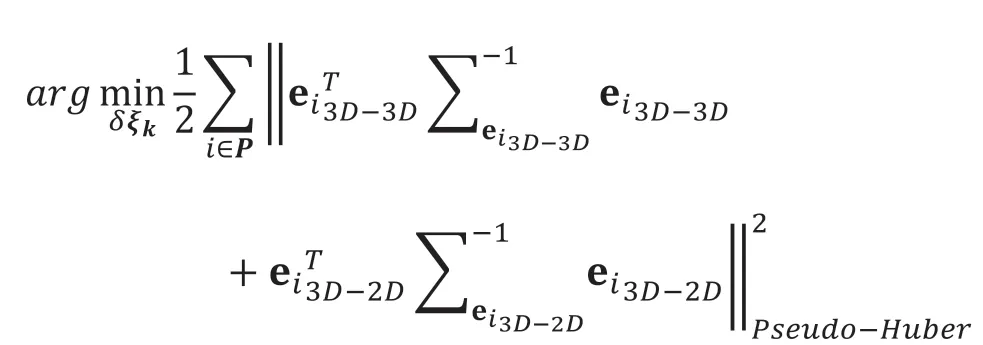
（3）若δξk足够小，则停止，否则，返回第二步。

其中，本文采用匀速运动模型使用上一帧的相机位姿ln(exp(Δ ξ^) exp(ξ^))⋁对ξ0进行赋初值，采用Pseudo-Huber 鲁棒核函数减少误差过大的特征对位姿估计的影响，并对参与位姿估计的特征内点数量进行统计。

2.4 关键帧选择

在相机运动过程中采集到的数据规模会随着时间越来越大，而且不同时刻相机采集到的图像质量也参差不齐，将每一帧图像所估计出的相机位姿均作为后端优化的状态会导致地图规模迅速扩大，后端优化的成本也会急速增长，导致后端效率低下，因此需要从整个图像序列中挑选一些有代表性的图像作为关键帧。关键帧的选取极为重要，它包含了整个系统所维护地图的大多数数据，对于系统精度和效率的影响极大。关键帧挑选的过于密集，会导致后端计算效率过低，地图维护成本过高；关键帧挑选的过于稀疏，会导致关键帧之间的位姿估计误差较大，帧间匹配困难，甚至导致跟踪丢失。

结合ICP 和PnP 的位姿估计，可以为后端估计出相机的初始位姿，但是这些初始位姿的不确定性，需要对其定量分析。根据文献[14]，本文采取了将相机的相对位姿估计的不确定性从协方差矩阵转化为熵：

然后，对于上一个最近提取的关键帧i，需要检查第i 帧的熵与当前帧i+u 的上的比值：

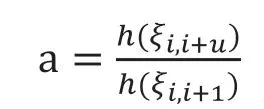
如果a 的值低于设立的阈值，那么就认为新帧带来的不确定较多，需要将当前帧第i+u 帧加入关键帧。本实验中，阈值将设为0.9。

于是本文所采用的关键帧选择需满足以下所有条件：

（1）距上一次关键帧插入已经间隔超过n 帧或局部建图线程空闲，n 取决于序列总长度和相机运动速度；

（2）当前帧至少筛选出50 对特征点和10 对特征线段；

（3）当前帧熵与上一个关键帧的熵的比值大于0.9。

其中条件2 确保了当前帧作为关键帧时位姿估计的精度，条件3 保证了两个关键帧之间由于新信息的引入而导致的不确定性的增长，代表了两个关键帧之间必定要有一定的不相关。

3 局部地图构建

本文通过将关键帧加入局部地图，通过对局部地图中关键帧之间描述子的匹配关系，建立关键帧之间的共视图，即局部闭环，对共视图中的关键帧及其对应的路标点进行光束平差法优化消除局部累积误差，获得局部精确的关键帧位姿。

4 实验结果分析

为了保证本文提出系统精度、效率的可对比性，本文的系统在KITTI 公开数据集上进行测试。KITTI 数据集由德国卡尔斯鲁厄理工学院和丰田美国技术研究院联合创办，是目前国际上最大的自动驾驶场景下的计算机视觉算法评测数据集[15-16]。本文选取文献[9]中不含后端闭环的PL-StVO 与本文提出的视觉里程计位姿估计的结果进行对照，在给出了真实轨迹和位姿的KITTI 公开数据集的00-10 这11 个序列上进行对比。

本文对于每一次实验，通过比较本文算法和PL-StVO 算法对相机轨迹和位姿的估计值和实际值之间的误差来衡量估计轨迹的全局一致性，如图5 所示，给出轨迹对比较为明显的00、01、08、10四个序列的对比效果。在图5 中可以较为明显的看出与PL-StVO对比，本文算法的相机轨迹精度更高。这是由于在观测值误差噪声较小的情况下，最小化帧间跟踪的特征匹配对的3D-3D 误差具有最优的封闭解，在存在唯一解和无穷多解的情况下，求出的局部极小值即为全局最优值，不会出现局部极小而非全局最小的情况。

为了量化算法精度，本文采用KITTI 公开数据集所提供的里程计开发工具分别对本文算法和PL-StVO 进行评测。评测结果如表2所示。

对比PL-StVO，可以看出在平均轨迹长度上本文算法估计出的平均相机轨迹误差在00、01、02、03、04、05、07、08、09、10 序列上均比PL-StVO 要好,估计出的平均相机旋转误差在00、01、03、04、05、07、08、09、10 序列上要优于PL-StVO。在平均相机运动速度上本文算法估计出的平均相机轨迹误差在00、02、07、08、09、10 上要优于PL-StVO，估计出的平均相机旋转误差在00、03、06、08、10 等序列上均优于PL-StVO，证明了对相机轨迹的估计精度和对相机位姿估计的精度都有一定提升。这是由于本文算法对特征匹配中的特征对进行鲁棒性分析，在保证匹配精度的同时筛选出三角测量精度更高的特征匹配，通过对它们对应的空间点建模3D-3D 误差，对鲁棒性较差的特征匹配建模3D-2D 的重投影误差，提高了精度更高的观测点的对位姿估计的影响，所以提高了相机位姿估计的精度。

5 结论

本文的主要贡献包括：

（1）在前端视觉里程计中针对线特征，利用了线段的几何信息改进了LBD 描述子的匹配过程，考虑了线段易受不同程度的遮挡，采用端点模型三选一极线约束的方式完成匹配。

（2）综合考虑点线特征的匹配过程中特征匹配的精度和三角测量不确定性之间的矛盾，提出特征鲁棒性评估，根据三角测量精度划分不同鲁棒性的特征。

（3）改进了位姿估计的计算方式，通过对3D-3D 匹配的特征内点建模空间点位置误差，对3D-2D 匹配的特征内点建模重投影误差，重写优化函数，并通过非线性优化的方式估计位姿。

（4）改进了新的关键帧选择策略及地图更新方式，提高了选择的关键帧的精度，避免了关键帧的冗余，使其在后续的局部建图和闭环检测及校准过程更为高效。