融入情境信息的矩阵分解个性化推荐模型

刘铮

（辽宁大学信息学院 辽宁省沈阳市 110000）

随着互联网技术的高速发展个性化推荐系统的出现成为解决信息过载有效工具，其中矩阵分解模型具有很好的可扩展性和预测精度。然而目前基于矩阵分解模型的个性化推荐方法大多没有充分融合情境因素。

推荐系统在实际应用中，用户和项目在不同的情境环境下应该有差异化的评分表现。Xiang[1]等人考虑到用户兴趣及项目热度可能会随时间而衰减提出了TimeSVD。Baltrunas[2]等人提出了一种在偏置项中融合情境信息的矩阵分解模型。现有矩阵分解推荐模型的精度有待提高。本文提出了一种融入情境信息的矩阵分解推荐模型，针对前人模型的缺点做出了相应改进。

最后通过实验进行对比分析验证改进后模型在控制均方根误差方面提升明显，有效提高了推荐准确率。

1 情境感知推荐技术

情境感知推荐技术是情境感知推荐系统的核心，融合与处理了各类情境信息分为情境预过滤、情境后过滤、情境建模等三种情境感知推荐技术。

1.1 情境预过滤

情境预过滤：该技术主要思想是根据情境信息对原始数据进行预处理，仅保留满足特性情境的数据。

1.2 情景后过滤

该技术的主要思想是在生成预测值阶段不需考虑情境信息，其后根据特定的各类情境条件，对推荐结果进行筛选过滤.

1.3 情境建模

该技术的主要思想是将情境信息直接融入整个推荐过程，将情境信息视为用户历史行为数据外的若干维度，建立相应模型进行用户个性化推荐。

2 引入偏置项的隐语义模型

隐语义模的主要任务就是将矩阵R 分解为矩阵P 和矩阵Q 的乘积，然后利用P 和Q 的乘积预测用户对项目的兴趣度，加入了偏置项的隐语义模型如公式（1）所示：

其中，μ 表示评分的平均值；bu 表示用户u 的评分基线；bi 表示项目i 的评分基线，pu 和qi 分别表示用户u 和项目i 在同一个隐含空间上的向量，puTqi 乘积表示和原始稀疏评分矩阵近似的矩阵。

3 融入情境信息的矩阵分解推荐模型

3.1 情境信息处理

模型引入用户-项目-情境信息之间交互时可分为三部分计算：用户-项目之间交互、用户-情境之间交互以及项目情境之间交互。将用户、项目及每个情境条件映射到一个共同的D 维潜在因子空间，用相同维数的因子向量分别表示用户、项目及每个情境条件。因此用户及项目与情景变量的交互可以用其分别的因子向量的内积来计算。

表1：模型学习过程

在给定的训练数据集R 中，给定一个训练数据集，包含k 个情境变量，每个情景变量具有多个情境条件。其中第L 个情景变量用cL 表示，L=1，2，3，…k，cL=0，1，…zm。其中cL 的值表示具体的情境条件。

接着本文用ruicl...ck 来表示已获得的用户u 在情境c1....ck 的条件下对项目的评分，而用户在相同情境条件下的预测评分用来表示。

基于此，融入情境信息的矩阵分解推荐模型形式化描述如公式（2）所示：

其中cu 表示用户u 因情境信息的影响而产生的评分偏差；ci表示项目i 因情境信息影响而产生的评分偏差，α 和β 分别表示上下文信息对用户和项目的影响程度，即用户和项目对情境信息的敏感度。puTcl 与qiTcl 分别表示用户及项目与情境变量cl 的交互计算。

电动汽车行驶每小时耗电2kWh，充电站充电功率为10kW，效率为1。充电站A、C、D、E的预期电价以及目标函数α/β如表1中所示。分时电价制度按峰时每kWh为2.00元，谷时每度1.00元计算。

3.2 偏置项改进

本文模型选取时间因素作为对偏置项改进的切入点。

其中δ 为时间衰减常数。

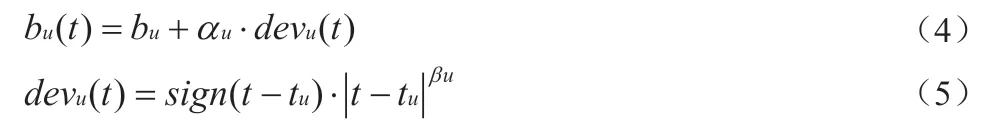
其中tu 为用户评分时间均值，βu和αu通过交叉验证来设置。

3.3 模型求解与推荐

为了求得模型最优解，从而得到预测值。我们设置损失函数如公式（6）所示。

采用随机梯度下降法SGD 求解各参数，通过求各参数的偏导数找到最速下降方向，以得到模型的最优解，从而得到预测评分[12]。模型学习过程如表1 所示。

利用训练好的矩阵分解模型预测用户对项目的评分值，在预测完项目评分之后采用Top-N 方式生成推荐列表。

4 实验

4.1 实验数据及评价标准

本文采用的是LDOS-CoMoDa 数据集[4]，该数据集的数据来自用户观影后对电影的评分，并包括了相关的情境信息，共有12 个情境维度随机抽取数据集中的10%作为测试集，其余90%为训练集，随机抽取产生的测试集和训练集。本文选取的对比实验模型分别为张量分解模型，TimeSVD[3]模型，及CAMF-C[4]模型。

在实验中采用RMSE（均方根误差）作为模型优劣的评判标准，如公式（7）所示。

4.2 实验结果与分析

本文实验选取的数据中，有12 个不同的情境维度，其对于推荐结果影响不同，选择合适的情境信息加入模型，本文使用WEKA[5]软件实现情境变量的选择。

在本文实验中，首先在实验集上根据传统的矩阵分解模型LFM 进行多次迭代训练，得到模型的最优参数值。分别取隐类空间D=10，学习速率η=0.02，正则化参数λ=0.01，最大迭代次数为50。然后本文所提模型设置同样的参数，并手动调整用户和项目的全局情境敏感度可知，α=0.1，β=1.9 时模型达到最优解。

为了选择适当的情境变量加入模型，本文研究了在引入不同数目的情境信息下，模型均方根误差最优值。在本文模型中加入信息增益值前五的情境变量时，可令模型取得最小RMSE 值。

本文选取基于张量分解的推荐模型MR，timeSVD 模型以及改进情境偏置项的CAMF-C 模型与本文提出模型ICMF-T 在LDOSCoMoDa 数据集条件下进行对比实验。得到实验结果如图1。

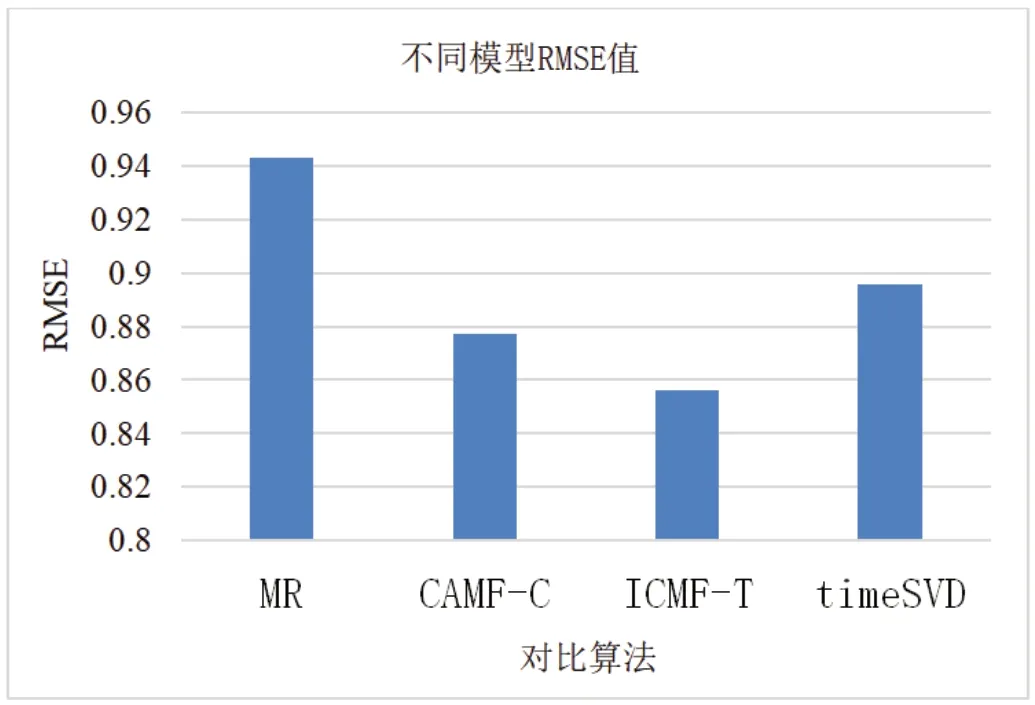
图1：各模型RMSE 值

由图1 可明显得到在多情境变量的数据集条件下，本文提出的融合情境变量的改进矩阵分解模型（ICMF-T）在均方根误差方面具有明显提升。

5 结束语

本文为了解决传统矩阵分解模型中未充分利用情境信息而造成的准确率不高等问题，提出了一种融入情境信息的矩阵分解个性化推荐模型。在充分利用各情境信息与用户和项目交互以提高推荐精度的前提下，尽可能降低因冗余情境维度造成的噪音污染。利用用户和项目敏感度用以平衡因各用户和项目对不同情境维度的敏感度不同而造成的推荐结果偏差，通过在具有多情境维度的专家评分数据集中与其他广泛应用的矩阵分解模型做实验对比，本文所提模型在控制均方根误差方面具有明显优势，推荐效果良好。