基于SVD高职院校在线教学资源推荐系统

林海

(惠州城市职业学院 广东省惠州市 516000)

推荐系统的应用涉及多个行业，比如电商、新闻、餐饮、旅游等。但传统高职院校，建立的在线教学系统，侧重于管理功能。学者对推荐系统的应用研究主要聚到商业与工业。如黄玲（2020）基于云平台的电子商务智能推荐系统的研究[1]；李家华（2019）基于大数据的电商导购平台研究[2]；李太松等（2019）基于循环实际卷积网络的序列流算法的研究[3]；王婧虹（2019）基于用户特征的在线酒店推荐技术研究[4]。至于推荐系统存在的问题，学者做了大量的研究，如李振波等（2019）基于协同回归模型的矩阵分解推荐研究[5]；陈晔等（2018）对LFM 矩阵分解的推荐算法优化研究[6]；叶俊民等（2019）推荐算法中运用了НIN[7]；梁丽君等（2018）运用K-means聚类算法对用户属性特征进行聚类的研究[8]。学者们的研究既有传统推荐方法的改进、亦有深度学习、机器学习等新兴方法的引入。涵盖了SVD、多元混合、EGE 模型、张量填补、联合推荐、协同回归、LSTM、FuckSVD、Apriori、三支交互、深度神级网络、知识图谱、专家推荐、隐语义分析、二分网络、TLRank、上下文推荐、社会化推荐等。

对于学习系统(在线教学资源系统)的推荐，学者做了一定的研究，或重点聚焦技术，或重点聚焦用户行为持续使用因素等，如曹斌等（2015）研究了在线书籍用户阅读时间与频次融合的推荐方法[9]；张颖（2016）探讨了云计算中的学习资源个性化推荐[10]；夏立新等（2018）探讨了布尔型移动在学习资源推荐系统的应用[11]；徐雪珂等（2019）算法研究了个体特征和教学评价[12]；张娅雯等（2020）在移动学习平台用户使用意愿影响因素研究，基于移动情境和心流体验的技术接受模型[13]；未来,对个体特征更深入的探究、基于教育本质的跨学科多元融合、新兴技术和产业发展前沿、差异性环境等将赋予影响因素研究更为丰富的内容。

在高职院校在线教学资源系统中，推荐系统会面临如下问题：

（1）数据稀疏。高职学生之间的交集可能很小，使得高职学生之间的关联性很小。

（2）准确率低。高职学生甚少主动去对课程进行评价与评分，如果运用简单的方法去补缺失值，造成准确率严重偏低。

高职院校的教务系统、招生系统、就业系统等保存了学生相对完善的历史数据。高职学生的年龄、性别、专业、年级、成绩、选课记录等数据是相对客观与完善的。此类数据，在构建高职学生对教学资源兴趣偏好中的权重如何设置？如何用SVD 技术解决在线教学资源评分数据的缺失？高职学生对课程兴趣偏好特征模型如何构建？高职课程的特征模型如何构建？如何以较小的运算代价去实施推进？是需要解决的问题。

1 相关工作

1.1 国外对推荐系统的研究

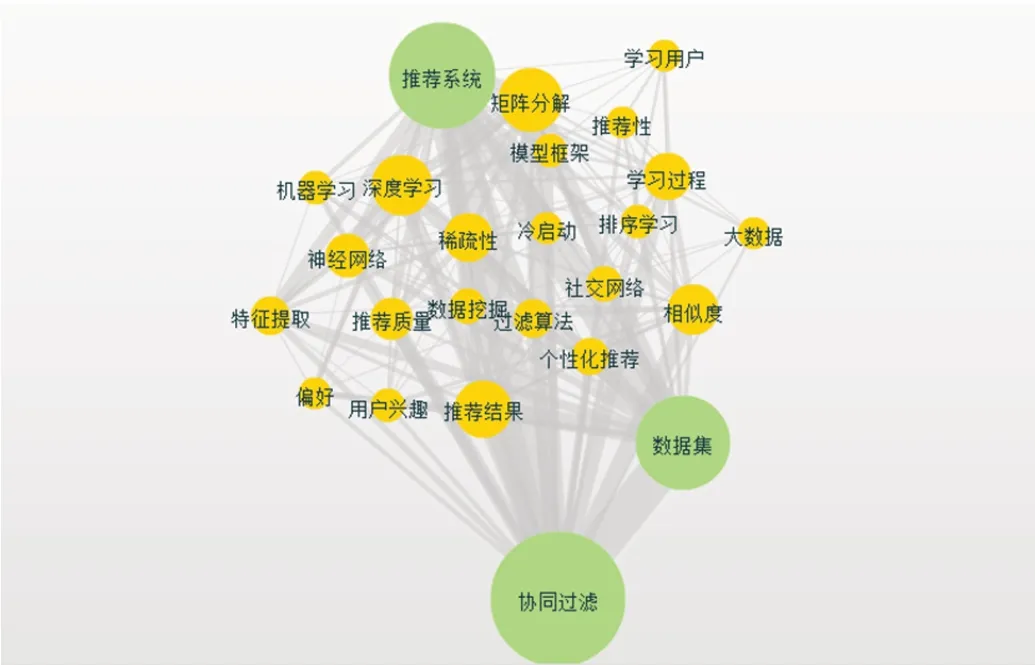
图1：知网收录推荐算法2015-2020年关键词共献网络图

Goldberg 等(1992)提出基于用户的协同过滤算法；面向项目的协同过滤算法由亚马逊(2001)提出；国外学者在推荐系统研究的理论及模型的研究较多，如由个性化导航系统Armstrong(1995)等提出；Нerlocker 等(2007)人提出通过其他人的意见过滤或评估项目的过程，支持过滤大量数据；Cho 等(2002)提出了基于Web 使用挖掘和决策树归纳的个性化推荐系统；McDonald 等(2000)提出了专家推荐；基于协同过滤的推荐系Web 服务由Zheng 等(2009)提出；Linton(2000)提出了一种面向组织学习的推荐系统；Нe(2010)提出基于社交网络的推荐；Luo(2012)提出了基于正则矩阵分解的增量式协同过滤推荐；Нofmann(2004)提出了潜在语义模型的协同过滤推荐;Engle(2011)提出了基于属性分析的协同过滤系统及方法。

推荐系统的评估主要有统计精度方法、决策支持方法。其中，统计精度方法比较常见的为平价误差、均方根误差。另外还有召回率、准确率。其评分预测准确度能够通过RMSE 计算。其公式定义如下：

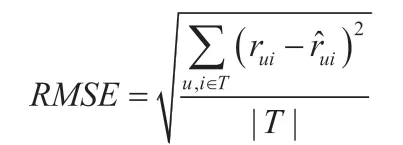
MAE 的计算公式为：

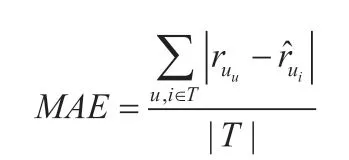
训练集中推荐列表用Y(a)表示，是用户在测试集上的行为列表用Q(a)表示，召回率的计算公式为：

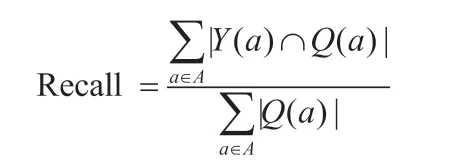
准确率的计算公式为：

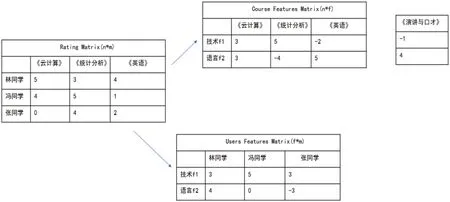
图2：SVD 推荐思维图

1.2 国内对推荐系统的研究

国内在推荐系统的研究，以知网调研为例，2015年-2020年知网收录以“推荐算法”为主题的核心期刊有1241 篇。其中2015年为184 篇、2016年为230 篇、2017年为224 篇、2018 为279 篇、2019年为269 篇、2020年预测为303 篇。主题分布主要集中在协同过滤、推荐系统、目标用户、相似度、矩阵分解、人性化推荐、用户偏好、冷启动等。加上主题“学习”，搜索到101 篇核心期刊文献、在关键词共现网络中，将节点过滤频次设置为4 次。关键词共现网络主要为推荐系统、矩阵分解、数据集等。如图1 所示。

国内学者比较集中在推荐系统的应用层面的研究，比如王晓东等（2018）基于知识表示和协同过滤,将学习者的学习水平和学习风格等特征融入推荐过程；卢春华等（2019）基于有限的领域特征,在目标领域和训练领域之间建立了一个基于特征相似度的桥梁；查英华等（2015）以高职学生的学习特征为基础，运用了上下文推荐等来实施；王光等（2019）计算用户相似度矩阵融合了用户属性；付芬等（2018）通过收集用户的学习行为，改进传统的相似度计算方法；李散散（2019）提出了出基于用户行为分析和LDA 模型的数字媒体推荐系统；李昆仑等（2020）实施融合项目和用户隐式反馈构建系统；熊回香等（2019）利用了Word2vec 构建推荐系统；胡思才等（2019）运用了神经网络和概率矩阵分解构建推荐系统。

综上，国内外对商业类的推荐系统的研究比较多，包括推荐系统、矩阵分解、数据集等。但对于高职院校在线教学资源的推荐系统的研究与实证较少。

2 SVD奇异矩阵分解

基于SVD 或SVD 组合实施推荐的研究是比较流行的选择，如刘晴晴等(2019)混合推荐算法利用SVD 来填充；吴进等（2019）实施Lasso 回归与SVD 融合的算法；苏庆（2019）引入时间效应的SVD++线性回归推荐算法的研究；邢长征等（2018）基于SVD++与标签的跨域推荐模型的研究；可以得知SVD 算法因其特殊优点而得到广泛应用，因此，本次研究采用SVD 为基本方法。

2.1 SVD推荐思维

SVD 的基本思想是用3 个小矩阵来描述较为复杂的矩阵。SVD的推荐思维示例，如图2 所示。

（1）Rating Matrix、Course Features Matrix、User Features Matrix 三个为评分表。其中Rating Matrix 表示3 个同学对3 门课程的评分，可以看出冯同学对《统计分析》的评分为5，对《英文》的评分为1。

（2）假如我们打算给冯同学推荐《演讲与口才》这门课，但冯同学只有前面3 门课程的评分。无法直接得出冯同学是否喜欢《演讲与口才》课程。这个时候，需要对冯同学对课程类型喜欢的程度进行判断。引入SVD 来解决这个隐语义问题。

（3）定义课程类型的程度与类型偏好程度，例子中采用的两个程度分类，分别是技术类、语言类。Course Features Matrix 中给出每门课的程度值，《统计分析》5 分，高度输入技术类课程，但非常不属于语言类课程，得分为-4 分。User Features Matrix 的表示每个同学对于课程类型喜欢的程度，比如冯同学最喜欢技术类课程，但不喜欢语言类课程。

（4）计算课程类型程度与类型偏好程度的点积。以冯同学为例，将User Features Matrix 表中对应元素与Course Features Matrix 表中对应的元素点积，选取《统计分析》得到的点积为25，选取《英语》得到的点积是10，用点积数值表示冯同学对《统计分析》、《英语》的喜欢程度，可以得出更加喜欢《统计分析》。如此，可以得出每个同学喜欢每门课的程度。

（5）对于《演讲与口才》，定义其类型，用(4)提到的方法（即：冯同学喜欢技术类课程的程度5*《演讲与口才》是技术类课程的程度-1+冯同学喜欢语言类课程的程度0*《演讲与口才》是技术类课程的程度4 = -5）。可知，冯同学不喜欢这门课程。

2.2 SVD的数学计算

将高职课程-高职学生的评分矩阵定义为V，且V∈Rn×m,其中，Vij为某位高职学生i 对某门高职课程j 的评分。高职课程不可能获得所有高职学生的评分，因此V 一定是稀疏的。将Course Features Matrix 定义为U，作为高职学生对课程特征的偏好矩阵。将User Features Matrix 定义为M，M 表示高职课程的特征程度课。

图3：隐因子数对K 对实验效果的影响

图4：参数α 对实验效果的影响

图5：参数θ 对实验效果的影响

依据V=UMT，定义损失函数：

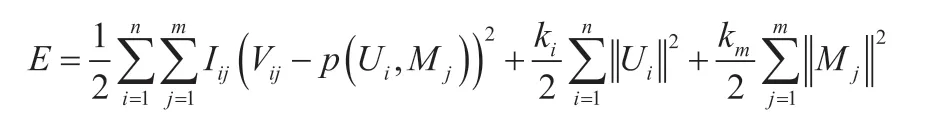
以RMSE 作为评价指标；其中，p(Ui, Mj)代表高职学生i 对高职课程j 的预测，点乘作为预测函数p，p(Ui, Mj)=UiTMj。I∈{0,1}n×m为指示器，高职课程中有评分项的为1，高职课程没有评分项的为0。加上正则化项，防止过拟合。接下来运用梯度下降进行计算，其中u 为学习率。

2.3 SVD的改进

但每个高职学生打分习惯存在差距，比如，林同学与张同学都觉得《python》课程非常好，非常喜欢，但林同学可能只给出3 分，在林同学看来，已经属于非常高的分数，张同学可能会给出5 分。此时，用p(Ui, Mj)=UiTMj对评分进行预测就不太准确了，这里需要对SVD 进行改造。需要依据高职学生的兴趣和课程级别给评分加上偏置，这里qiTpu与UiTMj等价。

其中， 表示全局平均数，bi表示高职学生用户偏置项，bu表示课程偏置项。损失函数变为：

此时，我们的梯度下降也变成了这样：(λ 为学习率) 。bu、bi、pu、qi分别如下：

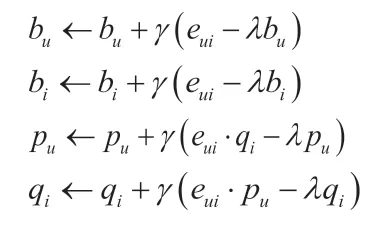
高职在线教学资源在实际应用中，由于评分缺失，显示数据比隐式数据少很多。将高职学生的隐式数据加入模型中，才能形成最终符合高职院校在线教学资源推荐模型。SVD 算法的核心是寻找高职学生、高职课程中隐含的维度，这些隐含数据可能为两两组合，也可能以N 个一起组合。利用SVD 可以学习出高职学生对每个维度的偏好程度。在训练SVD 之前，需要预设维度的数量factors。

3 SVD的代码实现

以python、jupter、numpy、pandas 环境为例,展示SVD 用代码实现计算的过程。

（1）读取数据:import 导入numpy库、pandas库、指定的数据库；

（2）特征值分解；

（3）计算右奇异矩阵。

4 Surprise库训练SVD

通过python3.7 搭建实验平台，选用公开的数据集MovieLens数据集分别对SVD、SVD++、考虑高职学生偏好相似度的算法进行了检验。在评价标准方面选用了RMSE 与MAE，并且进行了比对。其中五分之四为训练集、五分之一位测试集。并且使用了Surprise。其在python 实施中的关键步骤如下:

（1）利用import 导入SVD；

（2）初始化reader,将评分范围设置成1-5 分，并数据格式划分成4 个；

（3）初始化database；

（4）调用 .split.ShuffleSplit()拆分data；

（5）训练模型。

Surprise 训练SVD 的核心代码。

5 实验结果分析

（1）迭代次数=5，λ=0.01，α=0.001，λb=0.05。从5、10 至50，增加隐因子的数量，并观察其RMSE 的变化。隐因子数达到一定数量的时，RMSE 趋于稳定状态。如图3 所示。

（2）λ=0.01λb=0.05，且隐因子数固定k=50。从α=0.01 开始观察并记录RMSE 的变化。在α 值逐渐减少的过程中，其对应的RMSE 值变化趋势是先减少再减少。当α=0.005 时，RMSE 趋于稳定状态。如图4 所示。

（3）α=0.01，λ=0.01，λb=0.05，且隐因子数固定k=50。从θ=0.1 开始观察并记录RMSE 的变化。α=0.65 左右，RMSE 值趋于最小。实验结果如图5 所示。

（4）将所有参数调整到最优的状态下，比较不同算法之间的RMSE 值、MAE 值。如表1 所示。

可得出，融合高职学生兴趣偏好算法RMSE 和MAE 值相比其他两种算法均有所提高，表明本文在考虑高职学生的课程偏好相似度后，将偏好相似矩阵融入 SVD 模型中，提高了评分预测的结果。

6 结语

本文提出基于SVD 构建高职在线教学资源推荐系统，提出了结合高职学生兴趣偏好改进SVD 算法模型。并将设计的算法通过公开电影数据集进行试验与测试。得出改进后的SVD 对RMSE、MAE 有所提高。从信息系统接收模型、用户持续使用意向的文献分析中，可以得知采纳意愿和促成因素正向影响个体对学术社交网站的采纳行为；绩效期望、努力期望正向显著影响用户采纳意愿；学习者的感知有用性与其接受网络课程的行为正相关；MOOC 平台用户知识分享意愿有显著正向影响；感知有用性和内在动机对大学生网络学习空间的使用意向具有显著的直接影响；同时，人们对于知识获取、表现预期、同行/社会压力、娱乐享受的社会心理预期会影响其对网络课堂的使用。推荐系统的研究与实践是跨学科，需要综合考虑诸多因素。旨在构建符合高职学生特征的推荐算法。本次研究探讨了其中一种算法模型的尝试，在用户持续使用行为影响因素等诸多方面，包括高职课程特征、高职学生特征建模方面，存在提取与分类的问题，在下一步研究工作中将对该算法进行改进。

表1：不同算法的RMSE 与MAE 对比表