岩溶管道的折算渗透系数取值探讨

邹昌喜,黄 勇

(河海大学地球科学与工程学院,江苏 南京 211100)

中国作为岩溶最为发育的国家之一,常常需要正确处理岩溶地区的管道流问题[1-2]。岩溶管道流问题的难点在于岩溶管道的强透水性和形态变化的多样性[3-4],主要表现为管道中层流与紊流并存[5],导致常规的达西定律不适用。针对这种情况,有学者从流体力学的水头损失方程出发,提出了岩溶管道的折算渗透系数法,并建立了三重介质模型模拟岩溶管道的水流运动[6]。该方法的合理性和优越性在多次实际应用中得以验证[7],有着广阔的运用前景。但是,此法在折算渗透系数公式的推导中未将局部水头损失纳入总水头损失的范围,而岩溶管道常常形态多变,如出现汇流、分岔、弯折等情况,这种情况下会产生局部水头损失,这种局部水头损失不可忽略[8-10]。尽管对于长直岩溶管道而言这种局部水头损失很小,但有3种情形必须获得考虑局部水头损失的岩溶管道折算渗透系数:(a)岩溶管道较短且出现形态突变的情形;(b)整条岩溶管道弯曲多折或多汇流、分岔等局部水头损失的情形;(c)小尺度岩溶管道流研究中出现水流边界条件发生突变的情形。本文从Izbash指数方程出发,推求考虑局部水头损失的岩溶管道折算渗透系数公式,将其应用于弯折岩溶管道模型的分析计算,并讨论了影响岩溶管道折算渗透系数的主要因素。

1 考虑局部水头损失的岩溶管道折算渗透系数

局部水头损失是水流边界的形状、大小和方向发生急剧变化时引起的水头损失[11],在实际的岩溶管道中,常常由于管道的形态变化引起水流形态改变,产生的水头损失发生在水流边界改变的前后一段局部流程范围之内。管道内流的总水头损失为局部水头损失与沿程水头损失之和[12]:

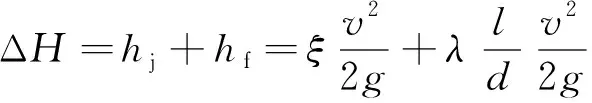
(1)

式中:ΔH——总水头损失;hj、hf——局部、沿程水头损失;ξ、λ——局部、沿程水头损失系数;l——岩溶管道长度;d——岩溶管道直径;v——地下水渗流速度(管道内由于孔隙度为1,渗流速度v等于实际流速u);g——重力加速度。

1.1 Izbash方程中系数α的确定

Izbash指数方程是苏联学者于1931年提出的描述达西流和非达西流运动规律的经验公式,可用于描述岩溶管道流的运动规律[13]:

J=αvm

(2)

式中:J——水力梯度;α——经验系数;m——非达西指数。

m随流态变化而变化,当水流为层流时,m=1;当水流为紊流时,m=2;当水流为层流和紊流的第一过渡区时,m的值介于1～2之间。水力梯度J=ΔH/l,由式(1)(2)可得

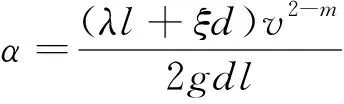
(3)

1.2 折算渗透系数的确定

Izbash方程(式(2))可以改写为

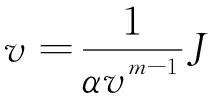
(4)

式(4)与Darcy公式具有相同的形式,将1/(αvm-1)认为是考虑了局部水头损失(hj)和沿程水头损失(hf)的岩溶管道折算渗透系数(KL(f+j)),再代入式(3)得

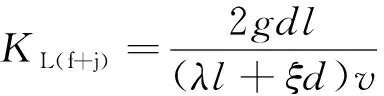
(5)

式(5)中,若ξ=0,即不考虑局部水头损失,则

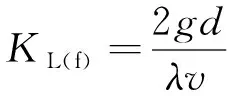
(6)

式(6)与文献[6]中获得的折算渗透系数结果一致,即在研究短岩溶管道和水流边界条件发生强烈改变的区域时,未考虑局部水头损失得出的折算渗透系数会比实际的折算渗透系数偏大。式(5)只考虑了单个位置处的局部水头损失,若考虑多个位置的局部水头损失,则将方程中的ξ替换为多个位置的局部水头损失系数之和∑ξi。实际应用中应根据具体的水流边界条件选用合适的局部水头损失系数值,而λ的取值可参考文献[6,14]的研究成果。

2 弯折岩溶管道模型的折算渗透系数计算

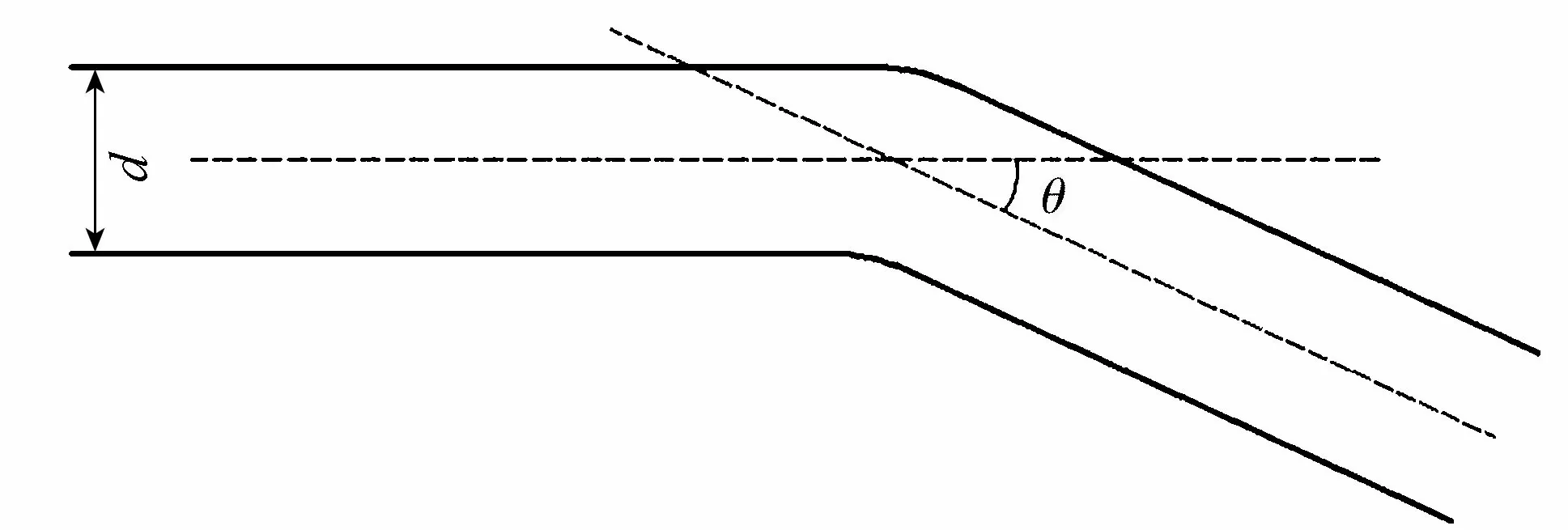
图1 弯折岩溶管道概念模型Fig.1 Conceptual model of the bent karst conduit

为验证上文推导的折算渗透系数公式的合理性,设计了一个长度较短的弯折岩溶管道模型(图1),该模型将实际弯转的岩溶管道进行了概化。图1中管道总长度l=10 m、d=0.5 m,粗糙度Δ=0.001 m,水流的运动黏滞性系数νw=1.306×10-6m2/s,岩溶管道的弯折角度为θ。假定在转弯处产生了局部水头损失,分别计算未考虑局部水头损失和考虑局部水头损失情况下的折算渗透系数。

由式(5)(6)可知,要获得折算渗透系数,需要确定管道内的水流速度。将雷诺系数Re设定为1×103、1×104、1×105和1×106,根据Re和相对光滑度d/Δ可确定管道流分别处于层流区、水力光滑区、第二过渡区和水力粗糙区[11]。管道内的水流速度:

(7)

λ、ξ的取值可参考文献[6,11,14]获得,即

(8)

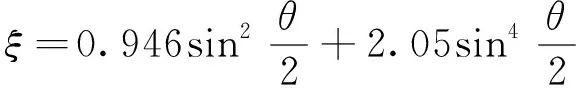
(9)

将式(7)～(9)分别代入式(5)(6)得

(10)

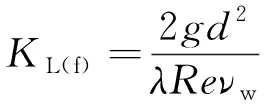
(11)

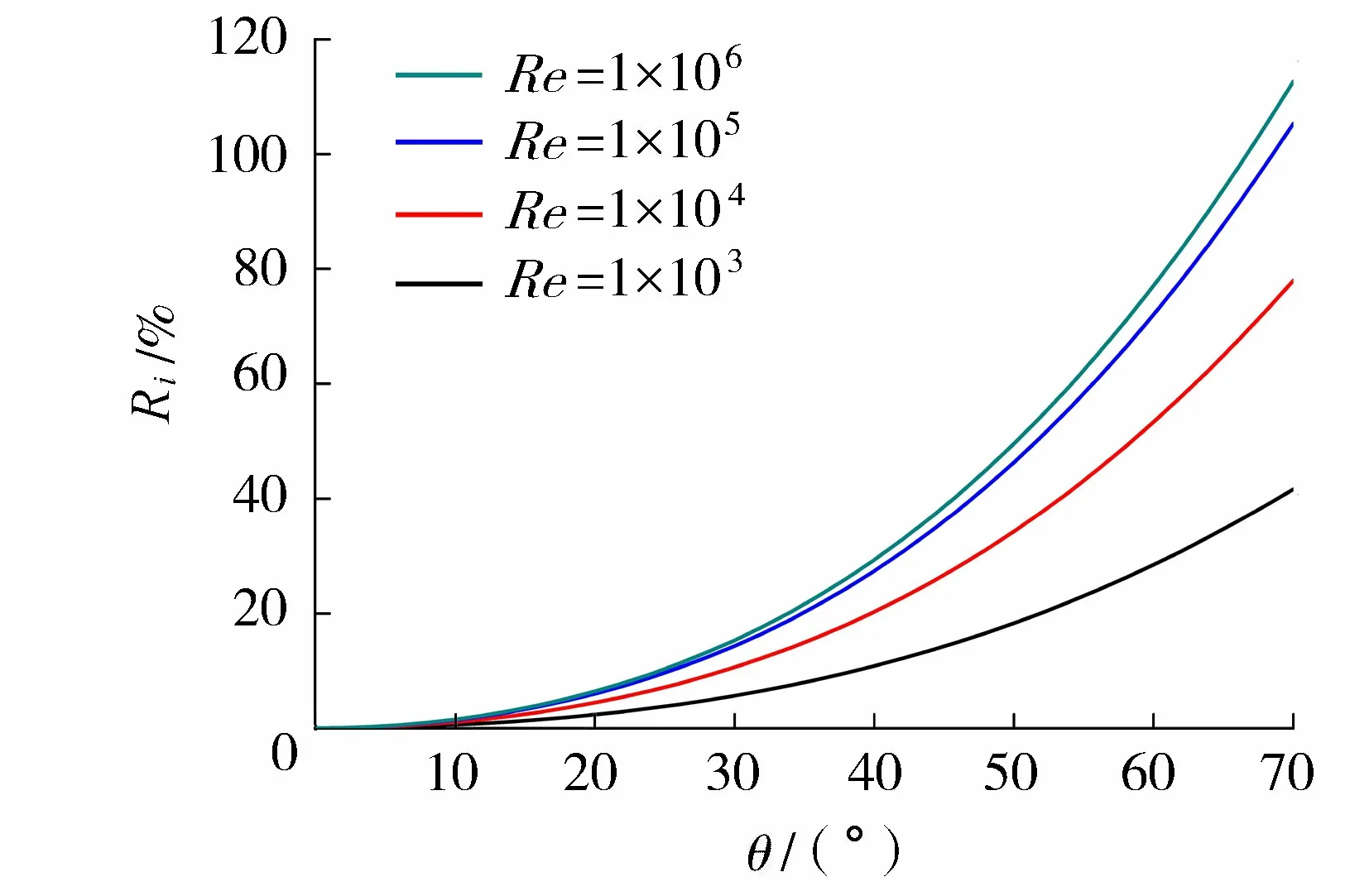
图2 各雷诺系数下增幅随弯折角度变化关系Fig.2 Relationship between Ri and θ under different Re condition

由式(10)(11)可知折算渗透系数与弯折角度的关系:(a)当Re一定时,随着θ增加,KL(f+j)逐渐减小;KL(f)不变,比KL(f+j)偏大。(b)采用增幅函数Ri=(KL(f)-KL(f+j))/KL(f+j)×100%反映KL(f)比KL(f+j)增大的幅度。由图2可知,同一Re下,θ越大,局部水头损失和Ri越大;θ一定时,Re越大,Ri越大。

综上可知,在岩溶管道较短的条件下,管道流的大雷诺系数和水流边界条件的急剧变化会产生较大的局部水头损失,计算折算渗透系数时应考虑到这种情况,因此式(5)计算的岩溶管道折算渗透系数较符合实际情况。

3 折算渗透系数的敏感性分析

敏感性也称敏感度,它能反映模型参数的改变对地下水流模拟计算结果的影响程度[15-16],若模型计算结果对某个参数的细小改变响应明显,则说明该参数敏感性大,此模型受该参数的影响大。本文模型参数主要有4个:Re、d、l和θ。

目前常用的敏感性分析方法有单因素分析法和正交试验法[17-18]。本文采用单因素分析法进行敏感性分析。4个流态分区中均选取Ri为10%时模型各参数的值为初始值(表1),用于计算初始折算渗透系数。分别对各参数初始值作上下10%和20%的变化水平,计算此4种水平下折算渗透系数的大小。采用敏感性指数L作为判断参数敏感性大小的指标[19],即

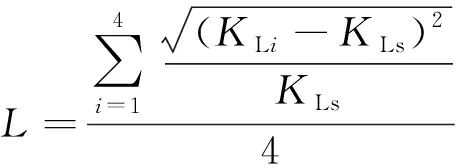
(12)

式中:KLi——各水平参数变化下计算的折算渗透系数;KLs——初始折算渗透系数。式(12)表明,L值越大,岩溶管道折算渗透系数对此参数的响应越明显,敏感指数L计算结果如图3所示。

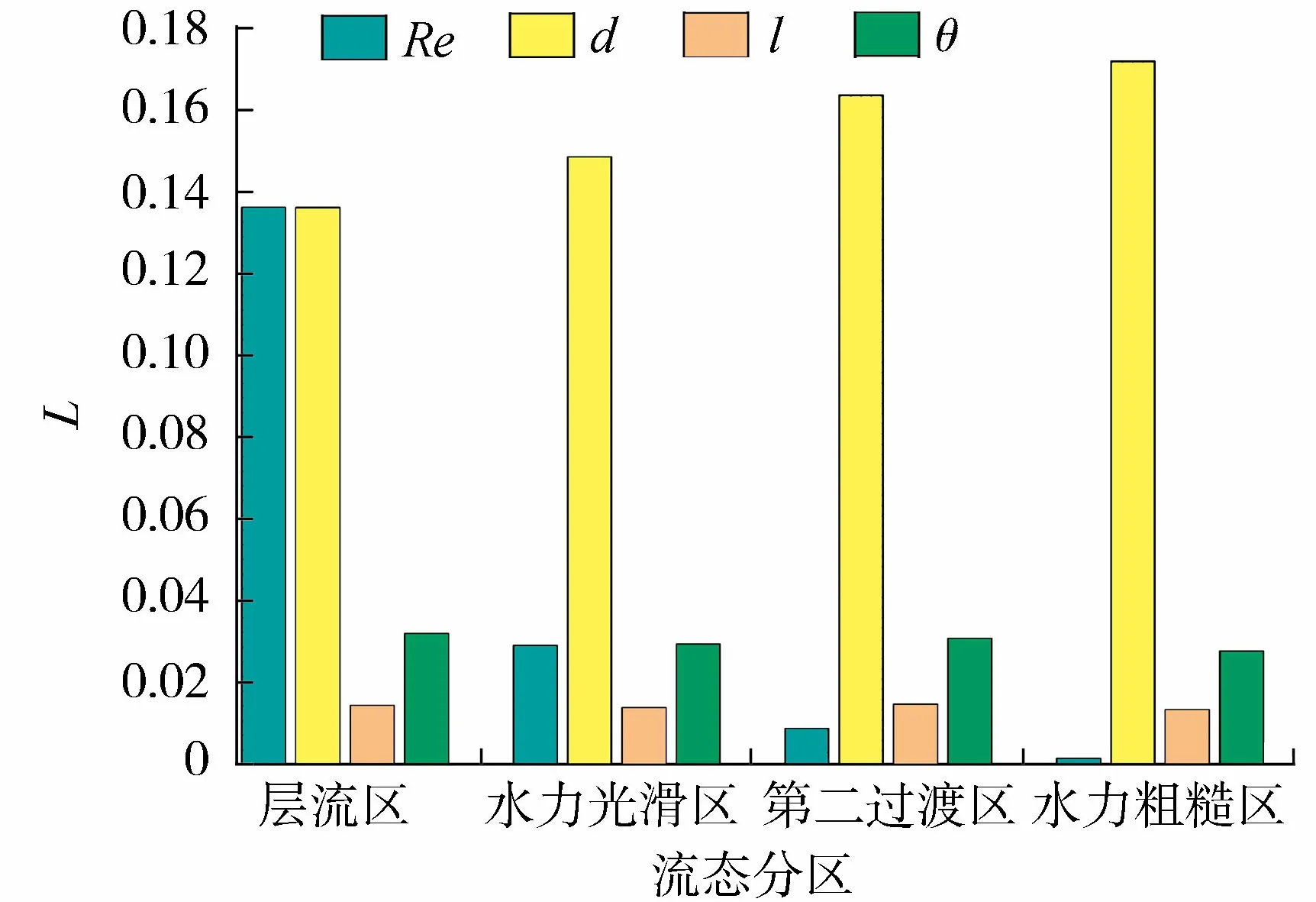
图3 各参数的敏感性分析结果Fig.3 Sensitivity analysis results of each parameter

表1 各参数初始值

Table 1 Initial value of each parameter

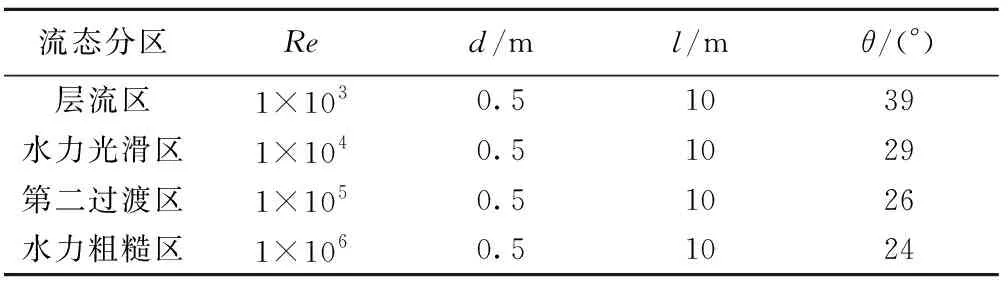
流态分区Red/ml/mθ/(°) 层流区1×1030.51039 水力光滑区1×1040.51029 第二过渡区1×1050.51026 水力粗糙区1×1060.51024

敏感性分析结果表明,影响折算渗透系数最大的参数是d,不论管道水流处于何种流态,d的敏感性指数最大。在层流区,模型的折算渗透系数对雷诺系数的响应程度很大,与d相当,θ和l的敏感性指数次之;在其他3个流态分区内,θ的影响起着次要的影响作用,Re和l影响相对较小。

4 结 论

a. 在长度较短的岩溶管道出现水流边界条件突变,产生的局部水头损失较大的情况下,计算岩溶管道的折算渗透系数要考虑局部水头损失。

b. 在弯折岩溶管道模型中,弯折角度越大,产生的局部水头损失越大,未考虑局部水头损失的折算渗透系数偏大。

c. 本文弯折岩溶管道模型中,影响折算渗透系数最大的参数是岩溶管道的直径,雷诺系数只在层流区影响较大,其他3个流态区雷诺系数、弯折角度和岩溶管道计算长度影响与管道直径相比较小。