基于机器学习的蒸散量插补方法

刘 堃，何祺胜，荆琛琳，李金阳，陈 丽

(河海大学地球科学与工程学院,江苏 南京 211100)

蒸散量(ET)作为地表能量平衡和水文循环的重要组成部分[1]，决定着地表生态系统的水热传输，其准确的测定和估算，对于区域水资源评定、水分利用效率、干旱预测等均具有十分重要的价值。经过20多年的发展，涡动相关仪已经广泛应用于地表和大气的能量交换观测[2-3]。涡动相关仪的观测数据通常是以30 min为一个周期，采集1 d和1 a的通量数据[4]。然而，在观测过程中，由于各种原因(降雨、仪器故障、人为误操作等)部分观测数据会缺失，研究表明一年中有17%～50%的观测数据会缺失和被剔除[5]。因此，如何建立有效的数据插补方法来形成完整的通量数据集成为当前亟待解决的问题[4]。国内外学者针对涡动相关仪缺失的蒸散量提出了多种数据插补方法[6]，主要有非线性回归、动态线性回归、查找表、昼夜平均、卡尔曼滤波、人工神经网络(ANN)方法等。

目前，机器学习算法已经广泛应用于遥感研究。对于蒸散量的插补，国内外学者主要采用ANN方法进行插补[7-9]，并取得了较好的精度。但是使用其他机器学习算法(例如决策树、随机森林等)进行插补的研究却鲜有报道。此外，土壤湿度作为蒸散发的重要因子，对许多生态系统的蒸散发都有不同程度的影响[10]，而有关土壤水分要素的参与对基于机器学习的蒸散量插补结果的影响研究很少。

本文以典型干旱半干旱区湿地、农田、草地、林地生态系统为研究对象，研究作为输入变量的气象因子与蒸散量观测值之间的相关性，分析多元线性回归(MLR)、决策树(CART)、随机森林(RF)、支持向量回归(SVR)、BP人工神经网络(BPANN)、深度学习算法(DL)对缺失蒸散量的插补效果，以及土壤水分的参与对机器学习算法插补精度的影响，以期能为不同生态系统涡动相关仪观测蒸散量的插补提供理论支持。

1 数据和方法

1.1 数据选择

黑河流域位于中国西北干旱半干旱地区(97.1°E～102.1°E，37.7°N～42.7°N)，是中国第二大内陆河流域，属于典型的温带大陆性干旱气候，气候干燥，降水稀少。黑河流域上游祁连山是高寒半干旱区，中、下游分别为河西走廊和额济纳平原干旱区，东西和南北差异特征显著，生态环境比较脆弱。本文主要研究黑河流域湿地、草地、农田、林地(柽柳、胡杨林、混合林)等生态系统。研究所用数据主要来自6个站点(表1)，这6个站点均建有自动气象站和涡动相关仪，具有蒸散量、显热通量、气象因子等的长期连续观测数据(来源于黑河生态水文遥感试验(HiWATER)[11-12]，可以从寒区旱区科学数据中心申请获得(http://westdc.westgis.ac.cn))。每个站点涡动相关仪输出的都是30 min蒸散量均值，自动气象站输出的为10 min气象因子均值；由于仪器损坏、质量控制等原因，实际蒸散量输出值都有不同程度的缺失，数据缺失状况见表1。

表1 站点基本信息

采用每个站点30 min的有效气象因子和蒸散量观测值研究机器学习算法的插补效果，将气象因子作为输入变量，蒸散量观测值作为响应变量。草地、农田、林地生态系统用的气象因子为净辐射、温度、土壤热通量、相对湿度、风速、土壤体积含水率(表层2 cm深度)。对于湿地生态系统，因为缺少实测土壤体积含水量，同时考虑到湿地常年积水，土壤体积含水量对蒸散发的影响低于其他气象因子[13]，因此选用净辐射、温度、土壤热通量、相对湿度和风速作为气象因子。

1.2 数据预处理

由于输入变量各不相同，也不在同一个数量级上，为了消除各变量数量级差异对插补结果的影响，同时也为了加快人工神经网络和深度学习的训练和收敛速度，需要对输入变量做归一化处理。归一化公式如下：

(1)

式中：Y—— 输入变量归一化值；x—— 输入变量；xmin、xmax—— 输入变量的最小值和最大值。

1.3 6种机器学习算法

本文采用的机器学习算法包括MLR、CART、RF、SVR、BPANN、DL。

a. 多元线性回归。该算法是指2个或2个以上的自变量组成线性表达式对应一个因变量，通常用在自变量和因变量具有线性相关的条件下。

b. 决策树。决策树是以平方误差最小化准则来不断地分裂节点，从而递归地构建二叉决策树，并最终以叶子节点的均值作为预测值。经反复试错，该算法的参数中，树的最大深度和节点样本数分别设置为20和11，其他参数保持缺省值不变。

c. 随机森林。随机森林通过集成学习的思想将多棵决策树集成[14-15]，再通过取所有树预测均值得到RF的预测值 。其不易发生过拟合，并具有很好的鲁棒性。经反复试验，该算法参数中，决策树个数、每颗树的最大深度和节点样本数分别设置为100、30和1，其他参数保持缺省值不变。

d. 支持向量回归。支持向量回归是一种建立在统计学习理论的机器学习方法，通过结构风险最小原理取得全局的最优解[16-18]。SVR速度快，泛化能力强，能够解决小样本和高维输入空间的问题。经测试，SVR选用RBF作为核函数，惩罚系数C设置为200，核函数参数G设置为25。

e. BP人工神经网络。BP人工神经网络是一种学习过程为信号正向传播和误差反向传播的前馈神经网络，是目前应用最广泛的一种神经网络[19]。目前，国内外主要采用3层神经网络结构来插补蒸散量[7,9]，且从理论上说，单隐层BP网络已经有足够的映射或逼近能力。因此，本文采用3层网络结构，分别由输入层、隐藏层和输出层组成。每层的激活函数均设为relu函数,经实际测试，把隐藏层单元个数设为200，此时插补结果最佳。

f. 深度学习。深度学习是在传统人工神经网络的基础上添加更多的隐藏层，以此建立复杂的非线性网络结构，从而在少量有限的样本中挖掘出数据的本质特征，用较少的参数建立复杂的函数。本文采用增加BP人工神经网络隐藏层数量的深度学习算法，把隐藏层设为4层，每层70个神经元，每层的激活函数设为relu函数，并且为了防止过拟合，把参数L2(正则化项)的值设为0.01。

上述算法中，除了深度学习是基于Python语言的keras模块建立的模型，其他算法均是基于Python语言的skicit-learn模块建立的模型。

1.4 插补模型的建立与性能评价

综合考虑数据质量和气象数据的缺失程度，分别选取草地(2016年全年)，农田、林地(均为2015年全年),湿地(2015-01-01至2015-09-25)生态系统中的10 min气象数据和30 min蒸散量观测值作为研究数据。因为气象数据缺失很少，因此采用线性插值法补充完整[20]，同时为了与30 min蒸散量相对应，把10 min气象数据取均值处理为30 min气象数据。选用各生态系统30 min蒸散量未缺失部分和对应的30 min气象数据作为训练和测试样本数据的来源，其中训练样本用于插补模型的训练，测试样本作为人工制造的缺失值，通过训练好的模型在测试样本上的模拟值与测试样本的观测值(真值)进行比较，研究插补的效果。选用决定系数R2、均方根误差RMSE、绝对平均误差MAE评价测试样本模拟值与观测值之间的相关性与离散程度。

2 结果与分析

2.1 蒸散量与气象因子的相关性分析

为了确定所选气象因子对于蒸散量插补的有效性，选取湿地、草地、农田、林地的输入气象因子与对应的蒸散量观测值进行相关性分析。结果(表2)表明，在置信度水平为0.05和0.01时，湿地、草地、农田、林地的蒸散量均与所选气象因子存在显著相关关系。因此，可以选用净辐射、温度、土壤热通量、相对湿度、风速、土壤体积含水率6个气象因子来建立插补模型。

2.2 蒸散量模型插补结果

采用不同机器学习算法计算湿地、草地、农田、林地在有无土壤体积含水率情况下蒸散量的插补值，其与观测值之间的R2、RMSE和MAE见表3。

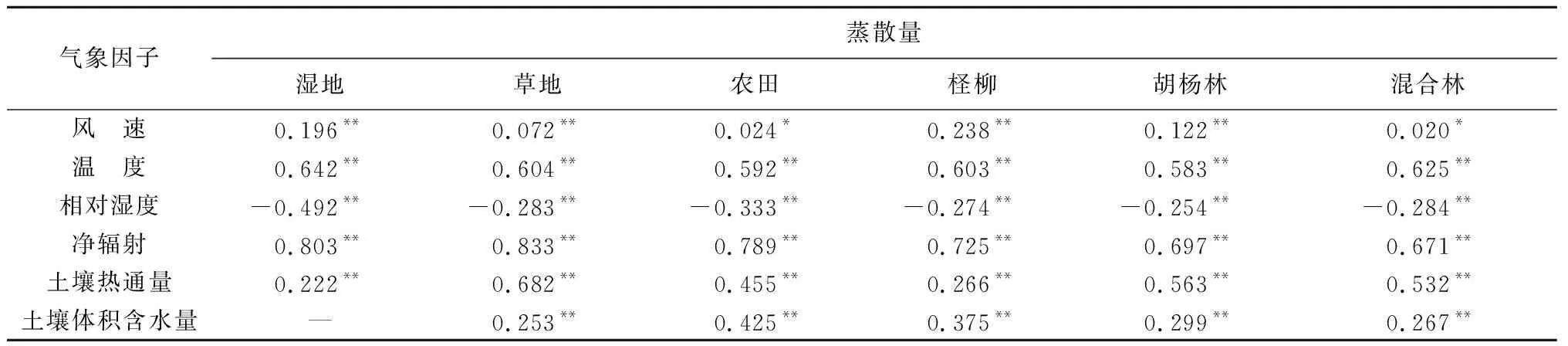
表2 蒸散量与气象因子间的相关性

注：*是在0.05水平上双侧显著相关；**是在0.01水平上双侧显著相关。

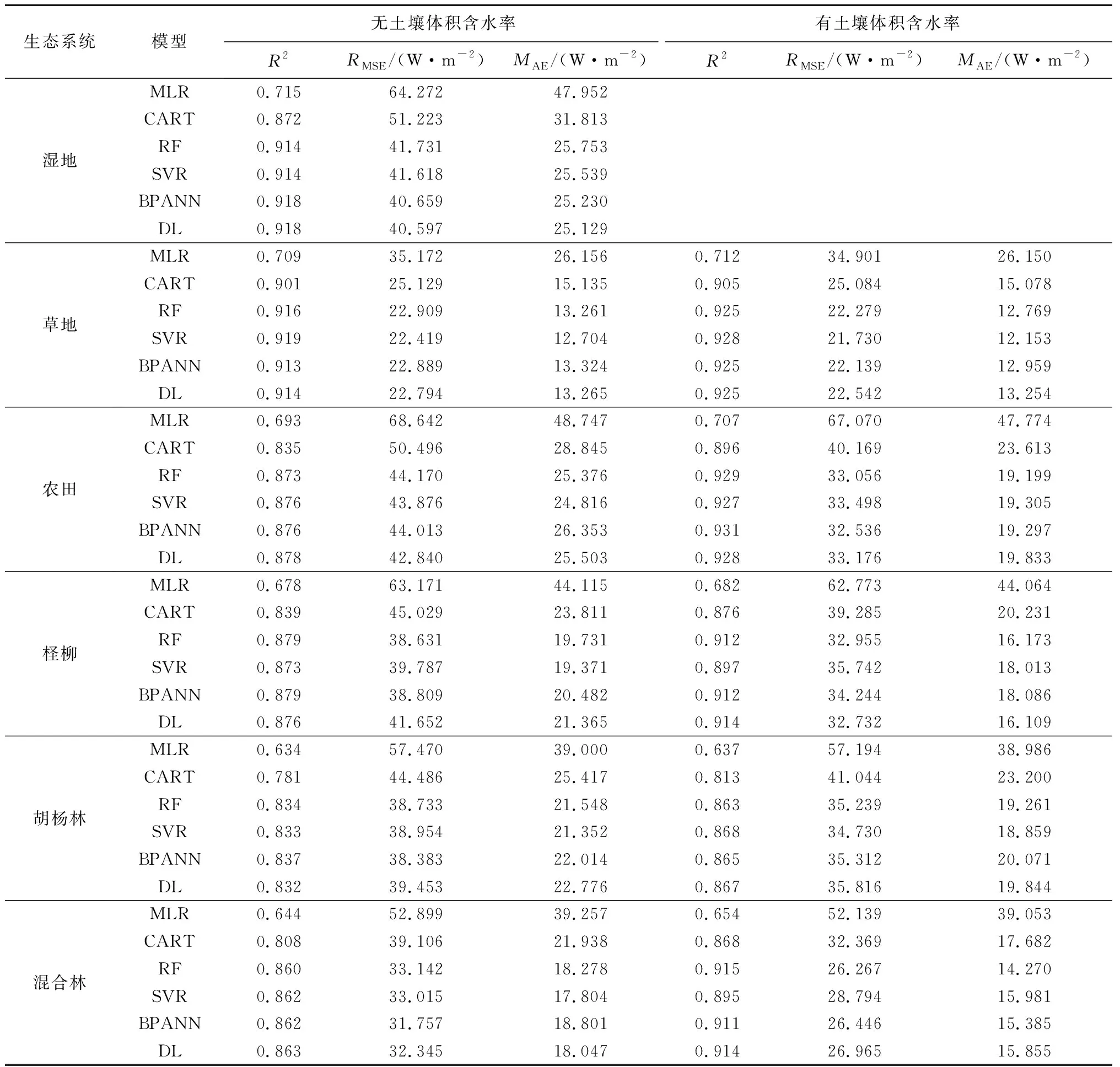
表3 6种机器学习模型蒸散量的插补结果

注：有无土壤体积含水率指输入变量是否含有相应的值。

整体来看，各生态系统最好插补结果的决定系数都比较高(R2>0.83)，其中草地和农田模拟结果最好，其次是湿地、柽柳和混合林，胡杨林模拟结果最差。

由表3可知，MLR在每种生态系统的插补均表现最差，这表明气象因子与蒸散量之间是复杂的非线性关系，不适合用简单的线性模型。其次，CART要好于线性回归的插补结果，而相比MLR、CART，RF、SVR、BPANN、DL在每种生态系统的结果均更好。在湿地、草地、农田、胡杨林生态系统中，RF、SVR 、BPANN、DL算法的结果差异并不是很显著。柽柳、混合林生态系统，SVR的结果要稍差于RF、BPANN、DL的结果，可能是因为柽柳、混合林的实测气象数据和蒸散量包含一些噪声，而SVR对数据噪声比较敏感[21]，导致噪声带来的错误被扩大，从而影响了插补结果。总之，对于干旱半干旱区的湿地、草地、农田、林地生态系统，RF、BPANN、DL、SVR均可以得到较理想的插补结果，但是SVR稳定性稍差于其他3种方法。

相比无土壤体积含水率情况，在土壤体积含水率参与的情况下，农田、柽柳、胡杨林、混合林的R2、RMSE、MAE均有显著提高，但草地相比却并没有显著提高。在蒸发旺盛的生长季(3—10月)，草地的土壤体积含水率大部分都在30%以上(图1)，相比其他生态系统，其下垫面水分比较充足，这导致土壤水分对蒸散发的影响相对较弱；同时草地生态系统中土壤水分与蒸散发的相关性最弱(表2)，这些因素表明，在半小时尺度下草地生态系统的土壤水分对蒸散发的影响程度相对较弱。因此，土壤水分的加入并未使草地的插补精度有明显提高。

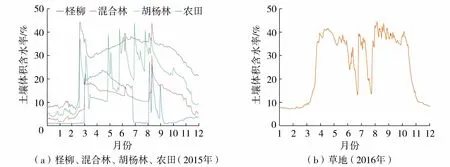
图1 林地、农田、草地的日土壤体积含水率变化Fig.1 Change of daily soil moisture in farmland, woodland and grassland

为了研究插补模型的泛化能力，选用草地(2015年)、农田(2016年)、柽柳(2016年)、胡杨林(2014年)、湿地(2016年)生态系统的气象数据和蒸散量观测值(气象因子和时间尺度与训练模型保持一致)作为测试样本，用已训练好的插补模型计算测试样本的模拟值，并与测试样本的真值进行比较。从整体结果看，无论土壤水分是否参与，各生态系统在其他年份的插补精度均有一定程度的降低。其中草地插补精度降低的幅度最小(R2降低0.02～0.03)，最好模拟精度为R2=0.9～0.91，RMSE=31.817～32.446 W/m2，MAE=17.232～18.627 W/m2，而湿地、农田、柽柳、胡杨林、混合林插补精度降低的幅度较大(R2降低0.1～0.2)。

2.3 插补效果分析

为了检验机器学习算法对蒸散量的插补效果，以农田为例，采用人工神经网络算法，分别选用有土壤体积含水率和无土壤体积含水率2种数据集，对2015年缺失蒸散量进行插补，得到一年连续的蒸散量，并以6月8日为例分析插补效果(图2中虚线框代表原始观测值缺失部分)，同时将插补完整的蒸散量与净辐射进行比较和分析，结果见图2～3。

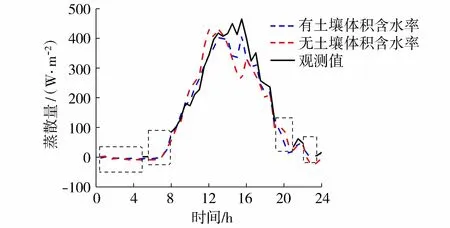
图2 蒸散量插补效果Fig.2 Gap-filling effect of latent heat flux

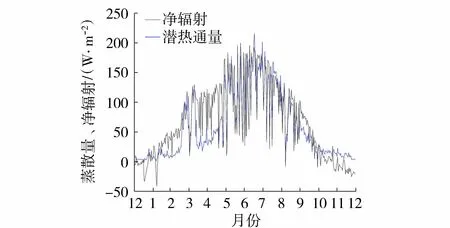
图3 插补完整蒸散量与净辐射日变化对比Fig.3 Comparison of interpolation completed latent heat flux to net radiation

由图2可以看到有土壤水分参与的结果要优于无土壤水分参与的结果，更贴近实测曲线的变化趋势。净辐射作为蒸散发的能量来源，是影响蒸散量变化的主要因子，从蒸散量与净辐射的变化趋势可对插补效果做定性分析。从图3可以看到，两者变化趋势比较接近，有较好的相关关系。通过上述分析，表明插补结果比较合理可信。

3 结 语

MLR在各个生态系统的蒸散量插补精度均最差(R2=0.6～0.7)，CART次之(R2=0.78～0.9)，而RF、SVR、BPANN、DL的插补精度较高(R2=0.83～0.93)；在柽柳、混合林生态系统，相比RF、BPANN、DL，SVR的插补精度稍低，表明其稳定性偏差。此外，土壤水分参与插补要比土壤水分不参与插补可以获得更高的精度(R2提高了0.01～0.06)。以已建立的插补模型去插补其他年份的蒸散量，发现其精度有不同程度的下降。

综合考虑模型的插补精度和稳定性, 对干旱半干旱区湿地、草地、农田、林地生态系统,随机森林(RF)、BP人工神经网络(BPANN)、深度学习(DL)更适合用来插补，可以取得较好的结果，同时加入土壤水分可以在一定程度上提升机器学习模型插补的精度。

本研究虽较全面地分析了MLR、CART、RF、SVR、BPANN、DL对干旱半干旱区生态系统缺失蒸散量的插补效果、但这些算法在湿润区、干旱区等其他环境的生态系统是否适用，还需要进一步的研究和验证。