河道洪水演算方法在淮河及滹沱河中游的应用

李致家,何 蒙,闫凤翔,胡友兵,刘志雨,童冰星

(1.河海大学水文水资源学院,江苏 南京 210098; 2.河北省水文水资源勘测局,河北 石家庄 050031;3.淮河水利委员会水文局,安徽 蚌埠 233000; 4.水利部水文局,北京 100053)

根据河段上断面入流过程,应用洪水波运动的数学描述方法解出流量的时空变化函数或者某一指定下断面的流量过程,称为河道洪水演算[1]。常用的演算方法有2 种：基于水量平衡与槽蓄方程的水文学方法和基于圣维南方程组及其简化算法的水力学方法[2]。水文学方法计算相对简单、资料需求相对较低，易于在实时洪水预报中应用,在我国洪水预报中应用广泛,其中最为典型的方法是马斯京根法[1,3-4]。马斯京根法假定出流与槽蓄量成线性函数关系,同时流量在计算时段内和沿程变化呈直线分布,参数要利用实测洪水资料率定,或者根据参数的水力学公式估算[3]。我国河流众多,水流条件复杂多变,同时受人类活动影响,河道的断面形状和水力特性可能发生变化，因此，本文选用Muskingum-Cunge-Todini(MCT)可变参数法和非线性水库法进行河道洪水演算。选用的2种演算方法能够考虑河道断面形状和水力特性,在国外已经取得较为广泛的应用[5-6]。选取湿润地区淮河中游吴家渡—小柳巷河段及半干旱地区滹沱河中游黄壁庄—北中山河段为典型单一河段验证这2种演算方法在不同在流域的适用性,并将模拟结果与马斯京根法进行分析比较。

1 方 法 原 理

1.1 马斯京根法

19世纪70年代圣维南建立明渠非恒定流偏微分方程组，为洪水研究奠定了理论基础[7]。McCarthy于1938年提出马斯京根法，开创了洪水演算的水文学方法[8]，其流量演算方程式为

O2=C0I2+C1I1+C2O1

(1)

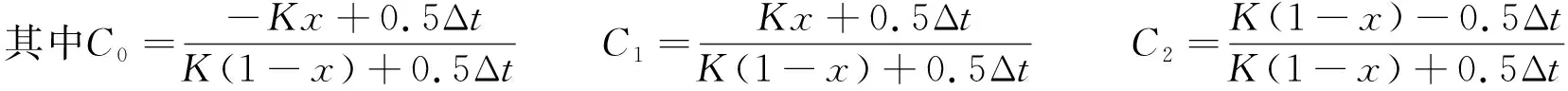
式中：O1、O2——计算时段始、末的河段出流量；I1、I2——计算时段始、末的河段入流量；C0、C1、C2——流量演算系数；K——蓄量常数；x——流量比重系数，与洪水波的坦化变形程度有关；Δt——计算时段长。

马斯京根法采用线性有限差解，要求水面线为直线且流量沿程线性变化，因此演算时段Δt应等于或接近K值[9]。但在长河段的情况下，K远大于Δt，这时需要采用分段马斯京根法[10]。

1.2 MCT可变参数法

1969年Cunge在Muskingum法的基础上提出M-C方法，开辟了应用运动波数值扩散进行洪水演算的新途径[11]。1978年Pouce和Yevjevich在Cunge的基础上，考虑到波速的变动问题，建议采用变动参数表示动力波速和水面宽度，提出了变动参数M-C方法[12]。但在变动参数M-C方法的实际应用中，发现了2个问题：一是质量不守恒问题[13]；二是蓄量不稳定问题[14]。由此，Todini对变动参数M-C方法进行修正，提出一种新的质量守恒和稳定状态协调的Muskingum-Cunge-Todini可变参数法(简称为MCT可变参数法)(式(2))，并用于TOPKAPI模型中[14-17]。

Ot+Δt=C1It+Δt+C2It+C3Ot

(2)

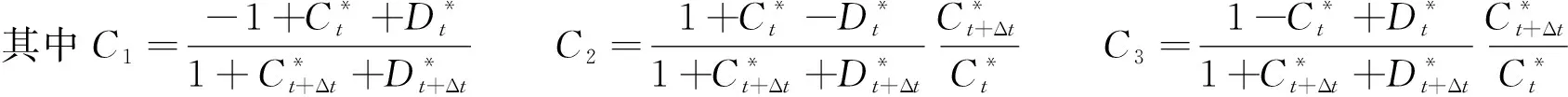
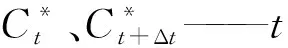
1.3 非线性水库法

运动学方法中采用曼宁公式近似动量方程，得到非线性水库方程的一般形式：

(3)

式中：y——河道蓄水量；a、b、c——系数，在每个时间步长内为不变量。

刘志雨等[18-19]、Todini等[20]发现对式(3)中的指数项进行二次方程近似，可将复杂的指数方程转化为低阶方程并得到解析解。假设河道为树形结构，河段为三角形断面，非线性水库方程的具体表达式为

(4)

式中：Vc——河道蓄水量；rc——旁侧入流量，包括地表径流量和到达河道的土壤排水量；Qc——来自河道上游的入流量；S0——河底比降，假定与地形坡度相同；n——河道曼宁糙率系数；γ——河道侧边与水平线的夹角；Δx——计算步长。

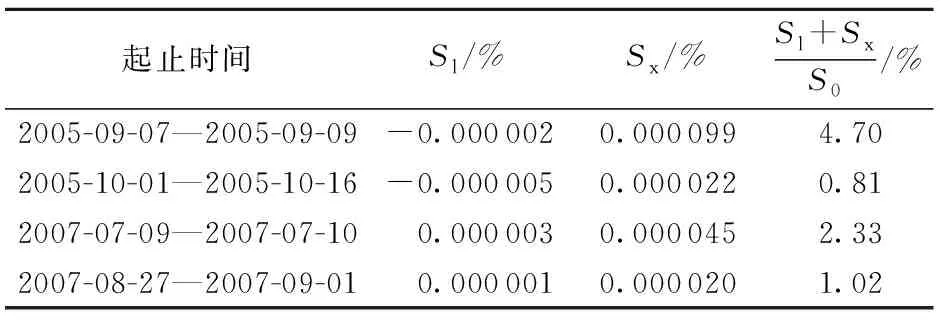
表2 2005年、2007年吴家渡—小柳巷河段惯性项

注:Sl为局地惯性项,Sx为迁移惯性项。

2 淮 河 算 例

2.1 河道概况

淮河干流中游吴家渡—小柳巷河段长约94 km,河床糙率约为0.02～0.025[21]。从吴家渡到小柳巷依次分布有方邱湖行洪区、临北缕堤湖行洪区、花园湖行洪区、香浮段行洪区、潘村段行洪区[22]。除花园湖行洪区偶尔使用之外,受上游诸多闸门调度与行蓄洪区拦蓄作用影响,其他行洪区很少有机会使用。由于北淝河上的沫河口闸、怀洪新河上的五河闸常年关闭,这2条河的来水少有机会汇入干流,因此吴家渡—小柳巷河段干流受支流来水影响较小,本文不予考虑。另外由于小柳巷以下河道较为顺直,且离洪泽湖较远,因此受洪水顶托作用较小。

吴家渡到小柳巷纵剖面变化剧烈,最浅处与最深处深泓高程相差较大[22]。纵剖面的急剧变化导致水流更加紊乱,河道形状阻力加大。根据吴家渡、临淮关、五河、小柳巷4个站的实测断面资料,计算出平均河底比降约为0.002 06%,并将河道断面形状概化为河床夹角沿程变化的三角形,体现河段上下游的断面形状变化。

2.2 洪水波水力特征分析

2.2.1 附加比降分析

直接测定附加比降十分困难,所以一般认为附加比降SΔ近似等于水面比降S与河底比降S0之差[3]。选取2003年、2005年、2007年作为典型年,根据实测的吴家渡、临淮关、五河、小柳巷的日均水位资料, 选择吴家渡、小柳巷两站水势平稳及流量接近的日期计算吴家渡—小柳巷河段水面比降S,并推求出洪水波的附加比降,结果见表1。

表1 2003年、2005年、2007年吴家渡—小柳巷河段水面比降和附加比降

注:各河段的河底比降S0均为0.002 06%,SΔ为负值是因为计算日期处于落洪期。

一般约定波前即涨洪段的附加比降为正,波后即落洪段的附加比降为负。2003-09-27、2005-10-09临淮关—五河段的附加比降为正值,是因为2003年、2005年洪水较大,临淮关—五河段的水面比降大于吴家渡—临淮关段和五河—小柳巷段,是阻水河段,使得洪水波的附加比降出现正值。可以看出:落洪期附加比降占河底比降为4%～10%,且涨洪期附加比降一般大于落洪期附加比降的绝对值,占比将更大,其影响不可忽视。

2.2.2 惯性项分析

由于2003年没有实测流速资料,仅对吴家渡—小柳巷河段2005年、2007年计算时段内的惯性项进行分析,结果见表2。本河段洪水波惯性项仅占河底比降1%～4%,故可以忽略。

由表1～2可知,动力方程中惯性项占河底比降的比例相当小,可以忽略;而附加比降项占河底比降的比例较大,不能忽略。因此吴家渡—小柳巷河段扩散波特征明显。

2.3 河道洪水演算方法的参数率定

选取2003—2017年大、中、小洪水共15场进行洪水流量过程模拟,前9场用于参数率定,其余6场用于检验模型。为减少土壤、地表和河道等蓄水初始条件对计算精度的影响,将洪水发生的前一个月作为预热期,以吴家渡实测流量作为输入进行河道洪水演算。通过人工试错,结合流域实际情况,将3种演算方法的时间步长定为1 h,河段分为16段,确定河床糙率为0.022,分段马斯京根法x=-0.3。

2.4 河道洪水演算结果

由表3可知:(a)非线性水库法和分段马斯京根法的洪量相对误差都在±10%以内,MCT可变参数法洪量相对误差只有1场超过-10%,其余场次结果均较好。(b)非线性水库法和分段马斯京根法洪峰相对误差都有2场超过±20%,而MCT可变参数法的洪峰相对误差都在±20%以内,精度高于其他2种方法。(c)3种演算方法的峰现时间误差在各场次洪水间变化较大,但是平均误差都在±5 h以内。总体上来看MCT可变参数法的峰现时间误差除在20050707、20160616、20170923场次洪水模拟中较大,其余场次模拟结果较好。(d)非线性水库法和MCT可变参数法的确定性系数有2场小于0.9,分段马斯京根法的确定性系数有1场小于0.9。

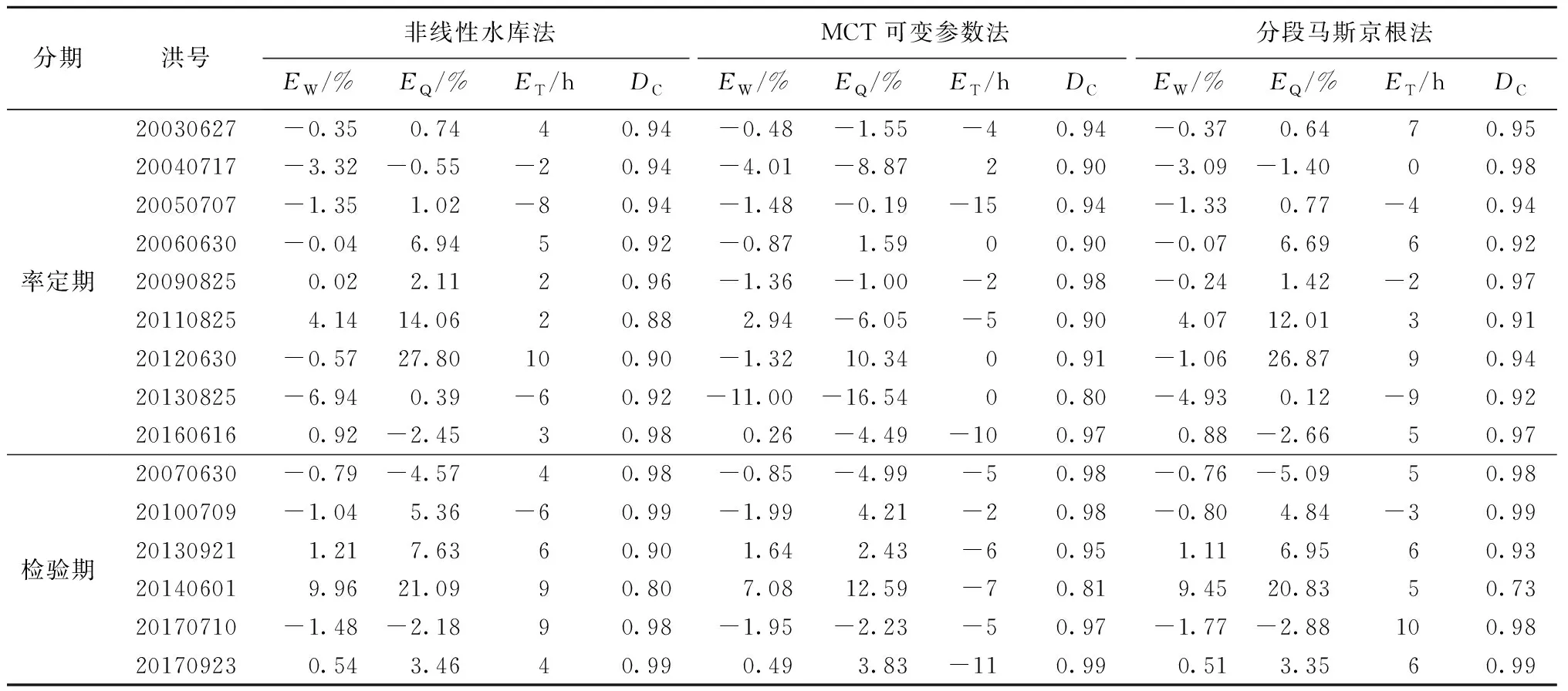
表3 淮河3种河道洪水演算方法模拟结果

注:EW为洪量相对误差,EQ为洪峰相对误差,ET为峰现时间误差,DC为确定性系数。

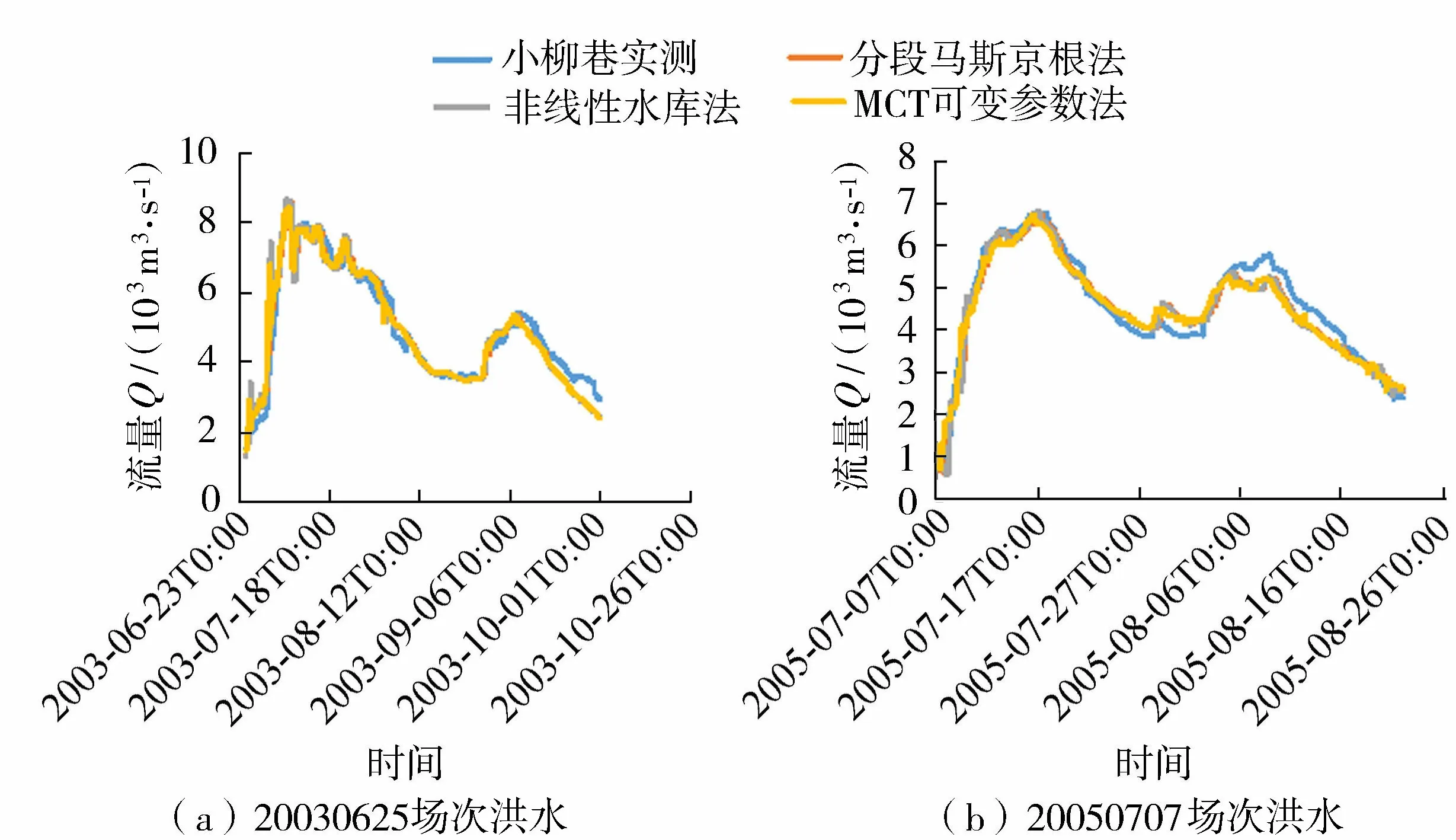
图1 小柳巷洪水模拟结果Fig.1 Flood simulation results in Xiaoliuxiang

综合表3和图1分析,可得:MCT可变参数法对20130825场次洪水模拟结果较差,洪量相对误差为-11%,洪峰相对误差为-16.54%。是因为本场洪水量级明显小于率定期其他场次洪水,区间入流影响较大且洪水历时偏短,洪水陡涨陡落。由于伪数值扩散的存在,MCT可变参数法在小洪水模拟过程中扩散效果偏大,导致洪峰流量偏小,洪量偏小。而基于水量平衡方程的非线性水库法和分段马斯京根法模拟效果较好。个别场次洪水MCT可变参数法的峰现时间模拟结果较差的原因是:(a)本次参数是人工率定结果,率定过程中侧重于确定性系数和洪峰相对误差,不能全面考虑洪水过程的特征指标。(b)河道断面概化较简单,没有考虑滩地的行洪过程。(c)河床糙率对峰现时间的影响。参数率定中河床糙率对洪峰流量、峰现时间都有影响,改变峰现时间的同时可能会影响模拟洪峰值,使得峰现时间的模拟结果不理想。(d)淮河中游河段倒比降的影响。根据实测资料及相关研究[23-24],淮河中游以浮山为转折点,吴家渡—浮山段平均深泓沿程降低,呈正比降;浮山—小柳巷段平均深泓沿程增大,呈负比降,致使淮河中游洪水无法通畅下泄,模拟结果与实际情况相差较大。

总体上看3种演算方法在研究河段上都取得了较好的模拟效果,且MCT可变参数法和非线性水库法在研究河道上模拟精度较高,洪峰合格率均在86%以上,确定性系数均大于0.8,表明这2种方法可以为河道洪水演算提供新的解决方案。

3 滹沱河算例

3.1 河道概况

滹沱河为海河流域子牙河系两大支流之一,属于季节性河流,河道在枯季常有干涸断流现象,仅在暴雨期间形成河道径流。河床以中细砂为主,渗透性强。黄壁庄水库—北中山河段为滹沱河的主干流,河长约110 km,平均河底比降约为0.051 6%。流经平原,河道宽浅,可以概化为矩形河道。本河段径流主要靠黄壁庄水库泄洪,区间入流可忽略,以河道洪水演算为主。

传统的马斯京根河道流量演算法基于水量平衡对河道洪水进行演算,但对于常年断流、河水与地下水长期处于脱节状态的河道,洪水传播过程中下渗剧烈,渗漏损失量很大,天然状态下洪水演进过程发生显著变化,与模型基本原理不相符[25-26]。所以,考虑渗漏损失的洪水演进模拟成为半干旱地区洪水模拟的关键问题。

3.2 考虑河道渗漏的河道演算方法

目前,河道渗漏损失估算及模拟方面研究已取得了一定成果,国内研究多是直接采用下渗公式方法[27-30]。本文借鉴考虑河道渗漏的分段马斯京根法,对MCT可变参数法和非线性水库法增加河道渗漏计算。采用霍顿下渗公式(式(5))计算每段的下渗率,转化成下渗流量。在入流中扣除后得到每段的净入流量,然后演算到流域出口断面。

ft=(f0-fc)ekt+fc

(5)

式中:ft——下渗率;fc——稳定下渗率;f0——初始下渗率;k——与扩散率有关的系数,与河床的物理特性有关;t——下渗历时。

3.3 河道洪水演算方法的参数率定

由于实测洪水资料比较少,选取研究河段20世纪80年代以后2场典型洪水19880805、19960831进行模拟,探讨考虑河道渗漏的MCT可变参数法和非线性水库法在半干旱区的适用性。洪水的传播时间、输水损失与流量大小、河床干旱程度有较密切的关系。首先根据河道前期干湿状况、河道特性等河段具体情况确定一组模型参数,得出河道下游出流过程,将此过程与河道下游实际出流过程相比较,同时参考下游洪峰流量及起涨点的拟合情况进行综合分析。经过率定,下渗参数fc取5.2 mm/h,k取0.2,f0取1 500 mm/h。将3种演算方法的时间步长定为1 h,河段分为16段,确定河床糙率为0.03,分段马斯京根法x取0.029。

3.4 河道洪水演算结果分析

从表4可以看出:(a)19880805场次洪水3种演算方法的洪峰相对误差均在±20%以内,但都明显偏小;峰现时间模拟结果均较好;确定性系数整体不高。(b)19960831场次洪水的3种演算方法模拟结果均良好。3种方法的洪峰相对误差均在±2%左右;峰现时间模拟结果均较好;确定性系数都大于0.9;整体上MCT可变参数法的精度高于其他2种方法。图2为北中山洪水模拟结果。

表4 滹沱河3种河道洪水演算方法模拟结果

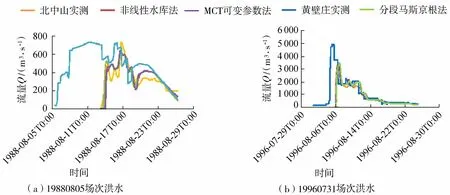
图2 北中山洪水模拟结果Fig.2 Flood simulation results in Beizhongshan

19880805场次洪水模拟结果不好的原因可能有:(a)本场洪水是在河道连续8 a无水的情况下,黄壁庄水库上发生洪水开始放水,河道见水历时长达180 h左右,河道渗漏损失水量约占来水量的52%,输水条件较为复杂,下渗过程模拟比较困难。(b)参数率定过程中侧重于洪水起涨部分的模拟效果,洪峰及落水段没有兼顾好。(c)洪水量级较小,与19960831场次洪水差别较大,且2场洪水时间间隔较长,下垫面因素可能发生变化,下渗条件有所差别,使用同一套参数模拟结果较差。

4 结 语

a. MCT可变参数法基于运动波方程差分解的数值扩散在一定条件下模拟扩散波的物理扩散,能够反映天然河道中洪水波既传播又扩散的运动规律,并引入修正因子保证计算过程中质量守恒和蓄量稳定。本方法考虑了河道断面形状和水力学糙率,参数具有明确的物理意义,对平原缓坡河段的大中型洪水也适用。

b. 非线性水库法在计算过程中考虑了河道断面情况和水力学糙率,在研究河段模拟效果较好,精度和分段马斯京根法相近,具有较强的适用性。

c. 分段马斯京根法计算简便,经验性较强,参数具有一定的物理意义,在研究河段模拟效果较好,具有广泛适用性。

整体来看3种河道洪水演算方法在吴家渡—小柳巷河段的模拟结果均比较满意,精度差异不大。但是,MCT可变参数法和非线性水库法的参数,可以根据河道断面的大断面资料和水力学特性直接估算,考虑河道断面变化对洪水的影响,可以为河道洪水预报提供更多的选择,拓广了现有河道洪水预报方法,同时也为相对复杂的河道洪水预报问题研究提供了一定的参考借鉴。同时本文也在北方半干旱地区初步分析了考虑河道渗漏的3种河道演算方法,模拟结果表明研究思路和方法具有一定的合理性和可行性。鉴于河道洪水预报的复杂性,方法对其他流域的适用性还需进一步论证和检验。