某水电站溢洪道泄水特性数值模拟研究及计算精度验证

杜明松，潘 宇，侯绪亚，邵 凯

(1.江苏江博建设有限公司，江苏 南京 210017；2.南京市水利建筑工程检测中心有限公司，江苏 南京 210017；3.南京河川建设工程有限公司，江苏 南京 210017；4.南京市水利规划设计院股份有限公司，江苏 南京 210017)

我国西部地区地势落差大，水电站溢洪道建设数量多、规模大。但是，水头差高、体量大的发电尾水下泄时，重力势能迅速转换为动能，导致下泄水流流速湍急，流向散乱，对溢洪道稳定运行和下游河床安全都有巨大威胁。因此需要在工程建设前对其泄水水力特性进行系统研究。

目前常用的模拟研究有物理试验研究和数值模拟研究。其中物理试验研究方法应用广泛，研究结论真实可靠，但是工作量大、试验成本高，场地、外界条件等因素的限制程度高。相应的，数值模拟可以很好地解决这一问题，可为溢洪道水力特性研究提供直观、对比充分的研究结论。

本文以四川绵阳某水电站溢洪道为研究对象，采用数值模拟进行计算研究，并借助物理模型试验验证计算精度。

1 实例工程概况

实例水电站位于四川省绵阳市西天寺附近，上距蒋家村22.6km，下离磨刀溪1.3km。设计水位为944.6m，对应的流量为211.3m3/s；校核水位为947.8m，对应的流量为239.5m3/s。

2 三维数学模型建立

2.1 模型建立

本文选择地表河流计算软件中权威度较高的3D- FLOW三维数值模拟软件进行模拟计算。对研究河段进行建模分析，采用有限单元计算模块，网格划分采用三角网格，初始条件通过上游来水量、下游水位、河床糙率、紊动动量传递系数等模型参数进行控制。

2.2 边界条件与初始条件

在二维数模中，边界条件主要包括进、出口边界，岸边界以及动边界等，本模型采用了如下边界条件。

(1)初始条件

对于给定的研究域，在时间t=0时有

h(x，y，t)|t=0=h0(x，y)r(x，y，t)|t=0=r0(x，y)s(x，y，t)|t=0=s0(x，y)

(1)

式中，h0，r0，s0—初始时刻的水位和流量分量。

(2)开边界

r=rB(t)s=sB(t)h=hB(t)

(2)

式中，rB，sB—已知流量过程线；hB—已知水位过程线。

图1 工程模拟范围与计算网格划分

图2 实例工程在各工况下的整体流态分布

2.3 模拟范围及网格划分

本工程的模拟范围包括引渠段、泄槽渐变段、泄槽段、消能段，如图1所示。

3 三维数学模型计算结果分析

3.1 整体流态

实例工程在各工况下的整体流态分布如图2所示。

(1)水流沿着溢洪道固定边界下泄，由于下泄通道较顺直，未出现弯曲段，因此在设计工况和校核工况下，溢洪道断面的水位分布相对均匀，横断面分布有一定偏差，但偏差值较小。

(2)受收缩段出口影响，水流形成较为明显的急流冲击波，在整个溢洪道内不断衍射叠加。对溢洪道的边壁和底板有一定的冲击作用。

3.2 断面水深分布

选择溢0+156和溢0+232两个典型断面，这两个典型断面在设计工况和校核工况下的水位分布如图3所示。

图3 实例工程在各工况下部分典型断面水深分布

(1)在溢洪道中墩出口处，水流受两侧中墩阻挡影响，具有显著的绕流现象。在水流刚经过中墩后，水流在固定边界的引导下，在两侧边壁有一定壅水，并出现一定规模的菱形水流冲击波，整个断面分布呈中间略低，两侧略高的现象。

(2)随着水流进一步下泄，两侧边壁壅水现象逐渐消除，但冲击波波浪规模呈增大趋势。断面水深分布形态逐渐过渡为断面水深分布整体平衡。

4 数值模拟计算结果精度验证

为进一步研究实例工程水力特性，且验证数值模拟计算结果的精确性，本文建立1∶50的正态物理模型试验，进一步计算分析。其中，为更好地观察溢洪道泄水流态，采用透明的有机玻璃板制造溢洪道外墙和底板。物理试验照片如图4所示。

图4 实例工程物理模型试验现场照片(设计工况)

4.1 沿程水深分布

在设计工况和校核工况下，实例工程沿程水深分布如图5所示。

(1)实例工程沿程水面线的数值模拟结果和物理试验校核结果基本一致。其中，泄槽段的水位模拟结果精度最高，引渠段、泄槽渐变段和挑流消能段的水位模拟结果存在一些误差。

(2)引渠段、泄槽渐变段的水位模拟结果误差主要是由水流收缩引起水位的壅高与降低造成的。同时，壅高的水流具有脉动性，水位值一直在变化，给实际测量的精确性造成一定影响，这也导致模拟结果对比值的误差。

(3)挑流消能段的水位模拟结果误差主要是因为水舌最高点和挑距误差比较大，用肉眼观察会存在较大误差，且在该区域水流脉动性更大，测量困难度高。

(4)总体来看，在设计和校核工况下，本文选择10个典型断面，共计350个测点进行计算精度对比。对比结果显示，数学模拟计算值和物理模型实测值的700组对比数据中，最大误差为1.25m，平均误差为0.19m，平均误差率为3.17%；误差值小于0.3m的数据共有544个，占总样本的77.7%；误差值小于0.1m的数据共有398个，占总样本的56.9%。

由此可见，数值模拟结果精度较高，误差率较小，可以较好地反映实例工程的水位分布情况。

图5 实例工程在各工况下沿程水深分布

4.2 脉动压强分布

由于脉动压强测量仪器较难安装且测量仪器设备较昂贵，本文共安排了5个断面，共计15个测点进行脉动压强的测量。其中，各断面测点脉动压强值在设计工况和校核工况下模型计算结果和实测结果见表1。

(1)在15个测点，30组数据中，脉动压强最大误差值为0.29m，平均误差值为0.15m，平均误差率为1.09%。误差较小，数值模拟精度较高。

(2)在水流下泄过程中，未出现负压区域，因此本工程基本不受空蚀影响。

4.3 水流流速分布

根据脉动压强测量分析中布设的15个测点进行水流流速分析。各断面测点流速值在设计工况和校核工况下模型计算结果和实测结果见表2。

(1)在15个测点，30组数据中断面流速最大误差值为0.10m/s，平均误差值为0.03m/s，平均误差率为0.19%。误差较小，数值模拟精度较高。

表1 各断面测点脉动压强数模计算值与物理实验测量值比较

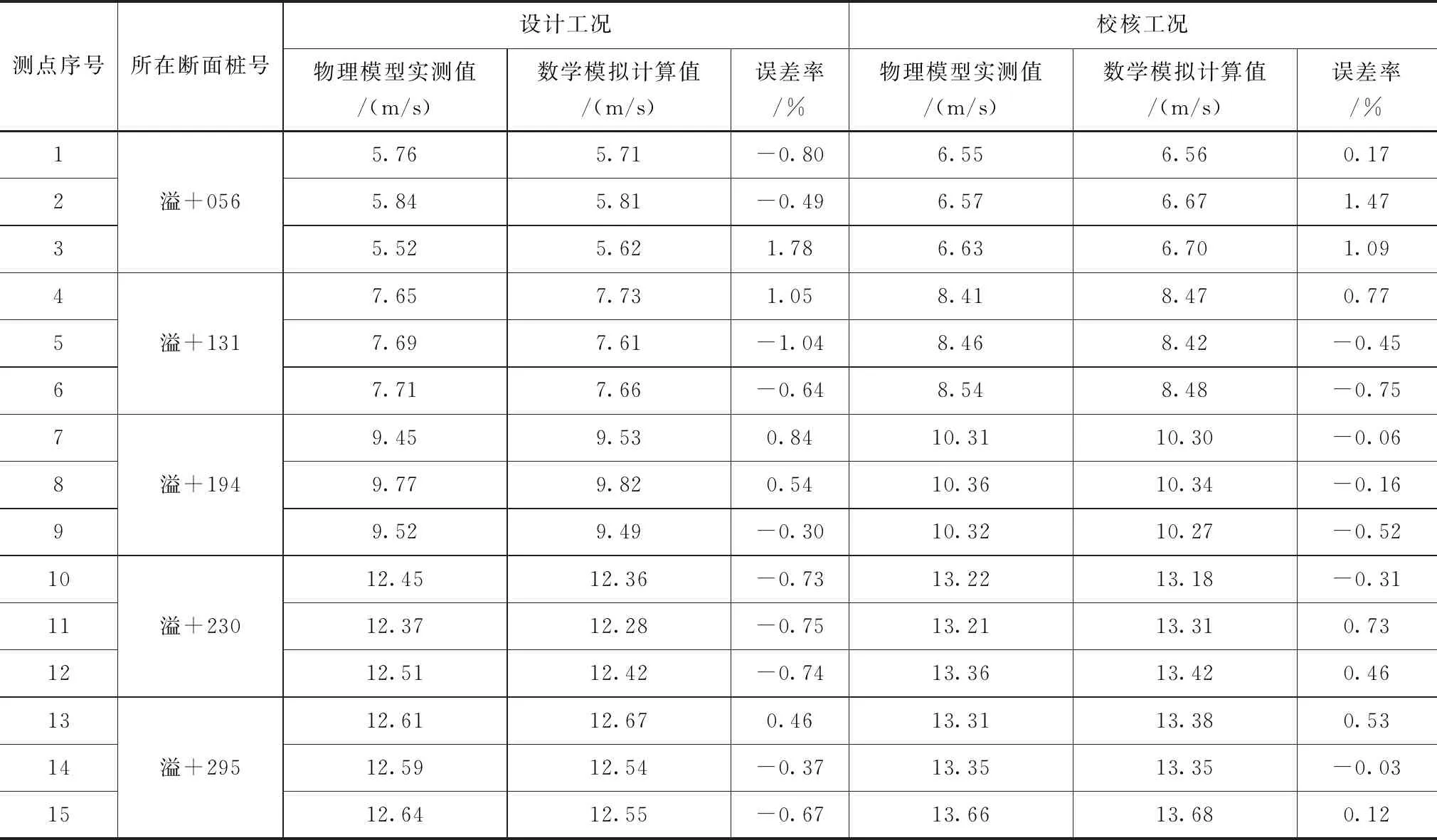
表2 各断面测点水流流速数模计算值与物理实验测量值

(2)经过挑流鼻坎消能，实例工程在设计工况、校核工况下排入下游河床的物理模型实测流速分别为7.95、9.11m/s，远小于规范应不大于20m/s的要求值，因此对下游河床冲刷影响较小。实例工程在各工况下尾水排入下游河床流场图如图6所示。

(3)经计算，实例工程在设计工况、校核工况下消能效率分别为79.13%、84.51%，消能效率较好，工程设计较为合理。

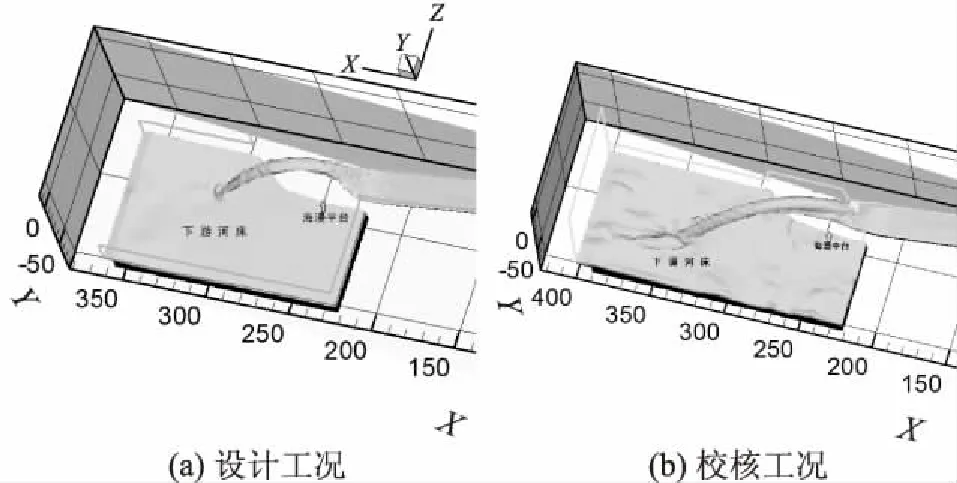
图6 实例工程在各工况下尾水排入下游河床

5 结论

(1)本工程下泄通道为直线渐变段，水流在下泄过程中未受弯道等不利边界条件影响，因此溢洪道断面的水位分布相对均匀，偏差值较小。

(2)在水流下泄过程中，溢洪道底板未出现负压区域，因此本工程基本不受空蚀影响。

(3)经过挑流鼻坎消能，实例工程在设计工况、校核工况下排入下游河床的物理模型实测流速分别为7.95、9.11m/s，远小于规范应不大于20m/s的要求值，因此对下游河床冲刷影响较小。

(4)在各工况下，沿程水深、脉动压强、水流流速分布的数值模拟计算值与实测值较为接近，未出现明显偏差。可见本文建立的数值计算模型能较好地反映实例工程的水力特性，计算精度较高。