基于库水位和蓄水量的土石坝溃决参数预测模型研究

马万龙

(塔城地区水利水电勘察设计院，新疆 塔城 834700)

水库作为水利工程的主要组成部分，在国民经济和社会发展中具有重要的作用和地位。然而，自然灾害特别是暴雨洪水对水库的运行安全存在严重威胁[1]。水库大坝一旦溃决，会对下游地区人们的生命和财产造成不可估量的损失。土石坝以其结构简单、施工方便、造价低等诸多优势，成为大坝建设中历史最久、应用最为广泛的坝型[2]。就国内而言，在已经建成的水库大坝中，有91%属于土石坝。由于其中大多数兴建于20世纪50年代至70年代，设计和建设水平整体较低，因此存在着不同程度的溃坝隐患[3]。

土石坝的溃决过程和预测研究涉及水力学、土力学以及泥沙动力学等诸多学科领域，是一项十分复杂的课题[4]。由于土石坝溃坝实测资料十分匮乏，所以该领域的大多数研究仅可以凭借十分有限的实测数据构建土石坝溃决参数的预测模型，导致模型的预测精度较低[5]。此外，部分研究将土石坝溃决时的溃口宽度作为模型的预测变量，导致模型的应用范围受到极大限制[6]。基于此，本次研究广泛搜集国内土石坝溃决和管涌方面的资料，以上述数据为基础利用多元回归分析法构建以水库的库水位和蓄水量为预测变量的预测模型，以期为土石坝溃决预警和风险评估提供必要的理论支持。

1 土石坝溃决原始数据

研究中通过各种文献平台广泛搜集国内外土石坝溃决实测资料，并对搜集到的资料进行整理和校验，最终建立起涵盖109组土石坝溃决实测资料的数据库。其中有57组漫顶实测数据和52组管涌实测数据。数据库中主要包括发生溃决事故的土石坝的名称、坝型、坝高、洪峰流量、溃口宽度、溃决前的库水位和蓄水量等主要信息。在以往的研究中，案例坝高超过15m的数量较少，而本次研究建立的数据库中，有43组数据的土石坝坝高超过15m，这对于提高研究结果的准确性十分有利。限于篇幅，这里不一一列出所有原始数据。

2 预测模型的构建

2.1 模型的构建原理

回归分析是确定两种或多种变量之间相互依赖的定量关系的统计方法，具有十分广泛的应用。一般来说，回归分析可以通过自变量和因变量与规定实现变量之间关系的确定，建立回归模型，并根据实测数据求解模型的参数[7]。回归分析按照涉及变量的多少，分为一元回归和多元回归分析[8]。其中，多元回归模型的数学表达式如下：

y=β0+β1x1+β2x2+…+βnxn+ε

(1)

由于上式中的参数均为未知，因此需要利用样本数据进行估计，并基于估计结果得到估计的多元回归模型，其数学表达式如下：

(2)

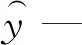
鉴于土石坝溃决前的库水位和蓄水量是最容易获取的数据，将上述两个变量作为预测变量可以快速、及时进行土石坝溃决参数的预测。基于此，本次研究将上述两个变量作为预测变量，基于多元回归分析法建立大坝溃决时的洪峰流量以及溃口平均宽度的预测模型。同时，研究中为了减小不同变量数量级差异对结果的影响，首先对研究变量进行取对数处理。

2.2 洪峰流量

以搜集的57组漫顶溃决案例的实测资料为依据，利用多元回归分析法建立漫顶溃决形式下的土石坝溃决洪峰流量关于库水位和蓄水量的回归预测模型，如图1所示，其数学表达式如下：

lgQp=0.501lgVw+1.093lgHw+0.741

(3)

式中，Qp—漫顶溃决洪峰流量；Vw—蓄水量；Hw—库水位。

式(3)可以进一步转化为如下的幂函数形式：

(4)

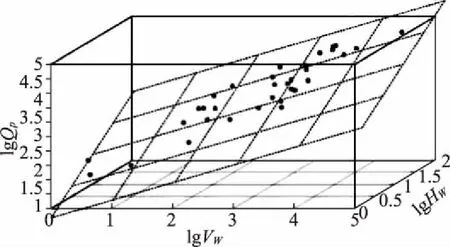
图1 漫顶溃决洪峰流量回归预测模型

以搜集的52组管涌溃决案例的实测资料为依据，利用多元回归分析法建立土石坝管涌溃决形式下的溃决洪峰流量关于库水位和蓄水量的回归预测模型，如图2所示，其数学表达式如下：

lgQp=0.480lgVw+1.019lgHw+0.659

(5)

式中，Qp—管涌溃决洪峰流量；Vw—蓄水量；Hw—库水位。

式(5)可以进一步转化为如下的幂函数形式：

(6)

图2 管涌溃决洪峰流量回归预测模型

2.3 溃口宽度

以搜集的57组漫顶溃决案例的实测资料为依据，利用多元回归分析法建立漫顶溃决形式下的土石坝溃决溃口宽度关于库水位和蓄水量的回归预测模型，如图3所示，其数学表达式如下：

lgBm=0.306lgVw+0.299lgHw+0.640

(7)

式中，Bm—漫顶溃决溃口宽度；Vw—蓄水量；Hw—库水位。

式(7)可以进一步转化为如下的幂函数形式：

(8)

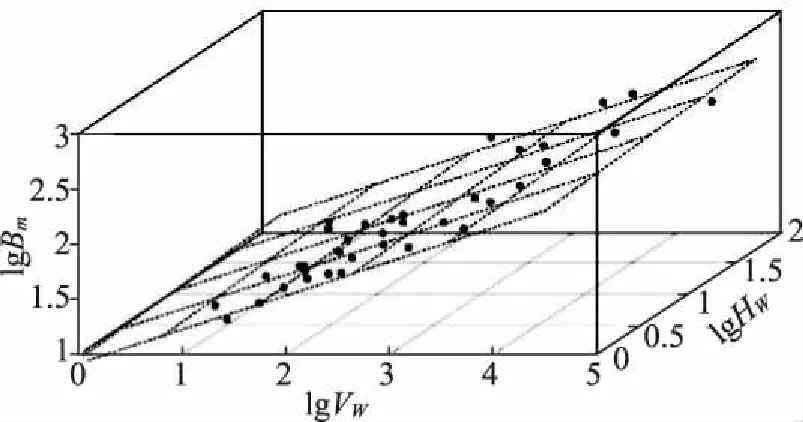
图3 漫顶溃决溃口宽度回归预测模型

以搜集的52组管涌溃决案例的实测资料为依据，利用多元回归分析法建立土石坝管涌溃决形式下的溃决溃口宽度关于库水位和蓄水量的回归预测模型，如图4所示，其数学表达式如下：

lgBm=0.332lgVw+0.060lgHw+0.670

(9)

式中，Bm—管涌溃决溃口宽度；Vw—蓄水量；Hw—库水位。

式(9)可以进一步转化为如下的幂函数形式：

(10)

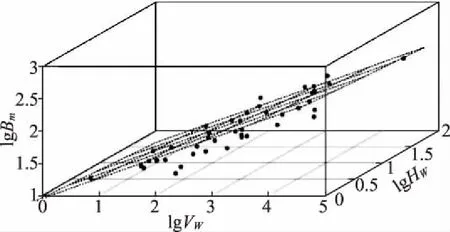
图4 管涌溃决溃口宽度回归预测模型

3 模型的评价与验证

3.1 模型的评价

表1 预测模型评价结果

lgBm=0.342lgVw+0.703

(11)

将式(11)转化为幂函数的形式为：

(12)

式(11)拟合优度的检验结果为R2=0.8365，说明预测模型具有良好的拟合度。鉴于一元线性回归的F检验与t检验是等价的，而显著性检验的P值远小于0.05，说明响应变量与预测变量之间存在显著线性相关关系，具有统计学意义。

3.2 模型的验证

为了验证预测模型在实际背景下的预测精度，本研究选取3组漫顶和3组管涌共6组土石坝溃决案例数据进行模型验证，结果见表2和表3。由此可知，选取的6组土石坝溃决案例中，参数的实测值均位于95%置信区间内，除Lower Otay和刘家台两组案例的溃口宽度预测值与案例的实测值存在一定差距之外，其余案例的预测值和实测值之间均具有较好的吻合度。因此，验证结果显示，本研究提出的土石坝溃决回归预测模型可以实现对土石坝溃决参数的良好预测，具有一定的理论和工程应用价值。

表2 漫顶溃决案例模型验证结果

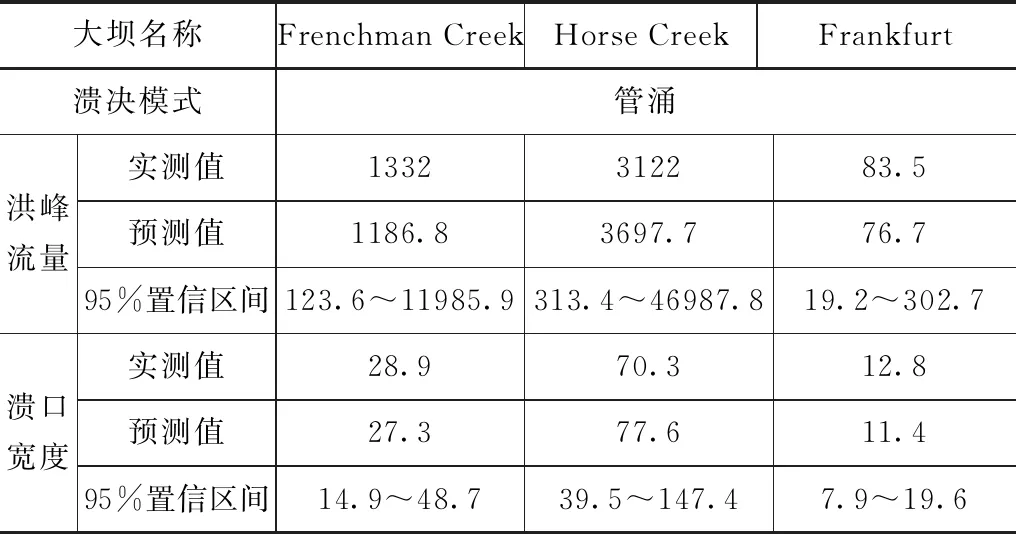
表3 管涌溃决案例模型验证结果

4 结论

本研究基于应用视角选择库水位和蓄水量两个易于测量的水力变量作为预测变量，构建起管涌和漫顶两种不同溃决模式下的洪峰流量和溃口宽度回归预测模型，并对构建的模型进行了评价和验证，获得如下主要结论。

(1)在漫顶溃决时，洪峰流量和溃口宽度与水库库水位和蓄水量之间存在比较显著的线性相关关系；在管涌溃决时，洪峰流量与水库的库水位和蓄水量之间存在显著的线性相关关系，而溃口宽度与库水位和蓄水量之间不存在显著的线性相关关系。

(2)拟合优度和显著性检验结果显示，修正后的4组预测模型对实测数据具有良好的拟合度，同时也具有比较显著的统计学意义。

(3)研究结果和预测模型是基于国内外大量实测数据获得的，具有较高的预测精度，具有一定的理论意义和实际应用价值，可以为土石坝的溃决风险预测和相关预警工作提供参考。