基于ANSYS的某型号平面钢闸门结构振动特性分析研究

董爱玲

(新疆玛纳斯河流域管理局，新疆 石河子 832000)

经济社会的发展离不开水资源的合理调度使用，在一些大型水利枢纽工程中，闸门作为调节控制水流通道的重要设施常常被应用广泛。但不可忽视的是，闸门在工作运营期间，受到水流冲击与闸门自身作用，会发生一定的振动变化，引起闸门结构安全稳定性，因而，研究闸门结构自振特性对提升水利工程安全稳定性设计具有重要意义。国内外已有众多学者研究过闸门在多场耦合作用下自振特性，或采用物理模型试验研究闸门结构布置最佳形式[1- 3]；或基于振动理论分析，研究闸门的振动特性，避免闸门发生碰撞而毁坏[4- 5]；或基于有限元分析方法探讨不同工况下闸门自振特性[6- 7]。本文基于流固耦合理论，利用有限元分析方法，求解多次迭代阶次下闸门自振特性，分析闸门振型特点，结合实际工程，获得流固耦合作用下闸门自振特性。

1 工程概况

某水库是西北某地区农田灌溉、水位调控及工业用水重要水资源调度库，流域面积超过30km2，总库容达到1400万m3，为附近乡镇18万人口提供水资源保障。水库大坝坝顶设计高程为75.30m，长度为15.7m；坝址位于中粗颗粒白云岩基岩上，弱透水性，板状构造，岩体完整性较高；上覆土层主要为第四系风化坡积土，厚度约有6.8m，主要为砂土与粉质黏土，细颗粒结构，距坝顶21.60m处设有大坝宽肩，宽度约为2.1m，作为监测大坝安全稳定性监测平台。根据地质勘察，坝址地下水以白云岩裂隙水为主；坝基稳定，沉降处于安全允许值；坝身并无显著渗漏，安全稳定性经防渗加固后安全运营。

水库枢纽工程还含有溢洪道，主要由溢洪闸作为调水设备，设计方案采用的是3孔8m×6m平面钢闸门，闸室长14.5m，使用混凝土浇筑形成上下游陡坡，坡面分别长9.5、41.2m，坡度为1∶2.25，闸室顶部采用T型钢作为调控机架，并设置有控制机房，启闭溢洪闸，科学合理调控水库水位及水资源。

2 流固耦合振动理论及有限元分析方法

2.1 流固耦合原理

水流过闸门时流固耦合作用的复杂特性，造成闸门系统振动特性发生差异，为此确定流固耦合方程时需要假定理想边界条件[8- 9]，获得的固体作用波动方程为

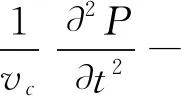
(1)

式中，vc—流体介质中声速；P—声波压力。

引入向量表述离散化函数公式，获得波动方程的离散化向量表达形式：

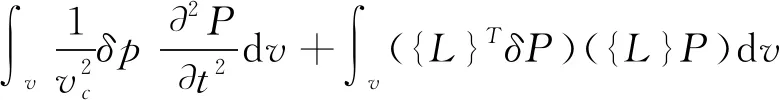
(2)

式中，V—离散化函数积分区域；δP—压力增量；S—流体模量；{n}—边界方向。

根据对流体与结构接触面上动量方程的研究，获得流体水力梯度方程，并联系上述固体作用波动方程，获得矩阵表达式波动方程：

{n}·{P}

(3)

式中，{W}—接触面位移方向。

采用个别分舱治疗，实施常规治疗干预。①升压：关紧舱门，打开供氧阀，调节氧流量，电脑控制均速升压，常规升压时间15 min，升压速率<0.01 MPa/min，必要时根据病人情况，酌情延长加压时间，减慢加压速率。②稳压：病人先吸氧30 min，休息10 min后再次吸氧30 min，吸氧浓度100%。③减压：电脑控制均速减压，减压时间25 min。治疗时注意，对中度耳痛病人应常规暂停3 d～5 d后再行高压氧治疗，或根据病人需要于第2 天治疗前10 min给予羟甲唑啉鼻腔喷雾喷双侧鼻腔，帮助调压。如实施上述措施后病人依旧无法耐受高压氧，则继续暂停治疗，或根据需要行鼓膜穿刺后，再行治疗。

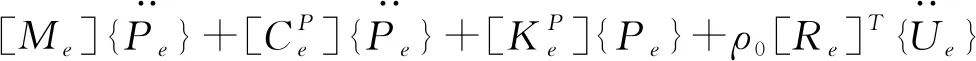
(4)

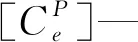
联系流固耦合作用方程，获得：

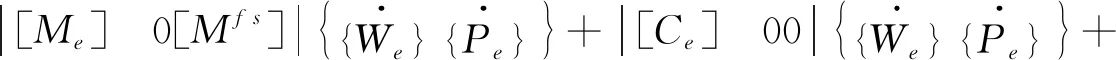
(5)

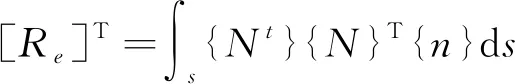
以闸门为分析对象，需要获得其振动模型，由此得到自振频率等特征参数，为研究流固耦合作用下闸门振动特性提供基础，笔者认为闸门结构可离散化多个单元体，分别建立运动方程，即

(6)

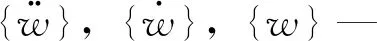
考虑实际水库闸门工况下，闸门的启闭受到水体与结构体耦合作用，获得流固耦合方程的解即可了解到闸门在流固场作用下波动频率及应力变形特征，结合式(5)，划分成微单元体，简化自振运动方程，得到方程及其微分解，即获得平面钢闸门自振频率解集：

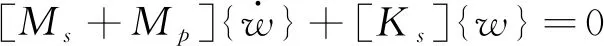
(7)

解集反映了闸门在流固场作用下，闸门波动固有频率变化特征，即ω1，ω2，ω3，…固有频率的振动模态性。

2.2 有限元分析方法

有限元分析方法将闸门划分为多单元体网格的板壳结构，闸门的变形与应力均匀摊铺在板壳结构各个单元体上，如图1所示。

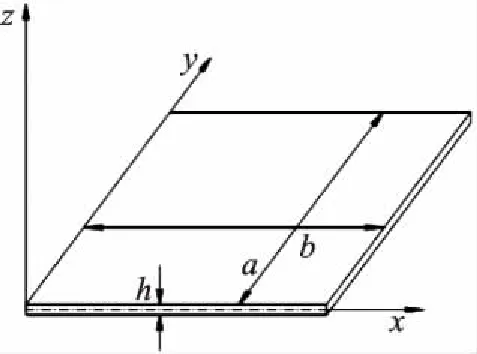
图1 板壳结构单元体

{R}e=[ZiTxiTyiZjTxjTyj

ZmTxmTymZpTxpTyp]

(8)

进而获得单元体的内力与变形矩阵表达式，即

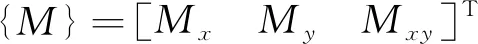
(9)

内力与变形之间的内在联系关系式为

{M}=[D]{χ}=[D][B]{δ}e=[S]{δ}e

(10)

式中，[B]，[D]，[S]—应变、弹性体、应力矩阵。

为了获得流固场作用下闸门振动模态解，需要以微单元体为分析对象，迭代多次，达到收敛，最终获得闸门模态参数特征；而有限元分析方法是单元体网格划分模拟计算精度较高的一种分析手段，本文将借助ANSYS有限元数值分析平台[10]，开展闸门振动特性计算分析。

3 基于ANSYS的平面钢闸门流固耦合振动特性分析

3.1 建模及施加约束条件

笔者借助Solid works构建闸门几何模型，并将模型导入ANSYS软件中，形成数值模型，如图2所示。以Shell 58为单元体，各个单元网格之间呈对称式布置，在纵向与横向方向上均可以施加荷载，符合平面钢闸门在三维空间上受到流体冲击与自身稳定性边界荷载条件的要求。

图2 数值模型图

由于本次研究工况为流固耦合，故对流体(水)进行建模，选用八节点的六面体单元Fiud 28微单元为建模基础，每个流体模型单元体均具有4个自由度，与水流相匹配。闸门物理参数以含碳Q345钢为原材料，其基本物理特性参数作为平面钢闸门基本参数，流体参数按照水的物理学通用标准取值。

有限元分析的重要一步即是模型网格划分，确定合适的网格数量有助于分析解快速达到收敛，利用Hypermesh有限元离散软件，划分出适合本次研究工况的网格单元，如图3所示。边界条件施以基准坐标系，以迎水面闸门中心位置为原点坐标，高度、宽度分别为X，Y轴，水流方向为Z轴。当闸门处于开启状态时，闸门受到闸墩约束；当闸门处于闭合状态时，不仅闸门受到闸墩约束，且闸门底板受到Y轴方向约束。流体选用闸门前迎水侧25m长水流为分析范围。

图3 划分网格单元

3.2 无水工况下闸门自振特性分析

闸门在不同工况下自振特性主要通过多阶参数反映，本文以前6阶模态频率参数及第1、第3、第5、第6阶次振动形态云图开展分析研究。

图4为无水工况下闸门开启与闭合状态下前6阶模态频率参数变化曲线。从图4中可看出，闭合状态下闸门整体自振模态频率高于开启状态，且随着阶次递进，两者之间的差距越来越大，第6阶次闭合状态下闸门自振模态频率是开启状态下的1.5倍，而第1阶次闸门开启与闭合状态下模态频率近乎接近，表明迭代阶次越深入，闸门开启与闭合状态下模态频率差异越大，笔者分析是由于闭合状态下闸门受到闸室底板约束的影响。从闸门关闭状态变化曲线来看，随着迭代阶数增长，模态频率逐渐增大，且增大幅度越发显著，第3阶次相比第1阶次，模态频率仅增长了7.9%，而第6阶次比第5阶次却增长了70.3%，这种现象同样与在闸门开启状态下类似，表明闸门的模态频率均随着迭代阶次增大而逐渐增长至较高水平。

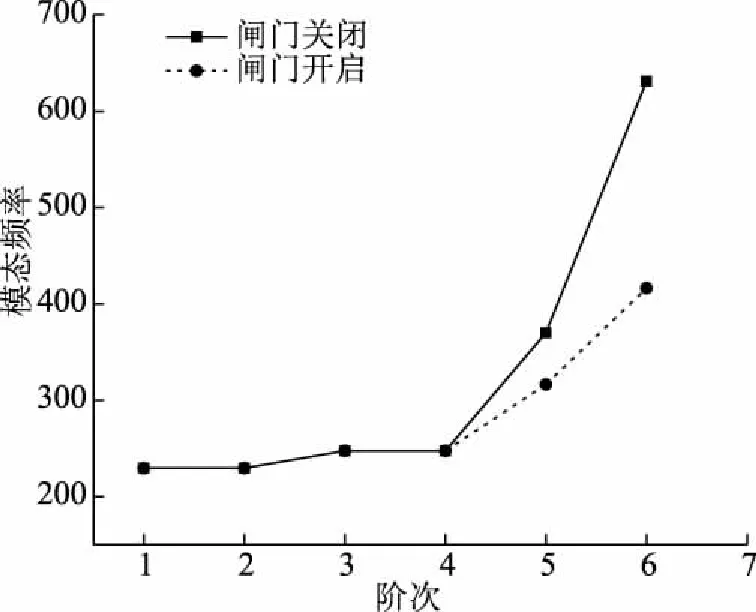
图4 闸门开启与闭合模态频率参数变化(无水工况)

图5为无水工况下闭合与开启状态下闸门自振振型云图。从图5中可看出，闭合状态下闸门整体振型变化不大，迭代阶次较低时，闸门主要在背水侧发生部分振动变化，迎水侧并无较显著振动；随着迭代阶次增大，振动区域在背水侧主要集中在板体中间。闸门开启时自振振型与闭合时差异主要体现在迭代阶数较高时，当迭代阶数达到第5与第6阶次时，开启状态下闸门自振振型主要体现在闸门板体上部与中间区域，这也主要是因为与开启状态下闸门仅受到闸墩约束，顶底部方向上并无约束，故而闸门扭转摆动幅度出现在该区域。

图5 无水工况闸门闭合与开启下自振振型云图(从左至右依次为第1、第3、第5、第6阶次)

3.3 流固耦合下闸门自振特性分析

图6为流固耦合作用下闸门在不同开启程度下各迭代阶次模态频率变化曲线。从图6中可看出，流固耦合下闸门关闭时模态频率近乎与无水工况下一致，两者之间差异较小；当闸门在开启状态下，在同等迭代阶次条件下，开启角度越大，模态频率越大，但这种增大现象仅在迭代阶次超过5时才显著，第6迭代阶次时，闸门开启90%相比闸门开启25%时增长了7.8%，模态频率达到412.3；与无水工况下类似，开启程度保持恒定时，随着迭代阶次的增加，闸门模态频率逐渐增加，且迭代阶数愈高，增长越明显，闸门开启25%时，第6阶次相比第5阶次增长了41.1%，而当闸门开启90%时，第6阶次相比第5阶次增长了30.7%，表明闸门开启程度越大，闸门模态频率增长速率降低。

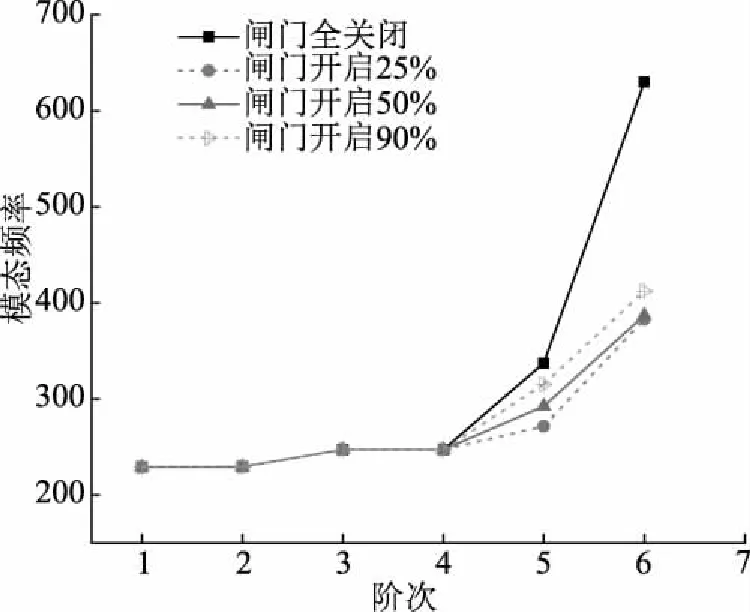
图6 模态频率参数变化(流固耦合)

图7为流固耦合条件下闸门不同开启程度时各个迭代阶次自振振型云图。从图7中可看出，在较低迭代阶次时，不论是闸门全关亦或是闸门开启90%，其振型云图近乎一致，当迭代阶次超过5时，闸门开启程度越大，闸门背水侧顶部及板面中间区域振型变化显著，但变化幅度较小。这主要是由于迭代阶次越大，对振型收敛度要求愈高，反映在闸门上则是受水流冲击作用，闸门振型分布发生变化，但振动幅度显著降低，闸门开启90%时振动幅度最大，仅有0.148×10-4，相比全关状态下减少了2个量级，由此表明，闸门开启程度增大，迎水侧水位降低，流体与钢闸门接触面积减小，闸门振动幅度降低。

图7 流固耦合不同开启程度下自振振型云图(从左至右依次为第1、第3、第5、第6阶次)

4 结论

(1)无水工况下闸门闭合时模态频率高于开启时，随阶次递进，差距愈大，第6阶次闭合模态频率是开启时的1.5倍，而第1阶次两者近乎接近。随着迭代阶数增长，闸门开启或关闭下，模态频率均是逐渐增大。

(2)无水工况下闸门自振振型变化幅度较小，迭代阶数超过5时，振动变化主要出现在闸门板体上部与中间区域。

(3)流固耦合下闸门关闭模态频率与无水工况下一致；随着闸门开启角度增大，模态频率越大，迭代阶次越大时越显著，闸门开启90%模态频率达到412.3；闸门在同等开启角度下，随着迭代阶数增大，模态频率增大。

(4)在较低迭代阶次下，闸门全关或闸门开启，振型云图近乎一致，只有当迭代阶次超过5时，闸门背水侧顶部及中心部位才随闸门开启程度增大而逐渐发生显著变化，但变化幅度较小，门开启90%时振动幅度最大，仅有0.148×10-4，相比全关状态下减少了2个量级。