基于RGRS的空域划设问题研究

文 秘，方 强，黄兴龙，张一鸣

(1.空军指挥学院 研究生大队，北京 100097；2.中国人民解放军66133部队，北京 100097)

空域划设问题直接关系到空域使用效率和安全，从而影响作战效能和经济效益，不论在军航还是民航都是研究的热点。目前，空域划设主要有两种思路[1]：一是从上向下划设，以基于最优化理论的“排样”法为典型代表。该算法将空域划设问题抽象为一个多维“下料”问题，结合最优化算法，得到空域划设方案。二是从下向上划设，以网格“生长”算法[2-3]最为突出。该算法是在空域离散化的基础上，从初始生长点，按照一定的信息素条件进行临近生长，直至实现空域的完全划分。两种思路各有其特点。近年来，网格“生长”算法由于更贴近划设实际、算法过程明晰等特点，得到了更广泛应用和研究。

一般的“生长”算法[4-5]，网格选择任意,缺乏实际意义，不能与地图相匹配，信息素收集困难；且生长网格没有嵌套效应，需专门设计边缘平滑算法。弧度制全球网格系统，用等弧度划分替代等角度划分，用十进制代替六十进制，采用单一尺度均匀划设而非多尺度划设，形成了以网格为单元的全新地理空间计算和管理框架，极大地简化了空间计算。基于弧度制网格剖分的改进“生长”算法，信息素收集方便，使用算法嵌套平滑边缘，能极大提升空域划设效率。

1 弧度制全球网格

全球网格参考网格系统是一种科学的、简明的、全球统一的刚性定位网格参照系统，比较常见的是MGRS和GARS[6-7]。MGRS与GARS网格系统，在目标定位和区域协同方面各有其优势，但存在共同缺陷：① 采用角度制，计算复杂。角度制是一种六十进制的计数方法，与日常生活的十进制区别较大，带来计算和认知麻烦；② 划分具有多尺度效应。两种网格都是等度、等分、等秒划设，但间隔尺度不一。如在GARS中，划分为30′、15′和5′的3个层级[8-10]，实现网格向下 “四等分”和“九等分”，这种尺度差异给跨网格(空域)组合和拆分带来极大的困难。弧度制网格参考系统，采用弧度制和“百等分”方法，将角度和距离统一起来，并实现十进制计算，克服了MGRS与GARS网格系统的不足。

1.1 弧度制网格构建

弧度制网格系统，按照“确定地图基础和坐标系——确定划分规则，进行全球划分——确定编码规则，对剖分进行编码”的步骤进行网格系统构建[11，12]。

1.1.1确定地图基础和坐标系

以经纬度坐标体系为依据，采用圆柱投影中的横轴墨卡托投影，按照西经180°经线展开形成平面地图为划分基础，它的坐标范围为：西经180°至东经180°；南纬90°至北纬90°，将其转换为弧度制为：经线(-π,π)；纬线(-π/2,π/2)。若以180°W90°N(南极点)为原点，180°W经线方向为y轴，垂直于180°W经线方向为x轴，建立平面直角坐标系，则相应的坐标范围变为：x轴方向(0,2π)；y轴方向为(0,π)，如图1所示。由于π值近似等于3.14，因此坐标范围又可描述为：x轴方向(0,6.29)；y轴方向为(0,3.15)。

图1 弧度制坐标系统

1.1.2确定划分规则，进行全球划分

弧度制网格剖分，以原点为起点，向东和向北，按照0.01 rad×0.01 rad进行划分，形成628×314个一级网格，网格大小为64 km×64 km。依次对上一级网格进行10×10等分，形成第二、三、四、五、六级网格(见图2)，后一级网格尺寸是上一级尺寸的1/10，面积为1/100，维持十进制关系。弧度制能使角的集合与实数集合R存在一一对应关系，一个完整的圆的弧度是2π，即2π rad=360°，因此1 rad=57.3°。弧度制不仅能将角度和距离度量统一到十进制，而且能够极大的简化弧长(距离)的计算：L=α(弧度)×R(半径)。

图2 RGRS剖分及编码示意图

1.1.3确定编码规则，对网格进行编码

按照弧度制网格剖分规则，全球可划设628×314个一级网格。一级网格编码按照“序号不足三位补足三位数”的编码规则，构成XXX-YYY的结构，则网格坐标轴范围为：纬线方向000～628；经线方向000～314。如图2中阴影部分的一级网格的编码为“627-309”，二级至六级编码，按照“10×10”坐标点的方式进行“分层—交叉”编码，图2中的二级编码为“2-3”，三级编码为“8-6”，则一个完整的精确到三级网格的编码为“627-309-2-3-8-6”，亦可简写为“627-309-23-86”。

1.2 网格信息素矩阵

地球是一个椭球体，两极稍扁，赤道略鼓，半径长度均值约为6 400 km，由此可得弧度制全球网格系统基础网格层级及精度，见表1。一个完整的网格编码长度等于“4+2×级数”，第六级网格的完整编码有16位，通常划分到三级(10位)，区域精度为“640 m×640 m”，已经能够满足绝大多数区域定位和协调需求。

表1 RGRS基础网格层级及精度

以不同精度的弧度网格作为存储空间数据的“抽屉”，把多源异构数据规则地放置到“抽屉”中，不同数据之间通过网格编码有机地关联在一起，由此可实现多源异构数据在空间特征上的关联整合，这些“抽屉”和信息数据共同构成了网格信息素矩阵。在图2中，弧度制全球网格参考系统的一级网格，构成了一个628×314的信息素矩阵A；二级网格构成了一个6 280×3 140的信息素矩阵B；三级网格构成了一个62 800×31 400的信息素矩阵C。

(1)

式(1)中：∀i∈[1,618];∀j∈[1,314]; ∀k,l∈[1,10]；sum+(·)算子表示信息素矩阵所有元素值求和。利用多颗粒度的信息素矩阵，能够实现区域定位和数据的存储计算。

2 弧度制网格空域划设

区域生长算法[2-3]，是一种经典的基于区域的图像分割方法，是一种根据事前定义的准则将像素或子区域聚合成更大区域的过程，其实质就是按照一定的规则(如性质相似)把像素连通起来，从而最终构成分割区域。本文中将区域生长算法应用到空域划设，将弧度网格单元统计数据(信息素)作为“像素值”。

2.1 空域划设数学模型

空域生长算法是从初始点网格出发，向四周不断的生长合并其他网格，最终实现对区域网格的完全划分。划分的过程中始终坚持各划分区域之间信息素均衡。由此可得，基于弧度网格的空域划设数学模型为：

MIN=VAR(Zi)

s.t.

(2)

式(2)中：i表示优化划分的第i个区域；j表示空域内第j个网格单元；n表示空域内的所有网格单元个数；m表示区域划分总数；Ni表示与网格单元j相邻的网格单元集合；xij∈{0,1}表示网格单元j是否属于区域i；yi∈{0,1}表示存在第i区域输出时为1，否则为0；Zi表示第i个划分区总信息素。

目标函数表示各划分区块信息素应当均匀；约束条件1确保了每个空域网格单元只能归属于一个分区，即反映了分区不能交叉重叠，也不能留有空隙的约束；约束条件2确保所划分的分区大小和形状合理；约束条件3确保扇区内所有网格单元是相连的，满足了分区连续性约束；约束条件4保证所有网格单元被划分出去，不会有剩余网格存在。

2.2 改进区域生长算法

区域生长算法是建立在区域网格化的基础之上，有三个关键步骤[4-5]：

1)种子点的选取。选择一组能正确反映所需区域特征的点。一是种子点的数目m，即空域划设的数目；二是种子点的位置，该问题可选择航迹点密度最大的前m个网格作为种子点或者随机选择。

3)确定区域生长的终止原则。所有的网格都分配完毕。

以基于航迹点密度的空域分割为例，改进生长算法的具体步骤为：

步骤1根据划设区域范围，建立划设区一级网格坐标系统；根据划设精度，确定弧度网格最终等级Num；

步骤2统计当前等级网格系统中，每个网格的信息素，确定划设分区数目及相应初始生长点；

步骤3从每个初始点所在单元网格出发，搜索相邻单元网格中信息素最小的网格，并将其信息素与相应生长点的信息素相加，形成待生长区；

步骤4比较各待生长区总信息素，找到其中信息素最小的待生长区，合并其网格及信息素，作为下一轮生长的初始生长点，释放其余待生长区；

步骤5重复步骤3、步骤4，直至找不到还未分配网格，完成该级网格划分；

步骤6判断网格等级是否达到Num；若没有达到网格等级要求，则根据该级网格划分确定的划分边界，依次对每一个边界网格10×10剖分，形成下一级网格坐标系统，选出该系统中最靠近相应分区的点作为新的生长点，转到步骤2；若达到网格等级要求，转到步骤7。

步骤7对网格边沿进行平滑，完成空域划设。

假设任意网格单元为Bij，共N个；分为M个区块；每个区块的种子单元为Zijk,k∈[1,M]；第k个区块集合为Qk，显然Zijk⊂Qk；第k个区块的临近区块集合为Lk={与k区块相邻且未分配的Bij}，Bijk表示集合Lk中信息素最小的网格，则一个层级网格的算法流程如图3所示。

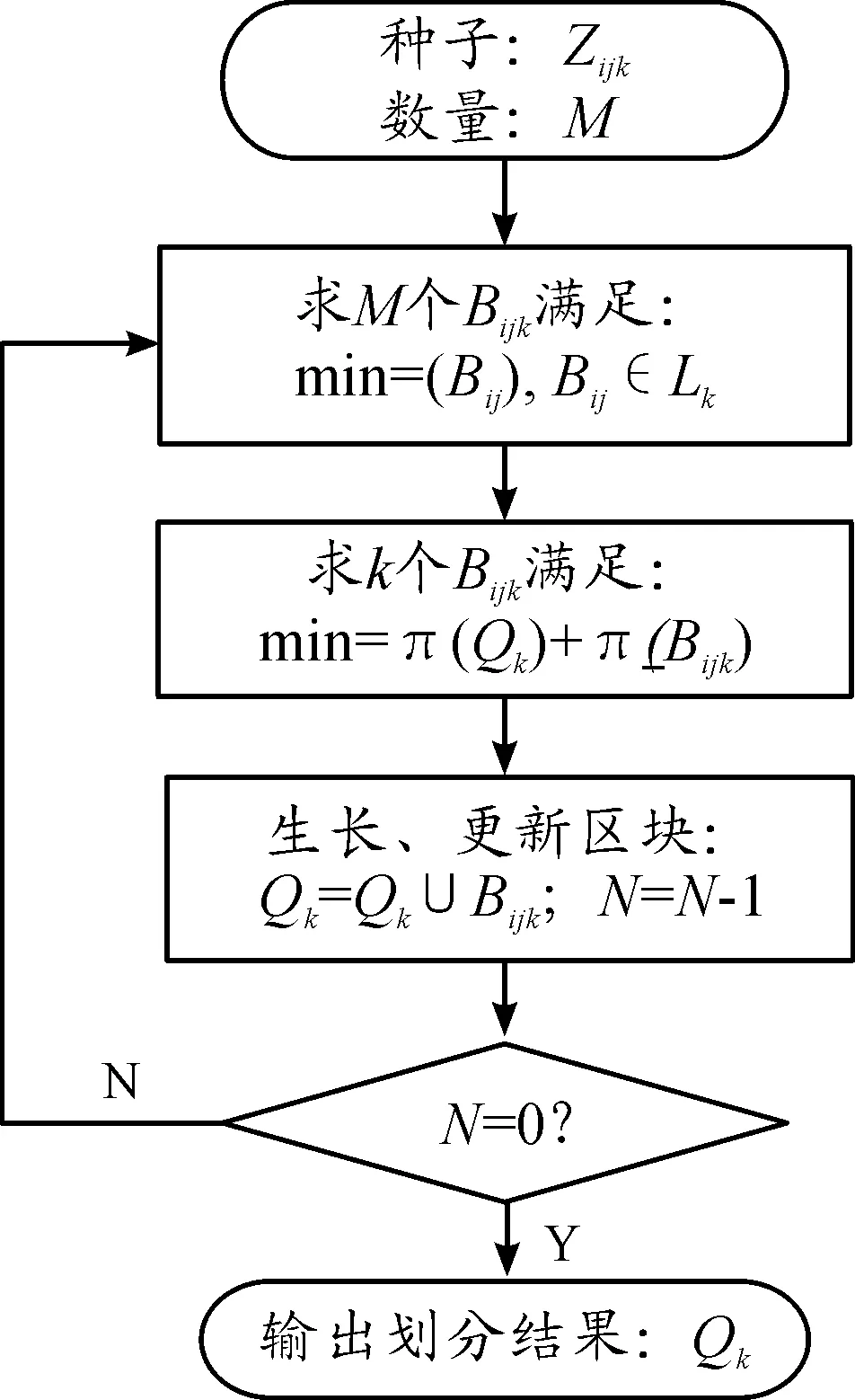
图3 改进生长算法流程

由算法步骤和流程图，得到改进生长算法与原生长算法[2-3]，见表2。

表2 改进生长算法与原算法

3 空域划设仿真

以某地区空战场管制空域划设为例，该空战场覆盖的区域是一个由A1～A5(顺时针)五个顶点构成的多边形区域，各顶点的经纬度坐标已知，则按照弧度制网格编码规则能够计算出对应的网格编码，见表3。

表3 区域顶点坐标及所在网格编码

按照弧度制剖分规则，进一步将待划设的对多边形区域进行栅格化，形成13×13个一级网格组成的栅格化区域，精确度为64 km×64 km，如图4所示。

根据作战计划，特别是航迹规划信息，可以得到航迹点统计数据，由于保密原因，以随即产生一组信息素矩阵A为条件进行仿真实验，表4为一组随机信息素矩阵A数据。

图4 多边形区域及栅格化

表4 信息素矩阵A13×13

随机选择A(3,4)(对应弧度网格519-213)、A(6,11)(对应弧度网格526-210)、A(8,9)(对应弧度网格524-208)三个点，作为初始生长点(表3中被框选的位置)，按照2.2节的改进生长算法进行空域分割。

经过一次空域生长，得到了一个大体的分区划设结果，如图5所示。显然，该结果并不能满足分区空域满足凸约束的条件，因此需要对其边缘进行调整。将三部分空域区块的边缘部分网格进行向下一级剖分，每个网格重新形成10×10个二级网格，精确度为6.4 km×6.4 km，然后按照2.2节的改进生长算法对每个边缘网格再进行一次空域分割，并进行边缘平滑，得到最终的分区划设结果，如图6所示。

图5 一级网格尺度下空域分区划设结果

图6 边缘平滑及最终分区

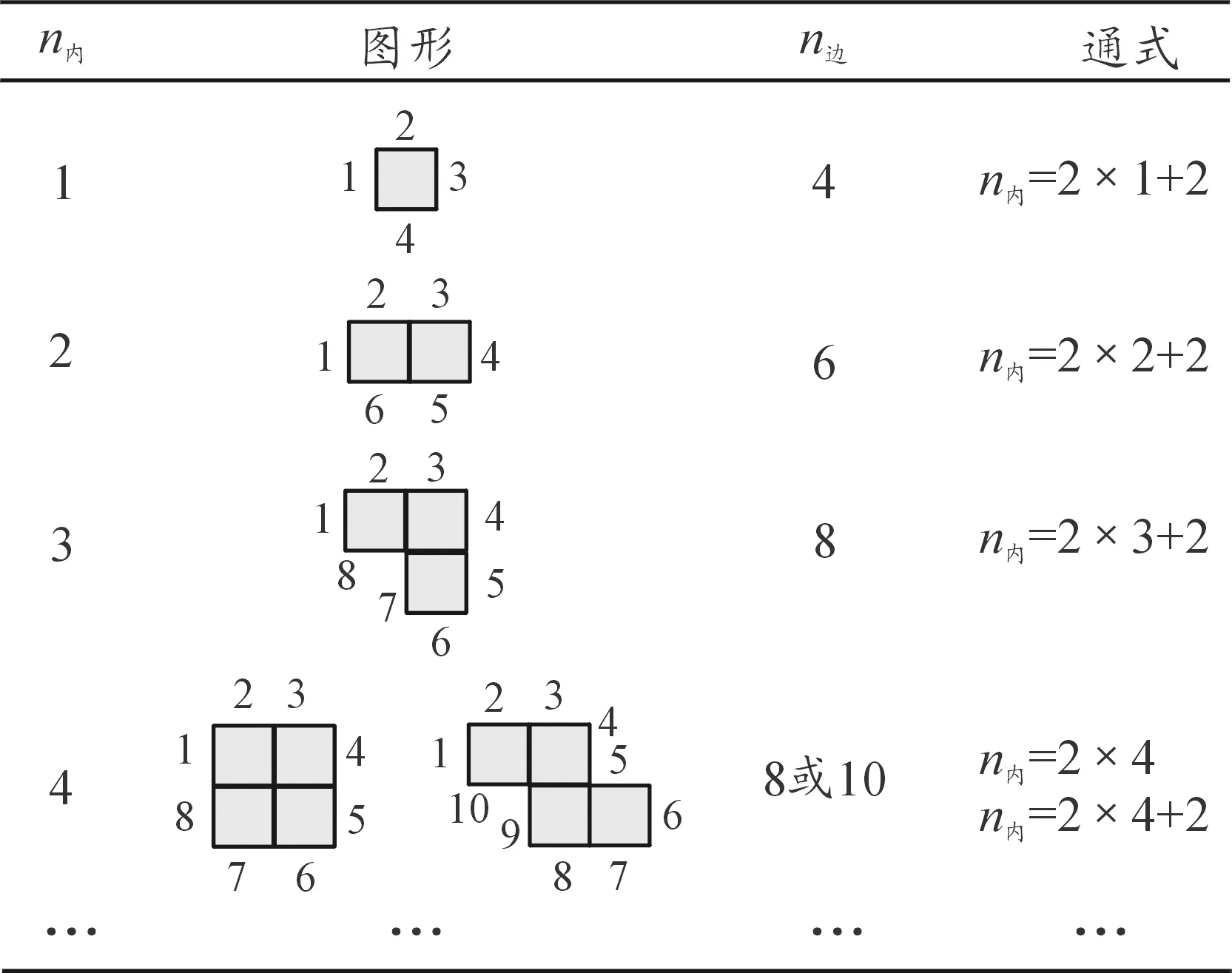
由生长算法的流程可以看出，算法复杂度和对于系统资源的消耗主要集中在本文2.2节步骤3(改进算法与原算法共有)：搜索生长区边界最小信息素单元网格。以按照四个方向生长为例，可以归纳统计出边界单元网格数目n边与区域内部网格数目n内的关系，如表5所示。

由表5可以得到：n边≥2n内，当n内较大时n边≈2n内。从初始生长点生长到n内网格点的区域的过程中，需要进行的边缘搜索的总次数为：S=n内(n内+1)。若待生长区域总网格数为n，区域划分块数为N，每个区块所包含的网格数为n/N，则区域划设总边缘搜索总次数为：n2/N+n，对于一个固定的问题N为定值，则该算法的复杂度由n2/N决定。因此，对于本文空域划设问题，提升效率的计算方法如下：

(3)

式(3)中：ρ表示提升的划设效率；λ内表示多边形内网格数量；λ边表示多边形内部各分区之间的边界所包含的网格数量；乘数100表示将当前网格划分为100个次一级网格。在该问题中划设效率大概提升了90.4%，效果明显。

表5 边缘网格数目计算

4 结论

本文提出了基于弧度制的全球网格系统，并将其应用于空战场管制空域划设。利用弧度制网格参考系统的全球剖分、十进制和多颗粒度特性，对空域划设生长算法进行了改进。仿真实验表明，该方法信息素收集方便，嵌套平滑边缘，能够极大的提升空域划设的效率。