弹丸侵彻陶瓷/钢复合靶板数值研究

刘润华,陈国光，侯 飞，黄书伟，张岚清

1.中北大学 机电工程学院，太原 030051；2.中国兵器工业第208研究所，北京 102202)

21世纪以来，反装甲武器的毁伤效能越来越高，传统的“厚”、“重”装甲防护材料不能满足现代战争的需要。装甲防护材料必须具有一定的防护性与机动性能，陶瓷材料有着耐磨蚀、耐高温、低密度的物理性能,陶瓷复合装甲可以集中组元材料的优点，在满足装甲的防护性能的同时又降低装甲重量，因此研究陶瓷复合靶板抗侵彻性能具有重要意义[1-2]。国内外许多学者进行了陶瓷复合靶的研究，匡格平[3]研究了弹丸高速撞击陶瓷/金属复合靶特性，认为陶瓷/金属复合靶板的防护性能高于非复合的金属靶板；王长利等[4]进行了爆炸成型弹丸对陶瓷材料的侵彻研究，认为陶瓷材料可以提高装甲抗侵彻性能；Den Reijer[5]认为复合靶板的钢背板对陶瓷靶板有支撑作用，提高了陶瓷靶板的抗侵彻性能；焦志刚等[6]进行了陶瓷复合靶板抗侵彻性能数值仿真的研究，认为复合靶板能够提高抗侵彻性。尹志新等[7]分析了隔层以及多层结构对陶瓷/金属复合靶抗侵彻性能的影响，认为复合靶的厚度配置是影响其抗侵彻性能的关键因素；M.Lee等[8]采用SPH方法较好的分析了弹丸侵彻陶瓷/金属复合靶板的侵彻机理。

以上研究主要集中在陶瓷复合靶材料、层数、排列顺序等对其抗侵彻性能的影响，未涉及有无间隔对陶瓷复合靶抗侵彻性能的影响研究。作者采用LS-DYNA有限元分析软件，建立弹、靶模型，进行数值模拟，结合仿真结果，获得陶瓷/钢复合靶有无间隔对其抗侵彻性能影响的规律，为装甲防护材料的结构优化提供指导。

1 建立模型

建立合理有效的弹丸侵彻陶瓷/钢复合靶板有限元模型，是正确分析陶瓷复合靶板抗侵彻性能的前提。弹丸垂直侵彻陶瓷/钢复合靶板，使用三维Lagrange计算方法，网格划分采用3D-Solid-164；在弹靶模型对称接触面定义对称边界条件；在靶板模型边界定义非反射边界，消除反射应力波对模型计算产生的干扰；弹丸与靶板、靶板与靶板之间的接触算法均采用面面侵蚀接触算(*CONTACT-ERODING-SURFACE-TO-SURFACE)；建模单位采用cm-g-μs。

1.1 建模分析

弹丸和钢靶板本构模型采用JOHNSON-COOK模型，陶瓷靶板的本构模型采用JOHNSON-HOLMQUIST-CERAMICS模型(也称JH-2模型)，作者用于侵彻仿真实验的相应材料参数如表1、表2所示。

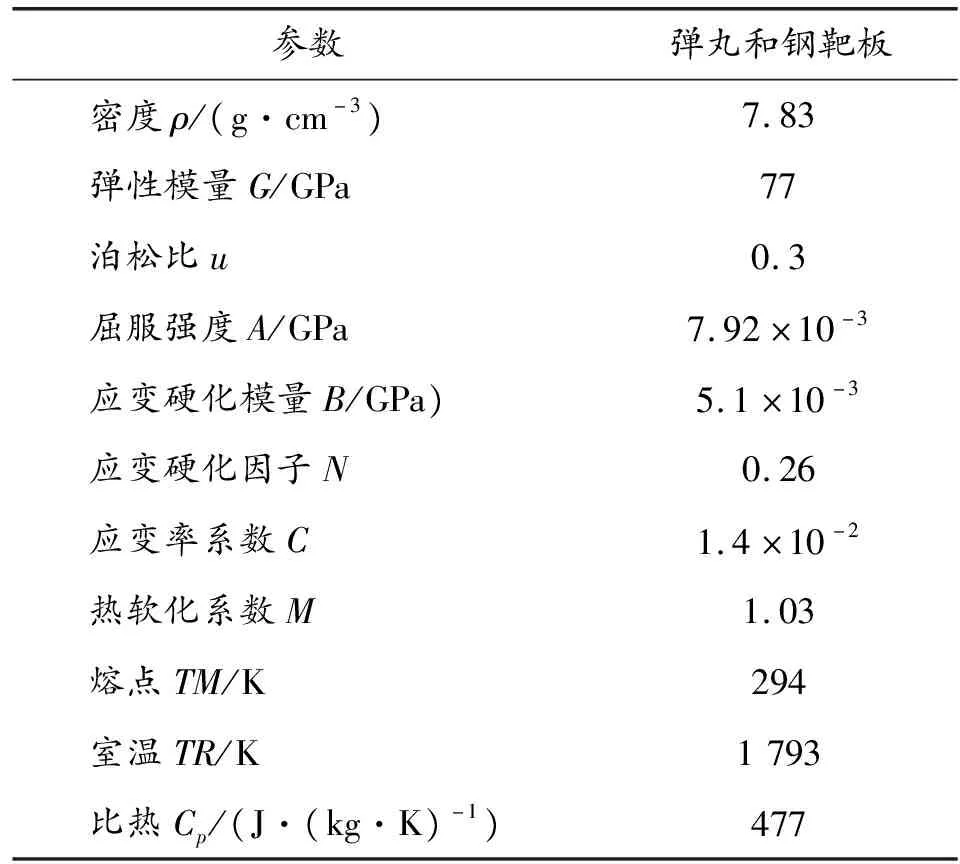
表1 弹丸和钢靶板材料参数[9-10](JOHNSON-COOK模型)

JOHNSON-COOK模型也被称作粘塑性模型，适用于材料在高温、大变形下的工程问题求解。材料在侵彻下的Von-Mises流体应力表达式为[11]：

表2 陶瓷靶板材料参数[12-13](JH-2模型)

JOHNSON-HOLMQUIST-CERAMICS模型也称JH-2模型，适合描述陶瓷、玻璃等脆性物质的破坏形式，可以计算脆性物质的损伤程度，其表达式为[11]：

σ*为等效应力；

陶瓷材料无损时的强度表达式：

陶瓷材料破损时的强度表达式：

损伤因子D定义为累计塑性应变与失效应变之比，

1.2 建立有限元模型

弹丸为半球形头部、圆柱弹身结构，直径为2.6 cm，长度为4 cm，弹丸初速800 m/s,垂直侵彻陶瓷/钢复合靶板。为减小靶板尺寸和边界约束对弹丸侵彻分析的影响，可将陶瓷靶板尺寸和钢靶板尺寸均设计为15 cm×15 cm×1 cm。

为分析陶瓷复合靶各层之间有无间隔对其抗侵彻性能的影响，在弹丸侵彻无间隔复合靶板实验组的基础上建立两组弹丸侵彻有间隔复合靶板对照组。无间隔复合靶板各层靶板紧密相连，两组有间隔复合靶板各层间隔分别为2 cm、4 cm，仿真实验中靶板间隔是指第一层靶背面到第二层靶正面的距离。侵彻仿真实验具体分组如表3所示。

在有限元分析中，计算精度会随着网格数量增多而提高，但计算用时也会增大，因此可在关键部位增大网格密度以提高计算精度，在次要部位降低网格密度以缩短计算时间节省资源[14-15]。综合考虑侵彻结果精度、计算时间、计算机处理能力，本文在对弹丸和陶瓷/钢复合靶板进行网格划分时，在弹丸和靶板接触区域即靶板中心，细化网格以保证计算精度，在距离靶板中心较远的区域，疏化网格以提高计算效率。由于有限元模型关于弹丸纵轴对称，将其简化成四分之一模型以节省计算时间；弹丸和靶板单元类型选用3D-Solid-164八节点六面体单元，陶瓷靶板和钢靶板网格最小尺寸1.5 mm×1.5 mm×1.0 mm，模型共划分 53 008个单元，其中弹丸 3 008个单元，陶瓷靶板和钢靶板均为25 000个单元。

表3 侵彻仿真实验分组

弹、靶有限元模型如图1 所示，其中图1(a)、图1(b)分别是弹丸侵彻无间隔陶瓷/钢复合靶板和有间隔陶瓷/钢复合靶板有限元模型。

图12 弹丸侵彻陶瓷/钢复合靶板有限元模型

2 仿真结果与分析

2.1 弹丸侵彻速度变化

对弹丸侵彻速度的研究一直是分析高速撞击问题的重点，而剩余速度是衡量弹丸的贯穿能力和和靶板的抗侵彻性能的重要指标之一。图2分别为弹丸侵彻无间隔陶瓷-钢复合靶板、间隔2 cm陶瓷/钢复合靶板、间隔4 cm陶瓷/钢复合靶板时弹丸侵彻速度的时间时程曲线。

从图2可以看出：在侵彻的初始阶段，弹丸接触陶瓷靶，弹丸速度近似线性地变化；随着侵彻时间的推移，在弹丸击穿陶瓷靶之前，弹丸的侵彻速度衰减变缓；弹丸击穿陶瓷靶板后到达陶瓷/钢结合面，弹丸侵彻速度急剧衰减；弹丸击穿钢靶板后，弹丸侵彻速度基本不变，此时的速度定义为弹丸的剩余速度,剩余速度能够直观反应靶板的抗侵彻性能。

图2 三组侵彻仿真实验弹丸速度时程曲线

从三组仿真实验的弹丸速度曲线分析，弹丸击穿陶瓷/钢复合靶板后弹丸的剩余速度分别为435 m/s、464 m/s、466 m/s，弹丸动能损失分别为46%、41%、41%。数据表明，弹丸侵彻无间隔陶瓷/钢复合靶板的弹丸剩余速度最小，主要是由于无间隔陶瓷/钢复合靶钢背板对陶瓷靶板存在支撑作用，提高了无间隔复合靶板整体抗侵彻性能。

2.2 弹丸加速度变化

对弹丸加速度变化分析，可以为靶板的抗侵彻性能研究提供参考。图3所示为三组侵彻仿真实验弹丸加速度时程曲线。侵彻初期弹丸接触靶板，弹丸加速度曲线出现第一个峰值；当弹丸侵彻至钢靶板时，弹丸加速度骤然增大，并且弹丸侵彻无间隔复合靶的加速度要大于弹丸侵彻有间隔复合靶时的加速度。弹丸在侵彻钢靶板的过程中，弹丸和钢靶板的形变过程以及相互之间的影响较为复杂，且弹丸加速度变化无法通过仿真实验准确分析，因而作者仅分析弹丸开始侵彻钢靶板时弹丸的加速度。

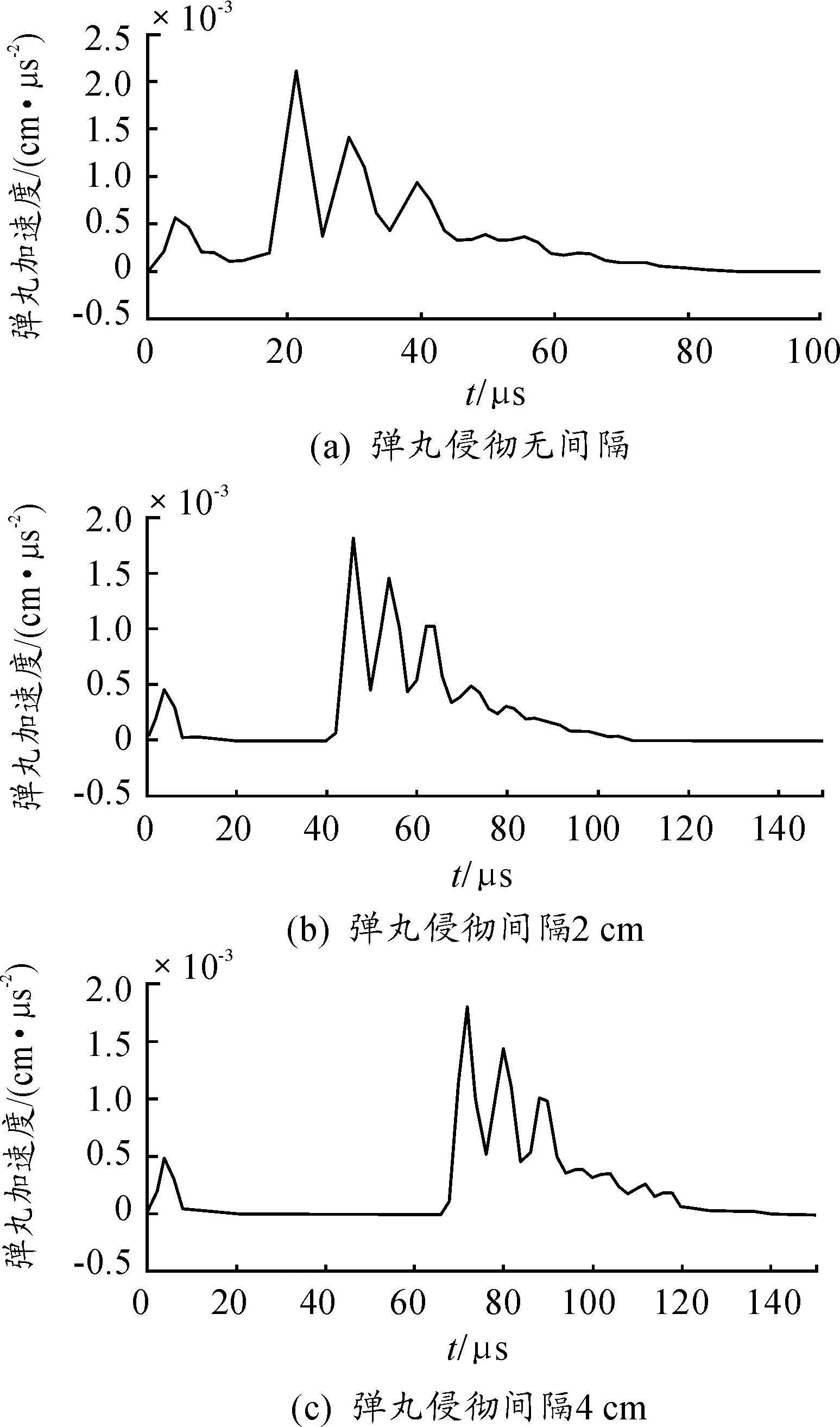
图3 三组侵彻仿真实验弹丸速度时程曲线

弹丸加速度变化反映了靶板的抗侵彻性能，加速度变化越大、越急剧，则靶板的抗侵彻性能越好。对比分析实验组和对照组的弹丸加速度变化可知，无间隔陶瓷/钢复合靶的钢背板对陶瓷靶板存在支撑作用，有间隔复合靶板的陶瓷靶板没有钢靶板的支撑保护，因而无间隔陶瓷/钢复合靶板的抗侵彻性能要优于有间隔陶瓷/钢复合靶板的抗侵彻性能。

2.3 弹丸变形

图4、图5、图6分别是实验组、对照组1、对照组2在弹丸击穿陶瓷靶板、钢靶板时刻的形态和基于剪切应变能的等效应力云图。图4(a)、图5(a)、图6(a)对应弹丸击穿陶瓷靶板时刻，此时实验组弹丸头部应力值最大、弹头形变最大；图4(b)、图5(b)、图6(b)对应弹丸击穿钢靶板时刻，此时实验组弹丸头部镦粗最严重。

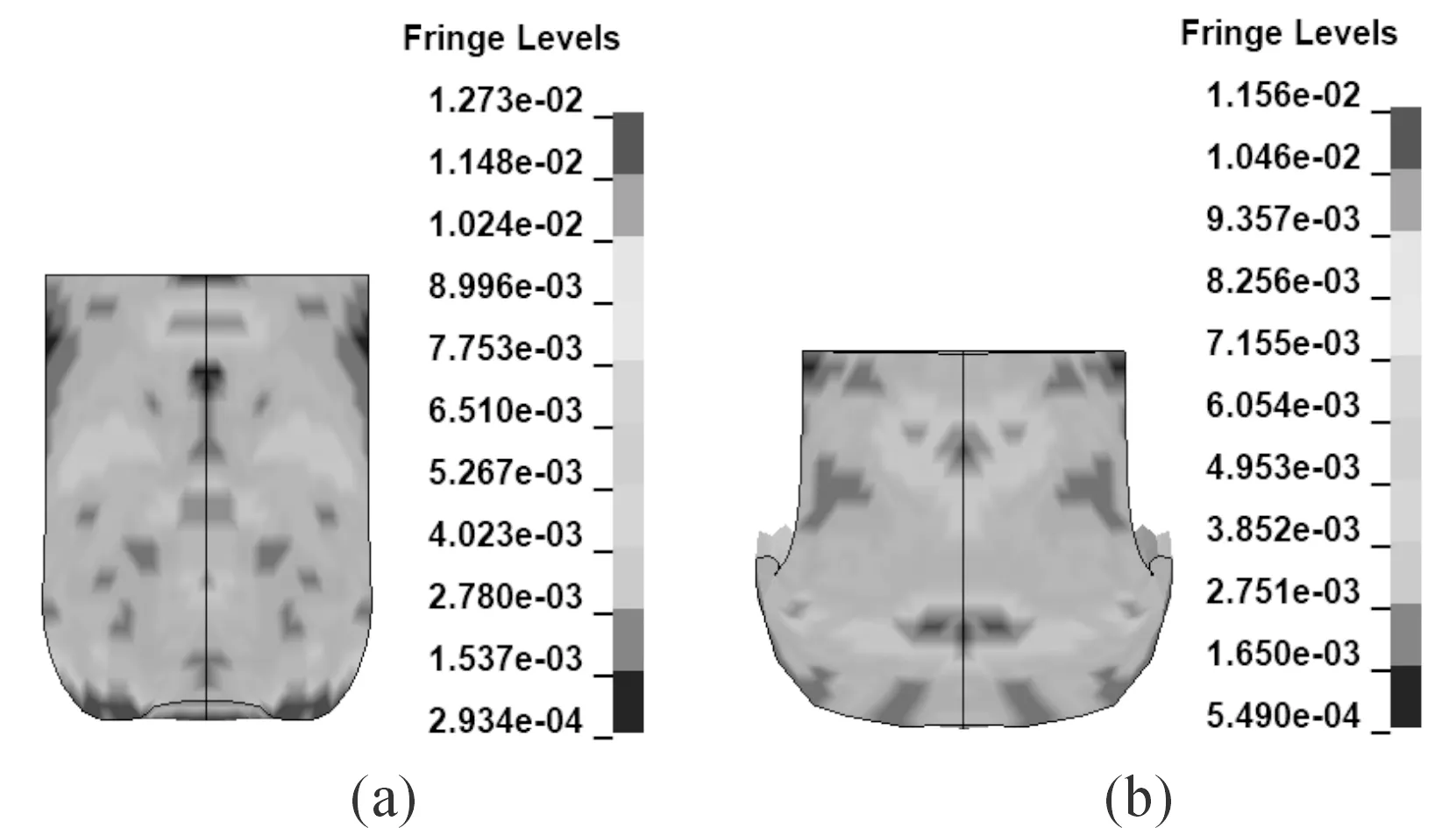
图4 实验组弹丸形态

图5 对照组1弹丸形态

图6 对照组2弹丸形态

表4是三个仿真实验中弹丸在初始时刻、击穿陶瓷靶板时刻、击穿钢靶板时刻轴向长度。

表4 弹丸轴向长度

通过对侵彻仿真实验中弹丸长度变化分析可知，实验组的弹丸长度在击穿陶瓷靶板时和击穿钢靶板时均最小，反映了无间隔陶瓷/钢复合靶板的抗侵彻性能要优于有间隔陶瓷/钢复合靶板。

2.4 靶板破坏

高速弹丸击穿陶瓷靶板后半球形头部被镦粗，之后对钢靶板的破坏机理由侵彻破坏变成冲塞破坏，弹丸击穿钢靶板后钢靶板背部隆起并形成冲塞破片。图7为三组侵彻仿真实验击穿钢靶板后靶板整体变形情况。

分析图7可知，在弹丸侵彻无间隔陶瓷/钢复合靶板仿真实验中，弹丸击穿钢靶板后，钢靶板被击穿区域挠度最大；在弹丸侵彻有间隔陶瓷/钢复合靶板仿真试验中，弹丸击穿钢靶板后，钢靶板的被击穿区域形变较小。钢靶板发生的形变越大，意味着钢靶板从弹丸吸收了更多的能量，则弹丸击穿复合靶板后的剩余速度就更小。因此，可以认为无间隔陶瓷/钢复合靶板具有更优越的抗侵彻性能。

图7 钢靶板被击穿后靶板整体受力云图

3 仿真模型理论分析

针对实际侵彻实验耗时耗力等问题，对某些物理条件进行假设，考虑主要因素对实际侵彻实验的影响，忽略次要因素对实际侵彻实验的影响，建立简化模型进行理论分析，在一定程度上可预测实际实验结果，计算模型结果一般能够满足工程设计要求。本文在第2部分中，通过弹丸侵彻陶瓷/钢复合靶板仿真实验得到弹丸的剩余速度，但缺乏理论分析计算的支持。理论验证以弹丸侵彻无间隔陶瓷/钢复合靶板仿真实验为主要分析对象：弹丸撞击陶瓷靶板，陶瓷破碎产生的碎片对弹丸的继续侵彻有阻力作用，钢背板对陶瓷靶板也有支撑作用；弹丸击穿钢靶板后在钢靶板上留下穿孔。根据能量守恒、动量守恒、质量守恒、材料本构模型，并假设在侵彻过程中弹丸质量不变，可以获得弹丸剩余速度与弹丸初始速度的关系，并以此为理论模型对侵彻仿真实验得到的弹丸剩余速度进行对比。弹丸剩余速度与弹丸初始速度的关系如式(1)所示[3],[16-17]：

式中：Vr是弹丸击穿无间隔陶瓷/钢复合靶板后的剩余速度;V0是弹丸初始速度；mp是弹丸质量；ρc为陶瓷靶板密度；Rc为陶瓷靶板的穿孔半径，仿真实验测得Rc=2.3 cm；hc为陶瓷靶板厚度；ρs为钢靶板密度；Rs为钢靶板的穿孔半径，仿真实验测得Rs=2.1 cm；hs为陶瓷靶板厚度；Rp为弹丸半径。弹丸以不同初始速度侵彻无间隔陶瓷/钢复合靶板，仿真实验得到的弹丸剩余速度Vsr和理论计算得到的弹丸剩余速度如表5所示。

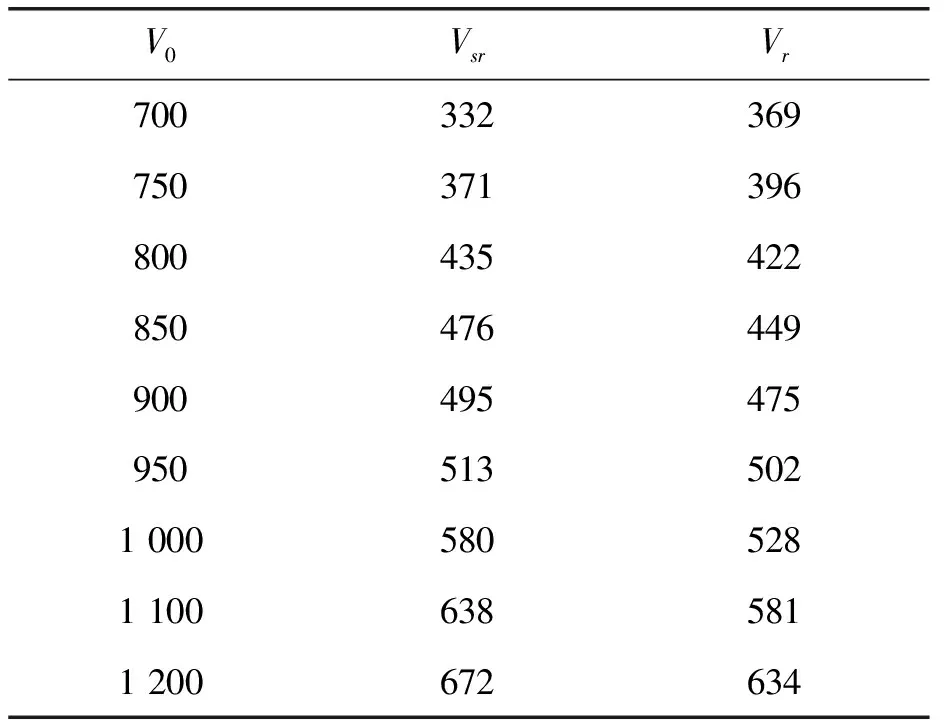
表5 侵彻仿真实验和理论计算得到的弹丸剩余速度 (m·s-1)

弹丸以不同初始速度侵彻无间隔陶瓷/钢复合靶板，仿真实验得到的弹丸剩余速度和理论计算得到的弹丸剩余速度如图8所示。

图8 仿真实验与理论计算得到的弹丸剩余速度

由图8可知，在不同弹丸初始速度条件下，侵彻仿真实验得到的弹丸剩余速度与理论计算得到的弹丸剩余速度在数值上吻合度较高，都是随弹丸初始速度的增大而近似线性增大，在一定程度上验证了仿真模型的准确性。

4 结论

1)在弹丸侵彻初期，弹丸撞击高脆性的陶瓷靶板，弹丸头部与陶瓷靶板接触面应力瞬间增大，弹头镦粗变平，增大了弹丸的侵彻阻力；

2)对比三组侵彻仿真实验，在弹丸侵彻无间隔陶瓷/钢复合靶板的实验组中，弹丸的加速度最大，剩余速度最小，钢靶板被击穿后弹丸形变最大，主要表现在弹丸轴向长度缩短最大、头部镦粗最大，钢靶板被击穿区域挠度最大；

3)在整个侵彻历程中，由于钢靶板对脆性较高的陶瓷靶板的支撑保护，使得无间隔陶瓷/钢复合靶板的抗侵彻性能要优于有间隔陶瓷/钢复合靶板的抗侵彻性能。