基于排队论的智能仓库机器人数量需求分析

闫 华，黎丽荣，万 飞，刘 波，李 睿

(1.陆军勤务学院，重庆 401311；2.军事交通学院 汽车士官学校，安徽 蚌埠 233011)

在智能仓库中，拣选作业主要采用“货到人”拣选方式，即由机器人将移动货架(托盘)搬运至拣选站台，然后由人工完成拣选作业[1]。这种拣选方式拣选效率高，能够有效节约人力，降低作业成本。但在电商物流中心的运营过程中，作业高峰期出现拣选效率低下并且拣选成本增加的现象，除了机器人路径规划方面的原因外，由于智能搬运机器人配置数量不科学，造成货架搬运不利、站台等待时间增加，导致拣选作业效率低下，也是其主要原因之一。

因此，需要对智能仓库中移动机器人的需求量进行分析，综合考虑订单数量、拣选效率以及成本等因素，建立机器人数量计算模型，通过求解得到合理的机器人数量，从而解决作业高峰期出现的拣选效率降低、成本增加等问题。

目前，对智能仓库中搬运机器人相关问题的研究，主要集中在搬运机器人设计与实现[2-3]，机器人多任务协作调度[4-5]，仓库布局优化[6-7]，以及机器人路径规划算法研究[8-9]等领域，针对智能仓库机器人数量计算的相关研究很少。实际应用中，大部分都是根据经费预算和机器人市场价格进行粗略估算。

本文首先对智能仓库机器人数量需求分析问题进行了描述，通过将订单和搬运机器人抽象为随机服务系统中的顾客和服务台，该问题可简化为多服务台排队问题；其次，从拣选成本角度出发，综合考虑时间成本、距离成本和设备成本，建立了机器人数量需求分析模型；再次，基于排队论基本理论，给出了智能仓库机器人数量分析过程中的主要指标及其计算公式；最后，通过Matlab建立仿真程序，对某智能仓库取不同数量机器人时的各项系统指标及目标函数进行了计算，并分析得到最优的机器人配置数量。

1 问题描述

智能仓库中一般采用“货到人”拣选方式，因此，搬运机器人的主要任务是根据系统分配的订单，将货物所在的移动货架运至拣选人员作业区域。如果将仓库中到达的订单看作顾客，那么一个搬运机器人就可看作一个服务台，则搬运机器人数量计算问题就可抽象为多通道等待排队问题，此处多通道为多个服务台，即智能仓库中的多个机器人。多通道排队问题，其特征与单通道标准模型特征完全相同。

在智能仓库中，由订单、机器人和拣选人员组成的拣选系统如图1所示。

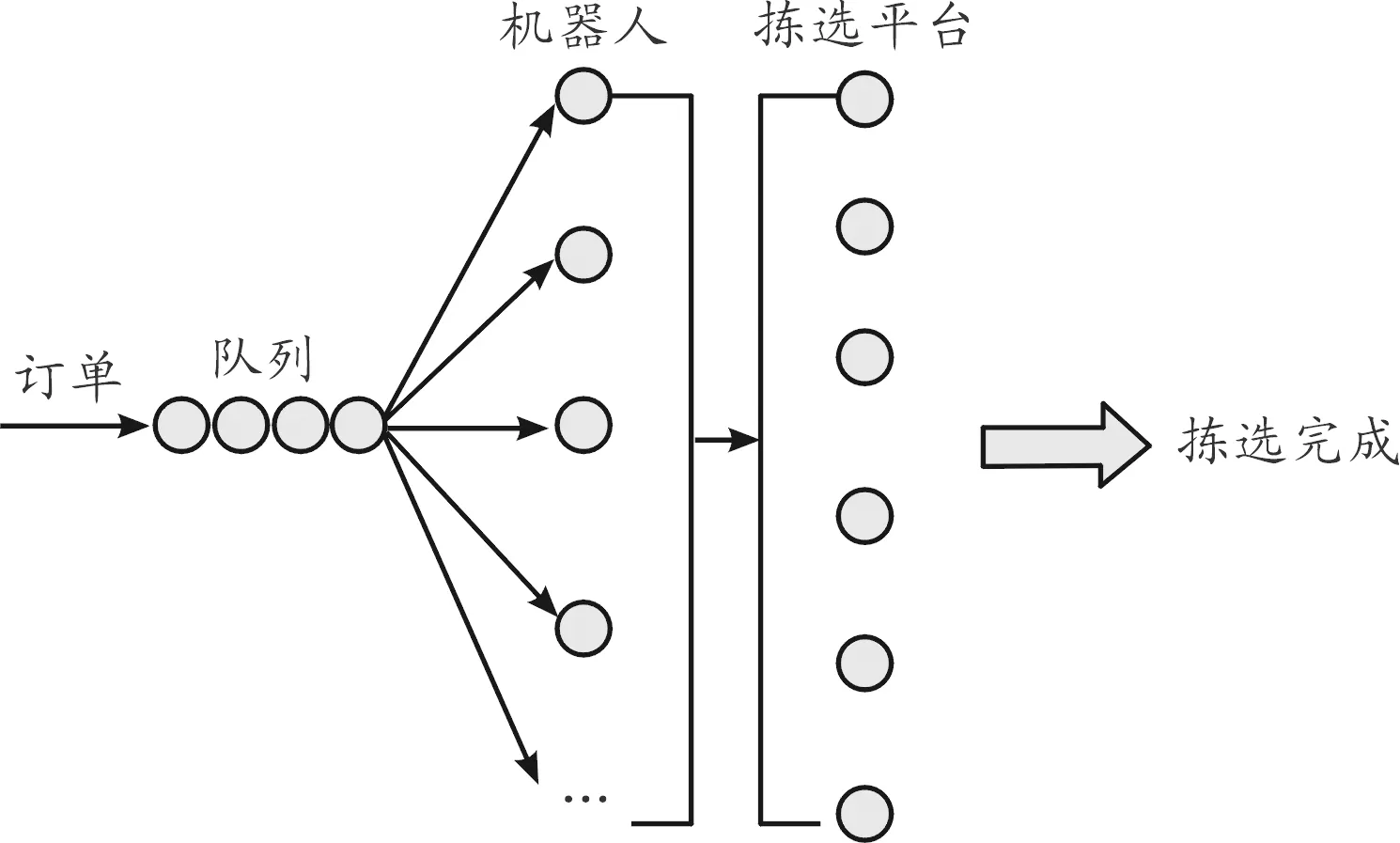
图1 机器人数量需求分析系统示意图

智能仓库机器人数量需求分析问题主要研究不同数量的搬运机器人对订单的服务情况，问题目标可表述为在满足订单拣选需求的前提下，尽量减少系统中订单的等待时间(或系统中等待拣选的订单队长)，同时尽量提高机器人利用率，避免资源闲置，达到较高的投资效益。因此，在研究过程中，假设人工拣选平台总能满足拣选需求，只考虑机器人服务订单的情况。此时，可将仓库机器人数量需求问题抽象为一个多服务台排队问题，即单队、并列的多服务台(M/M/C)排队模型。

2 智能仓库机器人数量需求分析模型

从拣选成本角度建立智能搬运机器人需求数量计算模型的目标函数。拣选作业成本通常包括时间成本、距离成本和设备成本。

1)时间成本。仓库中的拣选活动根据订单货物的不同，其拣选时间长短不同。拣选时间越长，则拣选作业的时间成本越高；反之，则时间成本越低。

2)距离成本。待拣选商品与仓库理货区的距离，也是拣选作业成本应考虑的因素。距离越远，则拣选作业时间及能量消耗越大，拣选作业成本越高。

3)设备成本。拣选作业时，拣选设备利用率的高低会影响作业成本。若设备闲置空转，利用率低，会造成资源浪费，显然会增加拣选作业成本。因此，在计算拣选作业成本时，应考虑拣选设备的利用率。

令tN表示系统中有N个搬运机器人时订单的平均服务时间，服务时间越长，则时间成本越高。取tmin为系统的最小服务时间。令ts=tN/tmin，则ts表示当前系统的平均服务时间与系统最小服务时间之比，ts越大，表明每个订单平均服务时间越长，即时间成本越高。

由于智能搬运机器人数量的多少并不影响批次订单的拣选距离，且虽然对多智能搬运机器人行走路径进行了优化，但由于在仿真系统中，无法获取规划前后机器人拣选路径优化程度的具体量化数值，因此，这里假设机器人数量的变化，不会对拣选距离产生影响。

设备成本在此处具体体现为系统的拣选效率，可以系统中每个机器人的平均空闲率P0=1-r作为衡量指标。r代表单个机器人工作概率，P0反映了系统中每个机器人的空闲程度，该值越大，表明智能搬运机器人的利用程度越低，则拣选成本越高。

综上所述，可建立智能搬运机器人需求数量分析模型的目标函数如下：

minF=ts+P0

(1)

假设订单的到达服从泊松分布，则可基于多服务台排队系统理论，通过分析，计算得到当系统取不同智能搬运机器人数量N的情况下，系统的拣选作业成本F，则当F最小时，即为最优的机器人数量。

3 基于排队论的机器人数量计算

假定仓库中到达的订单服从泊松分布，其到达率为λ；仓库中有C个机器人，每个机器人相互独立工作，且每个机器人的服务率μ均相同，则整个仓库对订单的平均服务率为Cμ。令ρ=λ/Cμ为系统的服务强度或服务机构的平均利用率，显然只有当ρ<1时才不会排成无限长的队列，下面列出相关符号定义。

λ为订单到达率，μ为单个机器人的服务率，C为机器人数量，ρ为系统服务强度，Ls为平均订单数，Lq为平均等待的订单数，Ws为订单平均逗留时间，Wq为订单平均排队等待时间。

记Pn为系统中有n个订单的概率，根据排队论相关理论可得：

(2)

(3)

系统的运行指标计算公式如下：

(4)

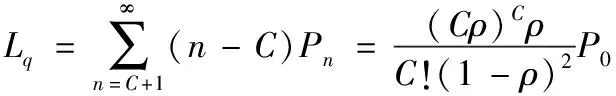
(5)

(6)

(7)

在进行智能仓库机器人数量分析过程中，主要对以上指标进行分析：平均队长Ls，指系统中的平均订单数量，包括等待和正在拣选的订单数量总和；平均排队长Lq，指系统中等待拣选的订单数量；平均逗留时间Ws，指订单从到达系统到拣选完成的平均时间；平均等待时间Wq，指订单从到达系统到被拣选为止的平均时间。

4 算例分析

在仿真实验中，假定每小时平均到达的订单数为625个，单个搬运机器人每小时能够拣选完成的订单数量为20个，即λ=0.001 6，μ=0.05。同时，在仿真实验中做出以下假设：每个订单只有一种类型的商品；每种商品在一个货架的拣选能够一次满足。即每个订单的拣选任务能够由一个搬运机器人通过搬运一次移动货架完成。

基于上文建立的智能仓库机器人数量需求分析模型，通过Matlab建立仿真程序，并采用排队论理论进行计算，可得在不同机器人数量下的目标函数及系统中各项指标如表1所示。

从表1可以看出：根据提出的仓库机器人数量需求分析模型，当订单到达率λ=0.001 6，机器人服务率μ=0.05时，机器人数量C=35的目标函数值F=1.12，为最小值。此时，订单在系统中的平均服务时间为3.33，即单个搬运机器人每小时拣选完成的平均订单数量约为18个；同时，每个机器人的空闲率约为1%，基本上达到了对机器人的最大利用。

下面分别取机器人数量为32和40进行对比。当机器人数量为32时，由表1可以看出，系统中订单的平均服务时间为6.40，即单个搬运机器人每小时拣选完成的平均订单数量约为9个，此时，即使所有机器人都满负荷运转，也根本无法满足每小时平均625个订单的拣选要求；当机器人数量为40时，由表1可知：系统中订单的平均服务时间为3.03，即单个搬运机器人每小时拣选完成的平均订单数量约为20个，此时，若所有机器人全部工作，每小时可完成的订单数为800个，大于每小时需要处理的平均订单数量，因此，约有21%的机器人处于空闲状态。考虑机器人昂贵的购置成本，这一方案虽然满足了拣选数量要求，但是资金投入过高，且造成了一定程度的资源浪费。综上所述，从拣选效率、拣选成本综合分析可知，当λ=0.001 6，μ=0.05时，最优机器人配置数量为35台。

5 结论

通过综合考虑订单数量、拣选效率以及机器人购置成本等因素，建立了智能仓库机器人数量需求分析模型。基于排队论理论对系统的平均队长Ls、订单的平均逗留时间Ws等指标进行分析，并计算模型目标函数，可得考虑拣选效率和拣选成本等因素下的最优机器人数量配置。既能满足智能仓库中对订单的拣选需求，避免因为等待时间过长而造成的成本增加；同时，保证每台机器人都能够得到充分利用，避免机器人闲置导致投入过高和资源浪费。