基于全局局部一致性的多特征融合目标跟踪

徐 艳,王培光,杨 宁

(1.河北大学，河北 保定 071002；2.陆军工程大学石家庄校区，石家庄 050003；3.80集团军防空80旅，济南 250300)

在实际的运动目标跟踪过程中，目标位置和姿态的变换、目标尺度的变化、场景中光线变化、目标的快速运动、物体遮挡等，都会对目标跟踪的鲁棒性产生很大影响[1]。生成式目标跟踪方法通过对目标建立外观模型来预测目标的位置，在当前的硬件条件下更适用于在线目标跟踪。Kalman滤波方法对目标模型和噪声特性要求较高[2-3]，粒子滤波(PF)[4-5]和均值漂移[6-8]能够有效应用于非线性、非高斯的运动系统，具有较好跟踪效果。粒子滤波在传统算法的基础上衍生了多区域采样[9]、改进的重要性函数、自适应重采样算法[10]等新方法，但是当场景中有多个相似目标或目标与背景相似时，随机采样的误差累积会导致滤波器发散，进而造成滤波结果错误。Meanshift算法计算速度快，Vojir等[11]提出的RSAM(RobustScale-AdaptiveMean-ShiftforTracking)算法，是VOT2015官方推荐的一种基于颜色特征的实时算法，但当背景色和目标颜色接近时，有可能导致目标跟踪丢失。

为了解决遮挡、相似目标干扰等造成的目标丢失问题，李冠彬[12]、张彦超[13]等将目标区域划分成多个子区域，有效规避遮挡下的目标丢失问题，并综合多个分块跟踪结果确定最终跟踪位置；别秀德[14]、宋丹[15]等利用融合多种特征实现目标跟踪，增加图像的局部不变性，提高算法的鲁棒性；文献[16]使用meanshift算法对粒子进行聚类分析，但核函数宽度固定不变，导致目标大小发生变化或严重遮挡时，易产生跟踪滞后或丢失目标的现象。

本文利用粒子滤波实现全局基于DPM特征外观模型的滤波，提取重采样后的粒子群，基于HSV+LBP的融合特征，进行meanshift聚类处理，实现多特征下的局部外观模型的二次定位，并构建全局局部一致性条件下的跟踪结果融合策略，以得到目标的稳定、准确的跟踪位置。

1 全局局部一致性下的目标跟踪

1.1 基于DPM特征的全局粒子滤波

预测步骤为：

(1)

更新步骤为：

(2)

进而得到最小方差意义上的最优估计结果为：

(3)

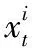
(4)

为了提高目标预测跟踪精度，本文首先采用DPM(Deformable Part Model)特征，建立梯度方向直方图作为全局特征；为了适应跟踪目标在尺度、角度旋转方面的变化，提高跟踪稳定性，将传统粒子滤波的矩形区域改为具有长轴、短轴和倾斜角参数的椭圆区域的特征模型来描述目标，从而完成基于DPM特征的全局粒子滤波过程。

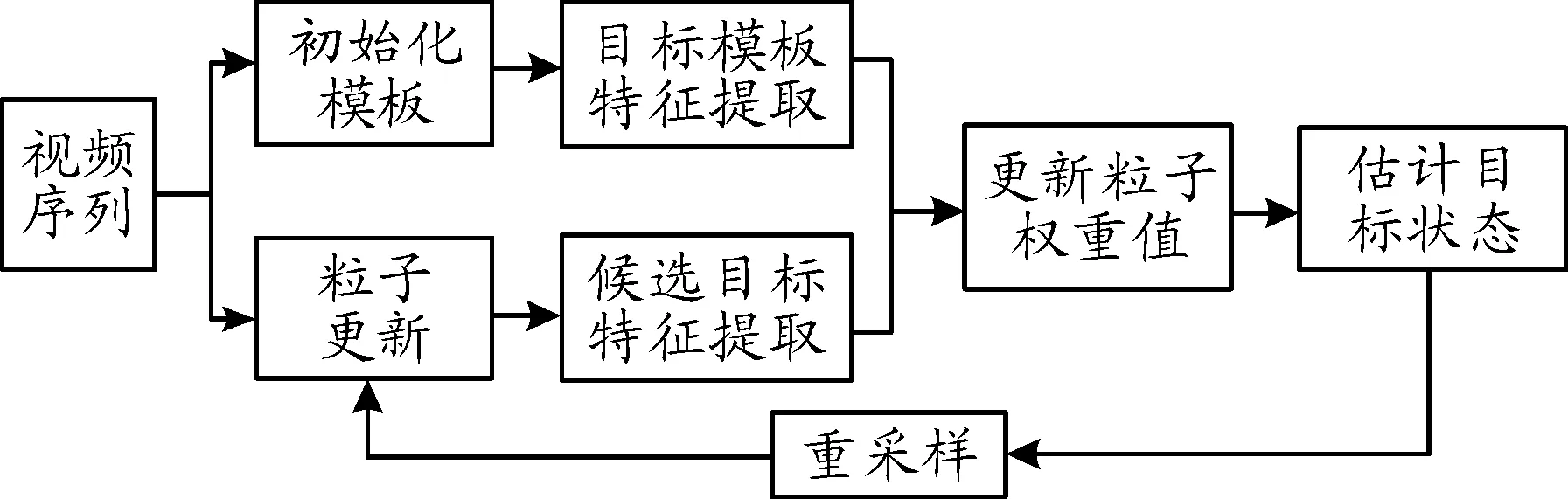
图1 粒子滤波目标跟踪流程图

为了提取DPM特征，本文采用4个8×8的Cell组成2×2的block，进而生成13维特征向量作为粒子的特征向量，并构建特征向量直方图，该直方图比传统基于颜色的8×8×8的直方图的特征向量维数要低11维，但是该描述子保持了几何和光学变化不变性，使得跟踪过程对于光照或阴影遮挡的抑制效果更好。

1.2 基于LBP+HSV的meanshift多特征局部滤波

为了解决粒子滤波中相似目标和背景对跟踪性能的影响，本文对重采样后的粒子群进行聚类处理，实现多局部区域的目标跟踪。

为了获取有效的局部区域的中心，本文通过meanshift对重采样的粒子集合进行非参聚类[17]以实现局部最大点的求取和区域最优估计。

本文提出LBP(Local Binary Pattern)+HSV的特征选择策略，首先在3×3窗口内得到8bit图像的局部纹理特征，在结合窗口中心像素的4×4×4的HSV颜色特征，组合得到20bit的融合特征向量，求取联合LBP和HSV特征直方图，得到局部区域的联合直方图。

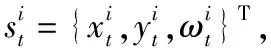
(5)

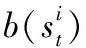
对于任一粒子s1处的概率分布可表示为：

(6)

取两点之间的巴氏距离作为相似度指标，有：

(7)

在粒子s0周围搜寻最优目标位置s1，两点的meanshift向量可表示为：

(8)

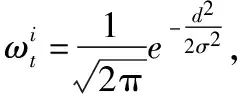
(9)

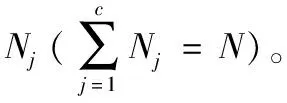
由于这个多维向量是局部区域的特征集合，虽然维数较多，但受到区域的限制，整体运算量的增加是有限的，表1列出了四种特征在指定局部区域大小(26×17)下meanshift运算时间，表1中四种算法均由matlab实现，硬件配置为intelxeonCPUE5-2630，内存为64G。由表1中数据可见，LBP+HSV的meanshift算法可以57fps的速度达到实时处理的效果。

表1 不同特征下的meanshift运算时间

1.3 全局局部一致性下的二次目标定位策略

由于Meanshift是一种统计迭代算法，通过迭代可以快速寻找概率密度估计的局部最大值，属于确定性跟踪算法，方法简单、收敛快，但跟踪过程中容易陷入局部最优状态，收敛于非真实目标。而粒子滤波算法属于随机性跟踪算法，适用于非线性非高斯状态下的目标跟踪，具有很好的稳定性以及抗遮挡性能，因此二者结合能够获得较好的跟踪效果。

根据局部meanshift区域中心像素位置，以及全局粒子滤波的中心位置，融合得到全局局部一致性下的目标位置，即：

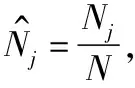
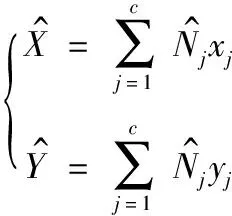
(10)

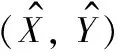
(11)

进而得到归一化后的粒子权值为：

(12)

全局局部一致性目标跟踪流程如图2所示。

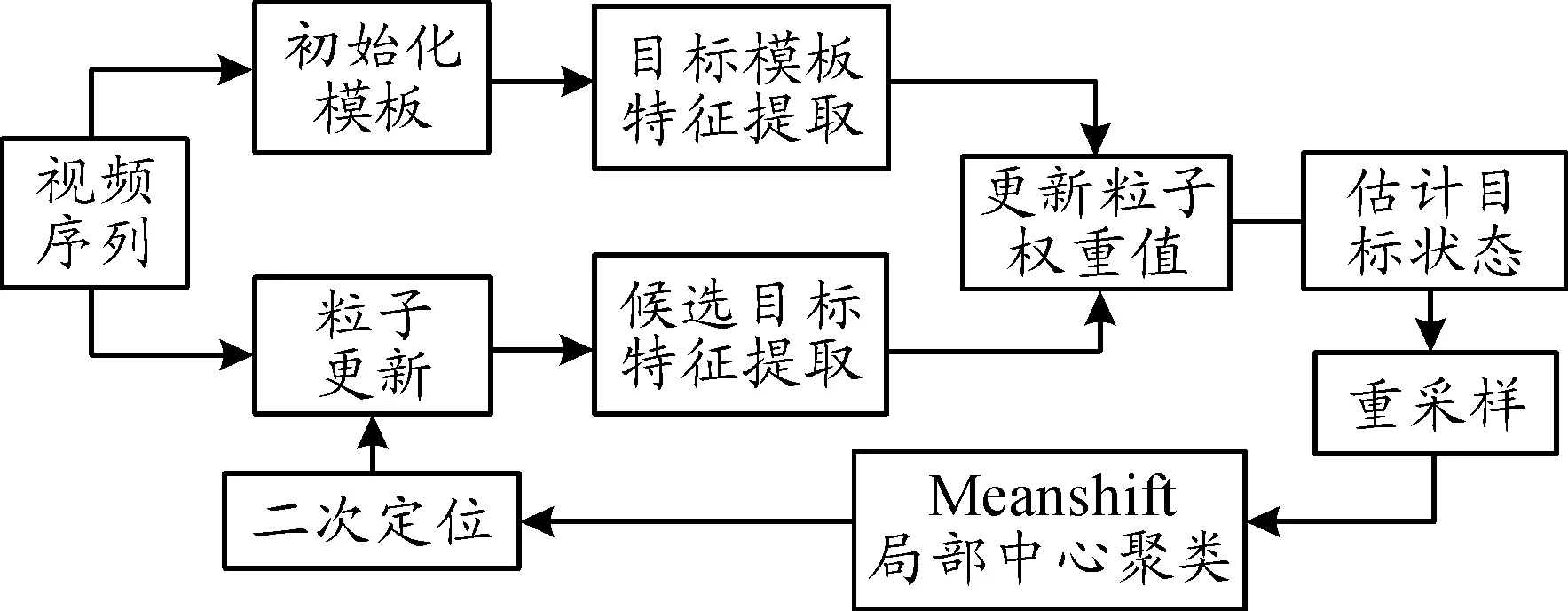
图2 全局局部一致性目标跟踪流程框图

综上，第t帧图像序列，其全局局部一致性下的目标定位步骤为：

步骤1全局DPM特征下的全局粒子滤波，式(1)—式(4)；

步骤2粒子重采样；

步骤3计算粒子的LBP+HSV特征直方图，得到32维特征向量；

步骤4基于meanshift的粒子局部极值点计算，公式(9)；

步骤5全局局部一致性下的二次目标定位，粒子及权值更新，式(10)—式(12)。

2 实验

为验证试验效果，在Intel Xeon(R)CPU E5-2630，64G内存，NVIDIA GTX 1080 Ti的平台上，利用Matlab软件运行算法。选取OTB100数据集进行实验，将本文算法与基于分块的粒子滤波[14]、PF+meanshift算法[17]进行对比分析。

为了验证本文算法的跟踪精度，分别提取稳定跟踪阶段的跟踪误差并计算算法的平均定位精度，见表2。图3为跟踪精度变化曲线。

表2 算法的定位精度

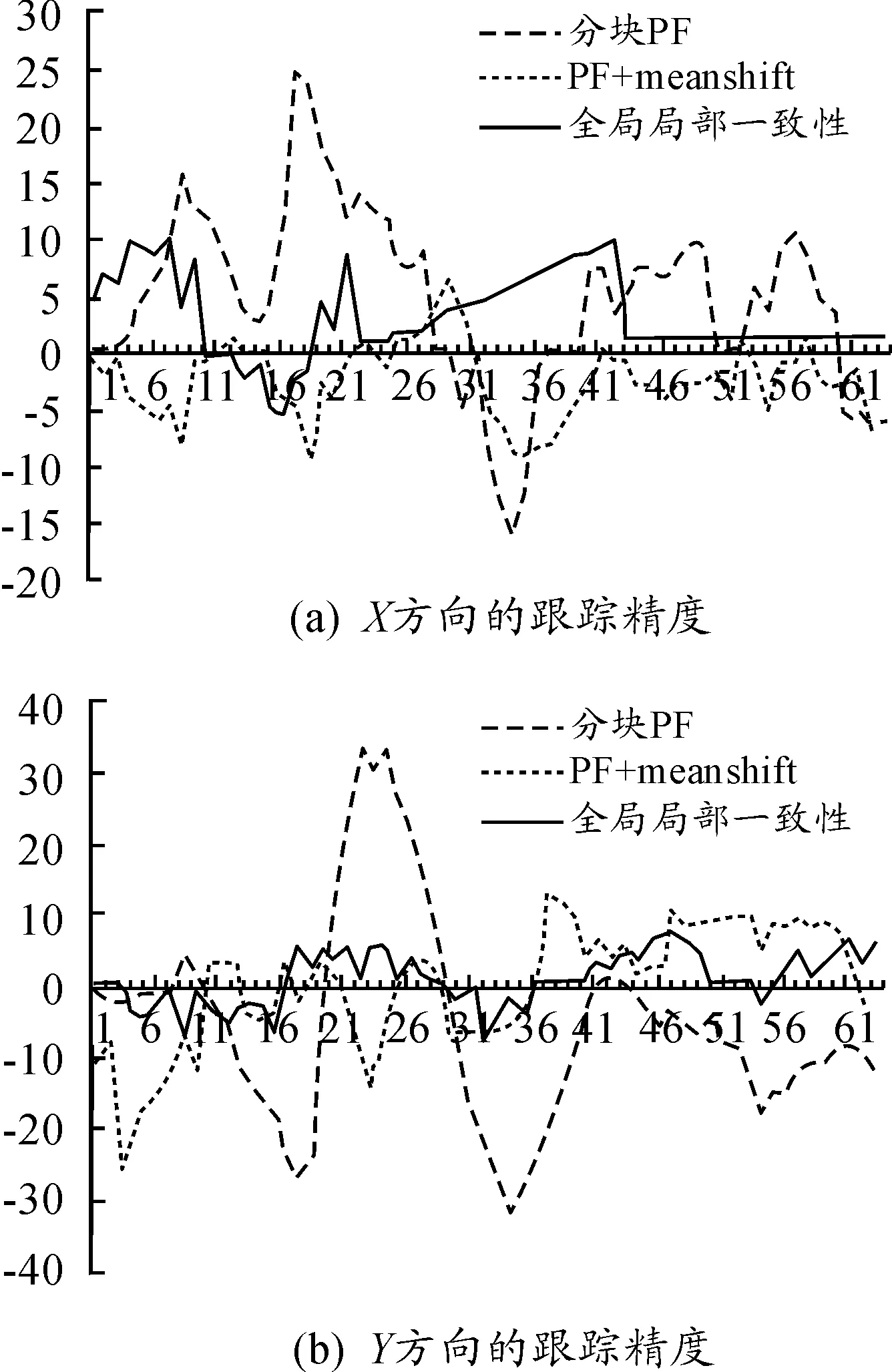
图3 跟踪精度变化曲线

文献[17]的算法对于红外目标取得了较好的效果，但是由于原始算法采用了灰度信息作为特征，在很大程度上制约了其跟踪效果的提升，在实验过程中，采用DPM代替原有灰度特征，平均定位精度最小可以锁定到2个像素内，而在本文算法中，将全局局部特征融合，二次定位的精度可达1个像素内，可见定位精度有明显提升。

在整个实验过程中，背景环境较为复杂，跟踪目标会出现遮挡和快速移动的情况。如图4所示，目标在被遮挡时，分块粒子滤波仍然能够跟踪目标，但会出现跟踪误差较大的情况，在第489帧，目标出现快速移动时，跟踪失败，并且无法找回目标。

对于PF+meanshift算法，在目标区域已知的情况下完全可以做到实时跟踪，对遮挡、目标变形等不敏感。当目标受到遮挡时，PF+Meanshift依然能够稳定跟踪，但跟踪精度相比本文算法稍低，且当目标快速运动时，由于算法是在PF基础上的跟踪，因此仍然会丢失目标。

图5为本文算法的跟踪效果。当目标出现快速移动时，Meanshift两个局部滤波结果依然能够稳定跟踪，算法整体没有失效，并可计算出目标二次定位位置。

图4 分块粒子滤波遮挡和快速移动

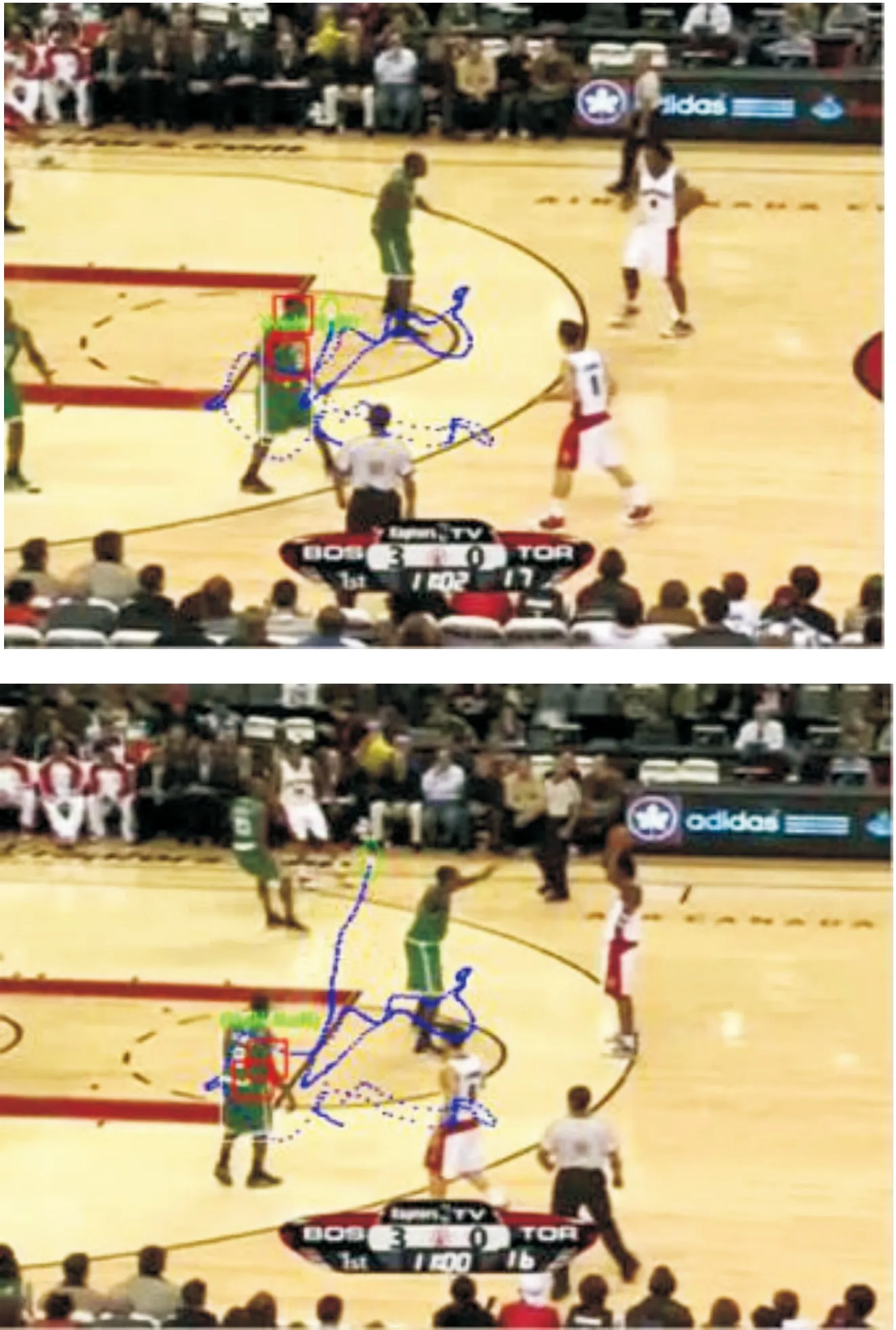
图5 目标快速移动时本文算法跟踪结果

3 结论

本文基于DPM特征构建归一化直方图，完成全局粒子滤波，找到目标一次定位结果；在重采样后提取粒子群的LBP+HSV的融合特征，在融合特征直方图的基础上实现对粒子群的局部极大值聚类，构建全局局部一致性条件下的二次目标定位策略，利用二次定位结果更新全局粒子及其权值。本文算法将鲁棒性较强的全局颜色信息与局部纹理信息相结合，构建权重可调的全局局部一致性状态估计模型，从而得到目标当前状态。实验结果表明：该算法能够较好地处理目标跟踪常见的遮挡、干扰、目标快速移动等情况，定位精度和稳定性得到改善。