导弹定期维修条件下的贮存可靠性预测方法
蒋 平,邢云燕,王 博,齐建军
导弹定期维修条件下的贮存可靠性预测方法
蒋 平1,邢云燕1,王 博1,齐建军2
(1. 国防科技大学系统工程学院,长沙,410073;2. 北京特种工程设计研究院,北京,100028)
导弹在寿命周期大部分时间处于贮存中,且在长贮过程中会进行定期检测维修。考虑到维修可能对导弹贮存可靠性的影响,论文基于导弹贮存寿命服从威布尔分布的假设,考虑存在初始失效的导弹定期维修的背景下,对最常见的修复如新、贮存失效率增大的情况,提出了贮存可靠性预测模型,并用最小二乘估计对维修后的模型参数进行了估计。最后,通过文献中的数据验证了所提的贮存可靠性预测模型,结果表明模型能较好地预测导弹贮存可靠性在定期维修条件下的变化规律。
导弹;定期维修;威布尔分布;贮存可靠性预计
0 引 言
导弹等装备在其寿命周期中大部分时间都处于贮存或非工作状态,统称为长贮装备。为了保证长贮装备结束贮存、投入使用时具备很高的可靠性,贮存可靠性要求极高。贮存可靠性的定义是:在规定的贮存条件下,在规定的时期内,贮存后,产品满足规定功能的能力。长贮装备在经过一段时间的贮存后,由于在贮存期间受到自然因素(温度、湿度、大气压力、霉菌、盐雾等)和诱导因素(电磁辐射、静电、振动、冲击等)的影响,造成各部件性能参数的退化或者突发故障的发生,导致贮存可靠性下降。为使长贮装备保持较高的可靠性和战备完好率,在贮存期间必须进行检测和维修(包括检测、修理和更换)。大多数产品在贮存期间经过维修后,贮存可靠性和失效率都会受到影响。因此,通过分析维修对长贮装备贮存可靠性的影响,选择适当的数学模型来描述贮存可靠性的变化规律,并通过正确的方法来求解模型中的参数,才能对长贮装备的贮存可靠性做出准确预测。
现有文献在考虑产品贮存过程中的维修对产品可靠性的影响时,主要针对维修前后可靠性参数(如失效率)的变化规律开展研究。产品在贮存期间经过维修后,可靠性往往难以恢复到初始状态,失效率也因为维修类型的不同而存在差异。张永进和赵明[1]将维修对失效率的影响类型总结为3种模型:a)修复如新,维修后失效率增大;b)修复不如新,维修后失效率不变;c)修复不如新,维修后失效率增大,并根据这 3种模型维修前后的可靠性变化提出了产品贮存寿命参数的Bayes估计,将其应用于指数分布产品贮存期间的贮存寿命评定。
在装备的长贮过程中,维修方式可分为定期维修、收发维修和视情维修。由于定期维修便于组织管理,已成为工程实践中最常用的维修方式。因此,徐廷学[2]对定期维修方式提出了2类模型:a)对系统的整体维修,维修发现故障后修复,修复后可靠度虽然与修复前一样,但失效率大于修复前;b)对部分设备的维修修复,由于导弹的更换件和不更换部分的相互影响,将引起维修后系统可靠度的下降,利用两类模型的失效率与维修周期的关系,通过残存比例法估计维修后的系统可靠性。张金春和刘超[3]考虑到定期维修中电源通断循环等因素对导弹武器系统的影响,提出了测试效率对系统失效率的影响问题,建立了定期维修对导弹系统贮存可靠性影响的数学模型。
维修的根本目的是为了保证产品满足给定的可靠性要求,因此大量文献对维修的策略开展研究,主要是根据可靠性指标要求或寿命周期费用约束来确定最优的维修周期或维修策略。例如,李大伟等[4]通过分析维修对产品技术状态和失效变化规律的影响,利用复合泊松过程来描述维修效果,得到了定期维修条件下产品寿命分布变化规律。在此基础上,提出了一种定期维修与视情维修相结合的混合维修策略,通过费用优化,给出了最优的定期维护周期和预防性维修阈值。在定期维修的前提下,Ito等[5]根据事先确定的维修对失效率的不同影响,考虑维修费用、故障损失和更换费用,以单位贮存时间平均费用最低为目标,确定最优维修周期和贮存时间。李青和荣军[6]通过引入测试效率来表示每次维修后系统可靠性的变化,同样考虑了维修、更新系统的费用和系统的故障损失3类费用,结合可靠性模型来建立费用约束的非线性规划模型,以费用最小化为目标来求得最优维修周期。当维修对失效率的影响难以确定时,Kallen和Noortwijk[7]使用Markov过程来描述系统性能参数的退化,确定最优的维修周期使寿命周期单位时间的平均费用最低。王小林等[8]考虑了性能退化产品在受到冲击影响下的不完全维修策略。Huynh等[9]在考虑性能退化失效与冲击失效竞争引起产品失效的情况下,提出了以寿命周期平均费用最小作为目标的定期维修更换的维修决策方法。王永攀等[1,10]研究了定期维修条件下维修备件和故障件维修工人的维修资源配置问题,建立了系统的平均备件短缺概率模型。张耀辉等[1,11]提出了基于关键零部件技术状态信息优化定时维修间隔期的方法。
在建立可靠性的模型后,进一步需要估计参数估计,才能预测可靠度。罗吉庭等[1,12]假定导弹贮存可靠性的变化规律呈现指数衰减的情况下,根据各维修时刻的试验数据来确定模型参数。此外,在导弹研制和使用过程中存在贮存可靠性相关的历史信息。在很多场合,工程专家可以根据自己的经验对产品的贮存可靠性给出自己的判断。刘飞等[13]针对这类信息提出了一种导弹贮存可靠性预测的贝叶斯模型,该模型在Mazzuchi-Soyer可靠性增长模型的基础上,利用历史信息和专家判断,结合导弹各维修时刻的成败型试验数据,给出各维修时刻可靠度的联合后验分布,然后利用Gibbs抽样进行后验推断,得到各阶段可靠性的贝叶斯估计,预测导弹的贮存可靠性。吴和成等[14]基于检测的成败型数据,给出了一种确定指数型元件的贮存可靠性置信下限的方法。李彦彬等[15]研究了导弹的定期检修问题,对导弹部件检修方式进行了分类,进一步建立了导弹的贮存可靠性模型,并运用极大似然估计和牛顿迭代法来估计参数。
现有文献考虑维修对贮存可靠性的影响时,较少考虑寿命服从威布尔分布的产品,而且对影响的分类讨论和模型参数求解也不完善。因此,本文针对贮存寿命服从威布尔分布的长贮装备,根据最常见的修复如新、故障率增加的情景,建立了贮存可靠性的预测模型,并给出了参数的求解方法。
1 考虑定期维修的贮存可靠性模型
1.1 基本假设
威布尔分布对各种类型的试验数据具有极强的适应能力,在可靠性工程中扮演了重要角色[16]。因此,本文假设导弹的贮存寿命服从威布尔分布。对定期维修的假设条件如下:
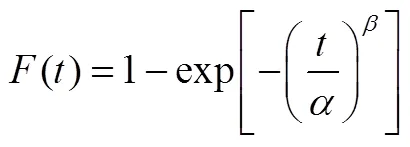



1.2 贮存可靠性预测模型
本文在张永进等[1]提出的3类具有初始失效的导弹定期维修贮存可靠性模型的基础上,选择了第1类,即修复如新、失效率增加的情景,研究了贮存寿命服从威布尔寿命分布的贮存可靠性预测。
为准确描述该模型,提出如下假设:
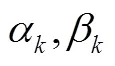


第次维修后的失效率为
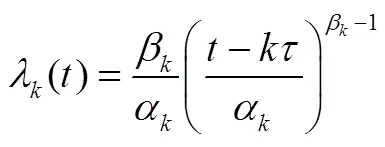


图1 修复如新、失效率增大时的贮存可靠性变化趋势示意

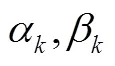

由于时刻的贮存可靠性为

将威布尔分布的失效率函数代入式(10)得
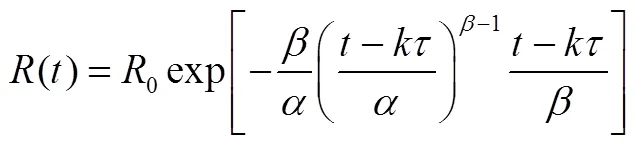
即:
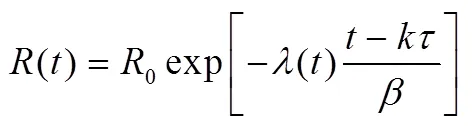
将各维修期内的失效率公式(7)代入式(12),得:

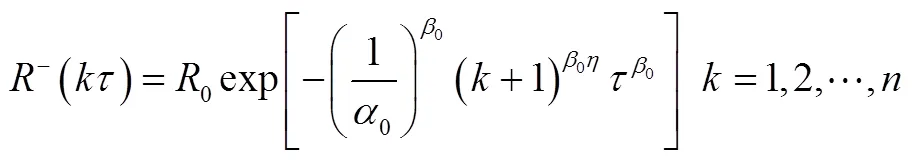
1.3 模型参数估计
在使用贮存可靠性模型进行可靠性预测前,首先需要确定模型的参数。威布尔模型参数较多,函数形式比较复杂,参数估计过程比指数分布和正态分布的参数估计困难。借鉴张永进等[1]的研究成果,在此基础上推导出了贮存寿命服从威布尔分布的模型参数。
1.3.1 维修前可靠度的贝叶斯估计


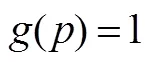

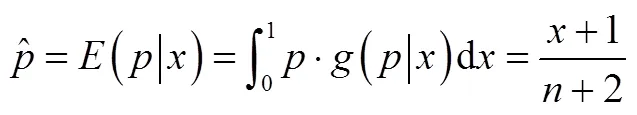

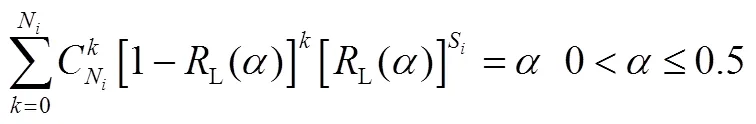
下面给出模型中其他参数的最小二乘估计。
1.3.2 参数的最小二乘估计
将贮存可靠性式(13)两边取对数,进行线性化,得:



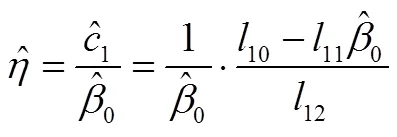
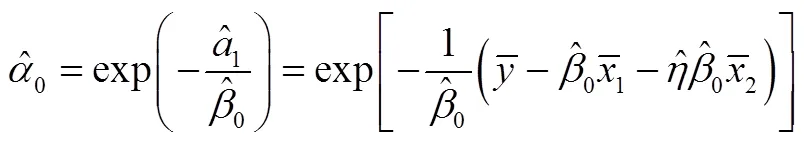
2 案例分析
2.1 成败型数据

表1 100个产品的定期维修数据
Tab.1 Periodic Maintenance Data for 100 Products
可靠度极大似然估计可靠度贝叶斯估计 010011(99,100,0)0.99000.9804 19945(95,99,1)0.95960.9505 295510(90,95,2)0.94740.9479 390313(87,90,3)0.96670.9565 487720(80,87,4)0.91950.9101 580525(75,80,5)0.93750.9268 675833(67,75,6)0.89330.8831 767740(60,67,7)0.89550.8841 860444(56,60,8)0.93330.9194 956650(50,56,9)0.89290.8793 10501161(39,50,10)0.78000.7692

由表1数据可知,该产品的初始可靠度极大似然估计为0.99,而贝叶斯估计为0.9804,根据式(15),确定该产品的初始可靠度为0.98。
通过Matlab模拟可以计算出模型的可靠度估计值,并得到与可靠度点估计的绝对误差,如表2所示。同时,可以得到相应的参数值:


表2 推移时间后的产品定期维修数据及可靠度估计
Tab.2 Time Delayed Periodic Maintenance Data and Reliability Estimation
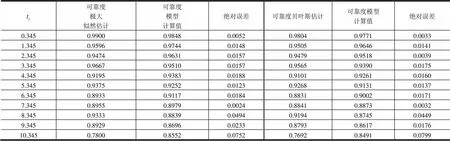
可靠度极大似然估计可靠度模型计算值绝对误差可靠度贝叶斯估计可靠度模型计算值绝对误差 0.3450.99000.98480.00520.98040.97710.0033 1.3450.95960.97440.01480.95050.96460.0141 2.3450.94740.96310.01570.94790.95180.0039 3.3450.96670.95100.01570.95650.93900.0175 4.3450.91950.93830.01880.91010.92610.0160 5.3450.93750.92520.01230.92680.91310.0137 6.3450.89330.91170.01840.88310.90020.0171 7.3450.89550.89790.00240.88410.88730.0032 8.3450.93330.88390.04940.91940.87450.0449 9.3450.89290.86960.02330.87930.86170.0176 10.3450.78000.85520.07520.76920.84910.0799

图3 贝叶斯估计值和模型计算值拟合
2.2 寿命型数据


表3 残存比率法的可靠度点估计
Tab.3 Reliability Point Estimation by Survival Ratio Method
故障时间t/年0.0830.1650.3340.4150.4170.8330.9551.3341.920 可靠度点估计0.88040.86080.84130.82170.80210.78260.76300.74350.7239 模型计算可靠度0.87960.86280.84150.82090.80140.78520.76000.74590.7210 绝对误差0.00080.00200.00020.00080.00070.00260.00300.00240.0029
根据预测方程对第3年的第1次维修结果进行预测,比较结果如表4所示。
表4 预测结果
Tab.4 Estimation Results
故障时间t/年可靠度点估计预测可靠度预测值的绝对误差 2.0830.70440.73820.0338
图4为残存比例法估计和模型计算值拟合。

图4 残存比例法估计和模型计算值拟合
3 结 论
以长贮装备的典型代表导弹为研究对象,基于威布尔分布建立了修复如新、故障率增加情景下的贮存可靠性预测模型,给出了模型的参数估计方法。通过实例分析,提出的定期维修条件下的长贮装备贮存可靠性预测模型能较好地反映贮存可靠性的变化规律,可为确定长贮装备的维修策略和维修时机提供技术支持。
所建立的基于威布尔分布的考虑维修的贮存可靠性模型虽然形式较复杂,但在工程实际情况下,通过选择适当模型,可以应用于需要定期维修的长贮装备,指导装备的科学维修,使长贮装备保持应有的高可靠性。
[1] 张永进, 赵明. 基于定期检测的贮存可靠性模型及其参数估计[J]. 系统工程理论与实践, 2008, 28(10): 82-88.
Zhang Yongjin, Zhao Ming. Storage reliability model and parameter estimate based on periodic inspection[J]. Systems Engineering -Theory & Practice, 2008, 28(10): 82-88.
[2] 徐廷学. 基于定期检测的导弹贮存可靠性研究[J]. 弹箭与制导学报, 2008, 28(1): 248-250.
Xu Tingxue. Study on storage reliability based on periodical test for missiles[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(1): 248-250.
[3] 张金春, 刘超. 定期检测对导弹武器系统贮存可靠性的影响分析[J]. 战术导弹技术, 2008(1): 44-48.
Zhang Jinchun,Liu Chao. Analysis of the influence of periodic check on reliability of missile weapon system[J]. Tactical Missile Technology, 2008(1): 44-48.
[4] 李大伟, 张志华, 刘天华, 钟强晖. 基于定期维护的产品维修策略研究[J].航空学报, 2013, 34(5): 1101-1107.
LI Dawei, Zhang Zhihua, Liu Tianhua, Zhong Qianghui. Product maintenance strategy research based on scheduled servicing[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1101-1107.
[5] Ito K, Nakagawa T. Optimal inspection policies for a storage system with degradation at periodic tests[J]. Mathematical and Computer Modeling, 2000(31): 191-195.
[6] 李青, 荣军. 长贮装备检测周期的优化研究[J]. 系统工程与电子技术, 1999, 21(8): 72-73.
Li Qing, Rong Jun. Optimal study on determining inspection period of long-storage equipment[J]. Systems Engineering and Electronics, 1999, 21(8): 72-73.
[7] Kallen M J, Noortwijk V J M. Optimal periodic inspection of a deterioration process with sequential condition states[J]. International Journal of Pressure Vessels and Piping, 2006, 83(4): 249-255.
[8] 王小林, 程志君, 郭波, 郭驰名. 基于冲击模型的劣化系统不完全维修决策[J]. 系统工程理论与实践, 2011, 31(12): 2380-2386.
Wang Xiaolin, Cheng Zhijun, Guo Bo, Guo Chiming. Imperfect maintenance decision for a deteriorating system based on shock model[J]. Systems Engineering-Theory&Practice, 2011, 31(12): 2380-2386.
[9] Huynh K T, Barros A, Berenguer C, Castro I T. A periodic inspection and replacement policy for systems subject to competing failure modes due to degradation and traumatic events[J]. Reliability Engineering and System Safety, 2011, 96(4): 497-508.
[10] 王永攀, 杨江平, 常春贺, 黄建军. 考虑定期维修的k/N系统维修资源配置方法[J]. 解放军理工大学学报(自然科学版), 2016, 17(2): 192-197.
Wang Yongpan, Yang Jiang ping, Chang Chunhe, Huang Jianjun. Maintenance resources configuration method for k/N systems considering regular maintenance[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2016, 17(2): 192-197.
[11] 张耀辉, 李林宏, 徐玉国, 郑毅. 基于关键零部件技术状态的机械产品定时维修间隔期优化方法[J]. 火炮发射与控制学报, 2016, 37(3): 92-96.
Zhang Yaohui, Li Linhong, Xu Yuguo, Zheng Yi. Optimization method of time-based maintenance interval for mechanical equipment based on the key part technical condition[J]. Journal of Gun Launch & Control, 2016, 37(3): 92-96.
[12] 罗吉庭, 熊志昂, 张全虎. 不可修武器贮存成败型数据可靠性预测模型和探讨[J]. 强度与环境, 1993, 89(1): 60-64.
Luo Jiting, Xiong Zhiang, Zhang Quanhu. Study of reliability predicting model for non-repaired weapon data is pass-faic data[J]. Strength and Environment, 1993, 89(1): 60-64.
[13] 刘飞, 窦毅芳, 张为华. 基于成败试验的导弹贮存可靠性Bayes分析模型[J]. 航空动力学报, 2007, 22(1): 102-107.
Liu Fei, Dou Yifang, Zhang Weihua. Bayesian model for missile storage reliability analysis based on success-failure test[J]. Journal of Aerospace Power, 2007, 22(1): 102-107.
[14] 吴和成, 葛仁福. 基于检测数据的指数型元件贮存可靠性的置信限[J]. 经济数学, 1997, 14(2): 83-87.
Wu Hecheng, Ge Renfu. The confidence limit of reliability for exponential type component based on inspection data[J]. Mathematics In Economics, 1997, 14(2): 83-87.
[15] 李彦彬, 府天洁, 刘成绪. 一种基于定期检测的导弹可靠度计算方法[J]. 四川兵工学报, 2011, 32(10): 1-3.
Li Ranbin, Fu Tianjie, Liu Chengxu. A sort of calculation method of missile reliability based on periodical inspection[J]. Journal of Sichuan Ordnance, 2011, 32(10): 1-3.
[16] 凌丹. 威布尔分布模型及其在机械可靠性中的应用研究[D]. 成都: 电子科技大学, 2010.
Ling Dan. Research on weibull distribution and its applications in mechanical reliability engineering[D]. Chengdu: University of Electronic Science and Technology of China, 2010.
Storage Reliability Prediction Method for Missiles UndergoingPeriodic Maintenance
Jiang Ping1, Xing Yun-yan1, Wang Bo1, Qi Jian-jun2
(1. College of Systems Engineering, National University of Defense Technology, Changsha, 410073;2. Beijing Special Engineering Design and Research Institute, Beijing, 100028)
Missile is usually maintained in storage in most of its lifecycle, during which periodic maintenance is often applied.Taking the potential impacts of the maintenance on the system storage reliability into account, based on the assumption that the lifetime of a missile follows Weibull distribution with initial failure, themost common scenario of failure rate increases while maintenance makes the system asgood as new, is taken into account. Corresponding storage reliability estimation model is presented, estimatesof the reliability before and after each maintenance are given, wherethe parameters are estimated by least square methods. Finally, based on the data of references, the presented models are demonstrated, and the results show that the models’ capability to predict missile storage reliability undergoing periodic maintenance.
missile; periodic maintenance; weibull distribution; storage reliability prediction
TB114.3
A
1004-7182(2020)02-0099-07
10.7654/j.issn.1004-7182.20200219
蒋 平(1976-),男,博士,副教授,主要研究方向为可靠性、安全性与装备综合保障。
邢云燕(1979-),女,博士,副研究员,主要研究方向为装备试验鉴定。
王 博(1997-),女,硕士研究生,主要研究方向为可靠性与装备综合保障。
齐建军(1983-),男,助理研究员,主要研究方向为可靠性与装备综合保障。
2019-01-10;
2019-06-16
国家自然科学基金(71371182,71871218);湖南省自然科学基金(2016JJ3027)

