螺栓连接结构的止口部位优化设计
杨 乐,王立强
螺栓连接结构的止口部位优化设计
杨 乐,王立强
(西安航天动力技术研究所燃烧、流动和热结构国家级重点实验室,西安,710025)
对某Φ1000mm金属壳体螺栓连接结构建立三维有限元模型,基于AWE平台首先分析了无止口结构设计对螺栓的受力影响,进而以计算机实验设计方法为基础,采用目标驱动优化设计,对有止口结构进行优化设计。计算结果表明,在螺栓安全系数确定的前提下,优化后的螺栓连接结构变形协调,螺栓部位应力分布合理,相比初始结构,螺栓Mises应力减少15.6%,部件质量减少0.8%,止口内径和宽度对螺栓的受力影响较大。
螺栓连接;止口结构;优化设计
0 引 言
固体火箭发动机的众多连接方式中,法兰连接作为一种通用的方式被广泛采用,其中连接螺栓成为整个连接结构设计中的关键部件,需要对其在固体发动机工作过程中的受力进行准确的分析,从而确保发动机工作的可靠性[1]。同时,在整体连接结构确定的前提下,采用更加合理可行的辅助结构,尽可能改善螺栓的受力状态,是螺栓连接结构中一个亟需关注的问题。止口设计作为一种开口部位的止动结构,主要起到限位作用,防止两个连接件转配时错位、产生断差。除此之外,止口设计对螺栓连接结构中螺栓的受力也起到明显的改善作用,但目前多是基于经验进行止口部位的结构设计,探寻最优的止口部位结构设计对于整个螺栓连接结构的设计有着积极的作用。
相对于传统的仿真方法,计算机实验设计方法(Computer Design of Experiment,CDOE)以其经济化的实现手段在各个领域得到推广应用[3],实现复杂结构的参数化识别及优化。依据一定的算法在可行域定位采样点,以最少的采样点数目,为后续的结果分析及处理提供最佳信息。Lasheras等[2]利用实验设计方法D-optimal设计方案,定位了最优采样点,用最少的实验次数达到了最佳的响应面拟合精度。Dornberger等[3]基于实验设计的采样点,利用神经网络和多项式响应表面模型近似目标函数,并以修正的遗传算法对涡轮叶片进行结构优化,获得了Pareto最优解。
首先基于有限元仿真(Ansys Workbench Environment,AWE)平台[4~6]对有、无止口结构的螺栓连接结构进行内压载荷作用模拟,对比分析螺栓的受力状态。随后针对有止口结构,以螺栓连接中螺栓的Mises等效应力和整个部件质量为目标函数,选取几何参数作为优化变量,进行止口部位的优化设计,得到止口设计参数对螺栓的受力影响。
1 初始结构分析
1.1 有限元仿真模型
法兰结构沿圆周具有对称性,同时整个法兰横截面受到均匀作用力,故选取包含单一螺栓的3D实体进行建模,并对其它微小圆角进行简化,以提高网格质量。图1为连接结构的三维模型,模型直径为Φ1000 mm,开口直径为Φ309 mm,所用螺栓规格为M18,接头形式包括无止口结构和有止口结构。
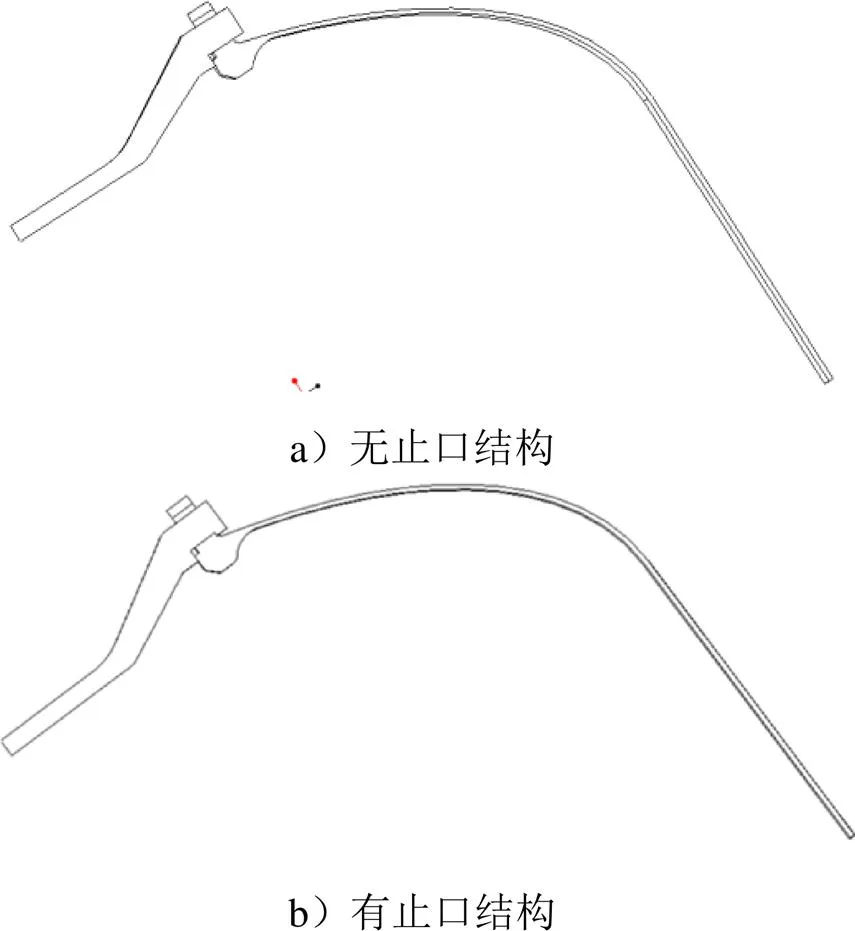
图1 三维模型
图2为有外止口结构对应的有限元模型,在进行有限元计算时,为进一步提高计算准确性及效率,对螺栓部位的网格进行了加密处理,其余部位网格则相对稀疏。整个模型的网格单元数量为7568个,节点数量为33 285个,通过网格质量检查,单元平均质量0.7,能够满足静力仿真要求。

图2 有限元模型
计算时在封头内表面添加压强边界条件,同时考虑对称性,将模型中两侧表面的法向位移以及筒段远端截面节点的法向位移设置为零,针对螺栓接触部位采用仿真软件中的虚拟螺纹功能。模型中连接螺栓、顶盖和接头的材料属性如表1所示,其中螺栓设计的安全系数为2.0。考虑弹塑性对模型的计算影响,对所有材料均采用双线性弹塑性本构关系,同时模型采用Solid186高阶3维20节点固体结构单元,以提高仿真精确度。
表1 模型材料性能参数
Tab.1 Material Parameters for Model
名称弹性模量/GPa泊松比抗拉强度/MPa屈服强度/MPa延伸率 连接螺栓2070.31370110013% 顶盖1960.3108083510% 接头2040.3160013208%
1.2 结果分析
计算得到了螺栓连接结构在内压状态下的变形结果。其中,无止口结构计算云图如图3所示,有止口结构计算云图如图4所示,分别显示了螺栓的Mises应力及塑性应变。
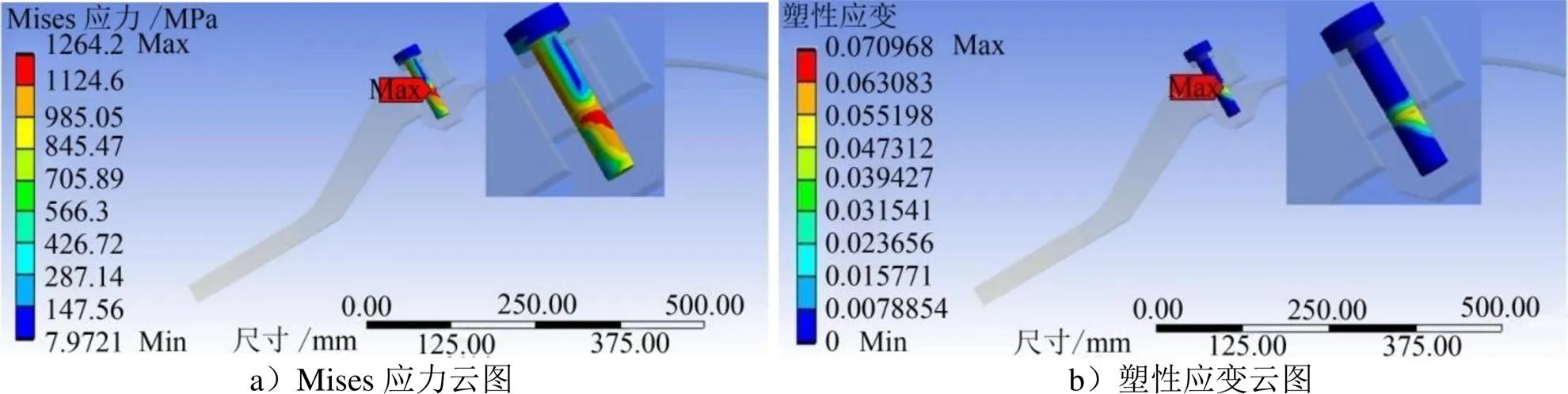
图3 无止口结构

图4 有止口结构
从图3a看出,无止口结构螺栓的最大Mises应力值约为1264 MPa,已超过材料的屈服强度,位置处于螺栓的中部。从图3b可以看出螺栓中部已经出现塑性变形,整个横截面塑性区接近贯穿,表明螺栓即将发生失效,整个连接结构安全裕度较低。图4a中有止口结构Mises应力最大值约为712 MPa,小于材料的屈服强度,位置与无止口结构相同。从图4b中看出整个螺栓未出现塑性变形,表明螺栓的安全裕度足够,止口结构对螺栓的受力状态改善明显。
2 止口结构优化设计
2.1 计算机实验设计方法
近年来,计算机仿真实验作为一种快速、高效的实验方法,在军事、航天、航空等领域有广泛的应用。其中,计算机作为辅助手段,如有限元(Finite Element Method,FEM)、计算流体动力学(Computational Fluid Dynamics,CFD)手段,已经在工程设计中得到广泛应用,但对于异常复杂的系统,仿真的时间成本也急剧增加,不利于快速解决问题。图5为结构设计中的常规的设计流程,基本思想为先采用FEM对结构进行强度分析,随后利用相关算法对结构进行优化设计,耗费的时间成本较大。

图5 传统结构设计流程示意
现代的计算手段引入计算机实验设计方法,极大的降低了优化计算成本,提高了设计阶段的工作效率。采用该种方法的流程图见图6,主要包含有4个步骤,其中的核心则是多学科分析及优化过程[7]。
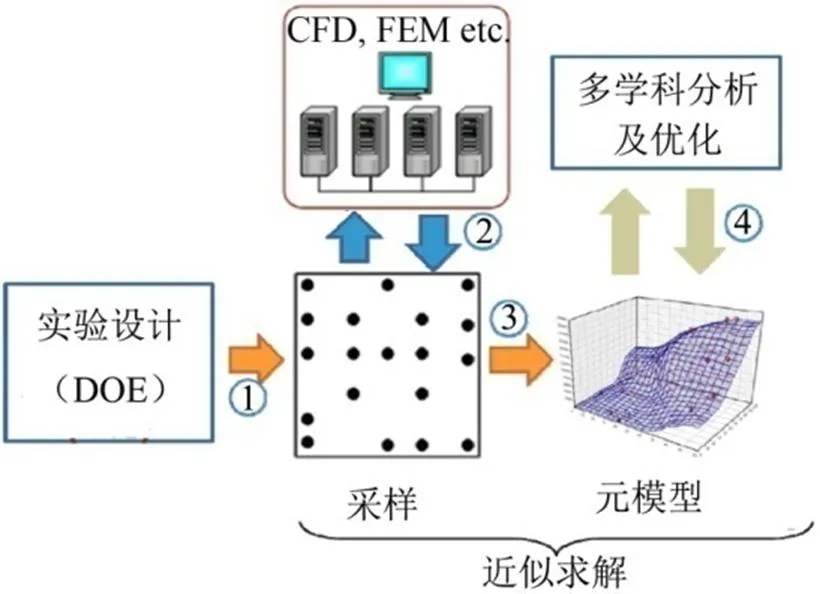
图6 计算机实验结构设计方法流程示意
作为目标优化设计,文中设置部件质量及螺栓部位结构应力作为目标函数,且要求在结构最大应力小于螺栓材料屈服强度的前提下部件质量的最小化。
2.2 模型设计变量
有止口结构的螺栓连接如图7所示,针对该止口部位进行结构优化,选取3个几何参数作为设计变量,包括有止口宽度、轴向深度、止口内径。

图7 几何参数示意
设计变量的初始值及搜索范围如表2所示。依据发动机总体及结构自身的设计要求,给出了各设计变量优化搜索范围,为实验设计的执行和优化算法提供采样空间边界。
表2 设计变量初值及搜索范围
Tab.2 Initial Value and Range of Design Variables
变量名称止口宽度/mm轴向深度/mm止口内径/mm 设计初值207473 搜索范围12~304~8472~476
2.3 目标驱动优化设计
目标驱动优化设计(Goal Driven Optimization,GDO)是一种多约束、多目标的优化技术,通过处理各个变量参数获得求解空间的最佳解,具体针对AWE仿真软件的参数化设计,则可以采用Advanced方法中的目标遗传算法[8,9]进行详尽的优化求解搜索。
基于Pro/e参数化建模平台和Ansys Workbench多目标参数优化模块的协同仿真来实现止口部位结构设计分析,分析流程如图8所示。选取螺栓的最大Mises应力和部件质量两个目标函数。

图8 目标优化分析流程
2.4 代理模型有效性校核
通常基于响应面的多目标优化结果(预测值)相比真值会有一定偏差。在多目标遗传算法中会得到3个侯选个体,采用仿真软件对所选个体进行计算,可获得各自的目标真值,优化预测值同目标真值的对比如表3所示。
表3 优化预测结果与目标真值对比
Tab.3 Contrast Between Optimal and Destination Value
对比项候选样本1候选样本2候选样本3 结构质量/kg最大应力/MPa结构质量/kg最大应力/MPa结构质量/kg最大应力/MPa 优化预测597.1611.7601.8625.2601.0622.9 目标真值598.2601.0599.7616.0591.8614.3 相对误差0.18%1.78%0.35%1.49%1.5%1.40%
由表3中的对比结果可见,优化预测结果对结构质量、最大应力两目标函数的真值具有相当高的一致性,最大应力位置均位于螺栓中部。3个侯选样本中,预测结果与真值相比,最大应力偏差为1.78%,最大质量相对误差为1.5%。同时,依据所选的二阶多项式代理模型推断,在设计选定的参数搜索空间内,可以认为设计变量对目标接近于二阶响应。
2.5 最优方案分析
由表3可知3个侯选样本结构质量相差较小,相对于模型初始质量603.2 kg,质量均有所降低,其中样本1中应力较大区域范围最小,故选用样本1作为止口部位的最终实施方案。表4给出了样本1的设计变量与原设计状态取值列表,结合图7,优化后止口宽度、轴向深度减小,在满足螺栓受力特性的前提下,整体结构质量有所减小。
表4 设计状态参数对比
Tab.4 Parameters Contrast of Design
变量名称止口宽度/mm轴向深度/mm止口内径/mm 设计初值207473 优选方案154.8474
初始及优化后螺栓的Mises应力分布云图对比如图9所示。由图可见,优化后结构质量减轻了约0.8%,最大应力为601.04 MPa,位置与原结构一致,都出现在螺栓的中部,且小于初始设计状态712.04 MPa,螺栓应力减少15.6%,表明优化后的结构更为合理。

图9 Mises应力云图对比

续图9
各尺寸关于质量和Mises应力敏感性分布如图10所示,止口内径相对于其余两个几何参数对Mises应力敏感度最为明显,随着半径的增加,应力值显著减小;止口宽度相对于其余两个几何参数对质量影响较大,随着宽度的增加,部件的质量有所增加。结果表明,止口内径和止口宽度为影响止口部位优化设计的关键参数。
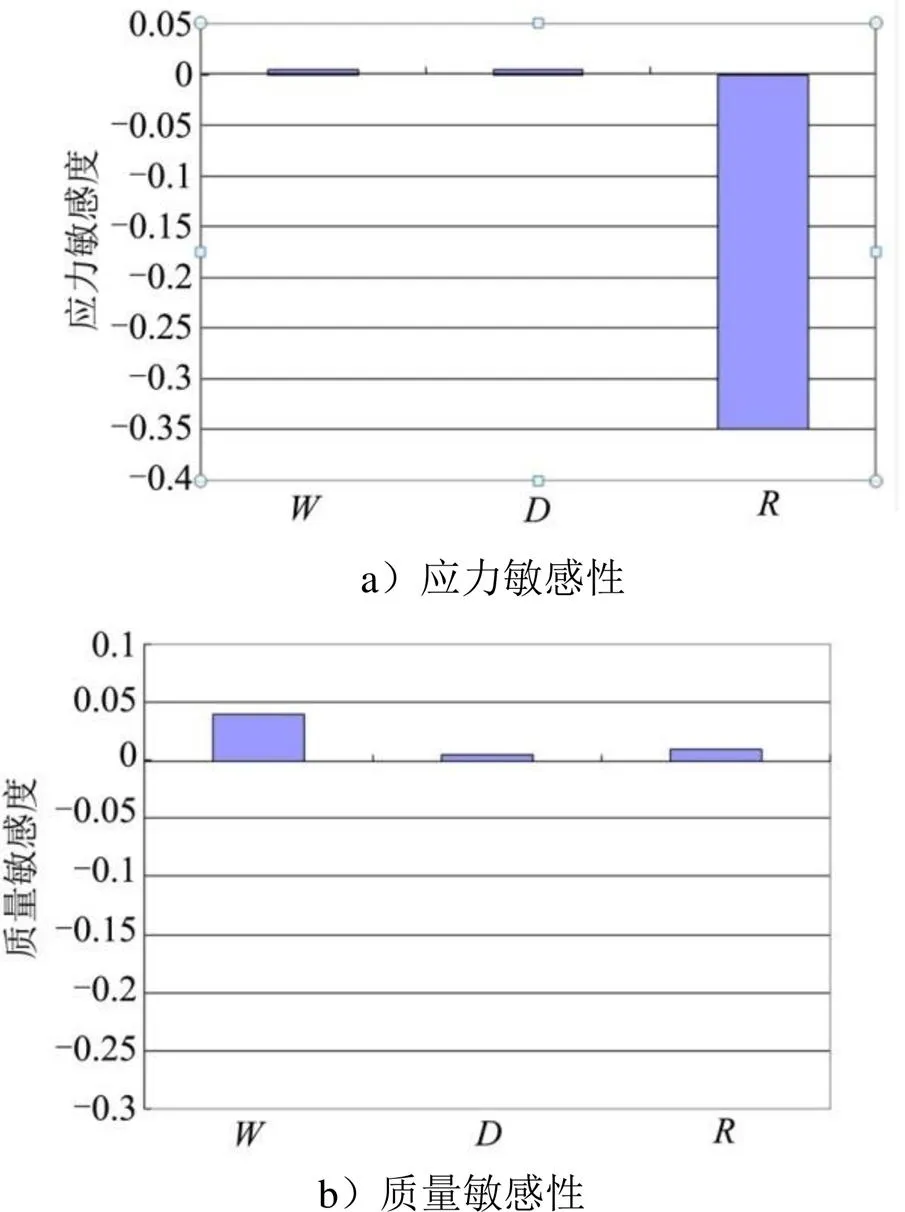
图10 参数敏感性分析
3 结 论
利用ANSYSWB/CAD-CAE协同仿真平台对有、无止口结构的螺栓连接进行了有限元分析,研究了有止口结构对螺栓受力特性的影响,同时对有止口结构进行了优化设计,结果表明:
a)在螺栓安全系数确定的前提下,无止口结构的接头螺栓受力更为恶劣,会出现螺栓发生塑性变形而导致连接结构失效的后果;
b)优化后的有止口结构会显著降低螺栓受力,与初始结构相比,螺栓Mises应力减少15.6%,部件质量减少0.8%;
c)通过对3个几何结构优化参数的敏感性分析,止口内径和止口宽度对优化结果影响明显。
[1] 任全彬, 等. 固体火箭发动机设计技术基础[M]. 西安: 西北工业大学出版社, 2016.
Ren Quanbin, et al. Design technology base for solid rocketmotor[M]. Xi’an: Northwestern Polytechnical University Press, 2016.
[2] Simpson T W, Toropov V. Design and analysis of computer experiments in multidisciplinary design optimization: a review bof how far we have come – or not[C]. Victoria: 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, 2008.
[3] Lasheras F S, et al. The use of design of experiments to improve a neural network model in order to predict the thickness of the chromium layer in a hard chromium plating process[C]. Mathematical and Computer Modeling, 2010: 3-7.
[4] 张岩. Ansys Workbench 15.0有限元分析从入门到精通[M]. 北京: 机械工业出版社, 2014.
Zhang Yan. The finite element analysis from entry to the maste of Ansys Workbench15.0 [M]. Beijing: Machine Industry Press, 2014.
[6] 黄志新. Ansys Workbench 16.0超级学习手册[M]. 北京: 人民邮电出版社, 2016.
Huang Zhixin. The study guide of Ansys Workbench 16.0[M]. Beijing: Post and Telecom Press, 2016.
[7] 付稣昇. Ansys Workbench 17.0数值模拟与实例讲解[M]. 北京: 人民邮电出版社, 2017.
Fu Susheng. The numerical simulation with instace of Ansys Workbench17.0[M]. Beijing: Post and Telecom Press, 2017.
[8] Aute V C. Single and multiresponse adaptive design of experiments with application to design optimization of novel heat exchangers [D]. University of Maryland PHD dissertation, 2009.
[9] 刘钢,孙侠生. 基于遗传算法的复合材料圆柱壳屈曲多目标优化设计[J]. 强度与环境,2008, 35(2): 36-42.
Liu Gang, Sun Xiasheng. Buckling multi-objective optimum design based on genetic algorithm for composite cylinder shell[J]. Structure and Environment Engineering, 2008, 35(2): 36-42.
[10] Lin Chuang. Documentation for ANSYS Workbench Release 11.0, Beijing: Post and Telecom Press, 2007.
The Fixing Structure Optimization Design on Bolted Connection
Yang Le, Wang Li-qiang
(National Key Lab of Combustion, Flow and Thermo-structure, The Xi'an Institute of Aerospace Power Technology, Xi’an, 710025)
Three-dimensional finite element model is used to analyze Φ1000mm mental case with bolted connection. Based on the AWE, the mechanical properties of the bolt without fixing are analyzed. Based on the CDOE, the fixing structure optimization design is analyzed through GDO. The results reveal that the optimized fixing structure is reasonable under the certain safety factor of bolt, the Mises stress of bolt is decreased by 15.6% and the weight of structure is decreased by 0.8% compared with the initial structure. The radius and width of the fixing are mainly influenced on stress of the bolt.
bolted connection; fixing structure; optimization design.
V22
A
1004-7182(2020)02-0049-06
10.7654/j.issn.1004-7182.20200210
杨 乐(1984-),男,高级工程师,主要研究方向为固体火箭发动机总体设计。
王立强(1984-),男,高级工程师,主要研究方向为固体火箭发动机结构设计。
2018-05-22;
2020-01-20

