高频指数强上涨趋势预测研究
周鑫
(四川大学计算机学院,成都610065)
0 引言
股票市场复杂多变,高风险与高收益并存。而预测股市走势,一直是广大股民和众多投资机构所关注的问题。但是由于股票市场具有极大的不稳定性和复杂性,且涨跌在一定程度上已经违背了价格序列所蕴含的统计规律信息。目前已有的方法策略均未能很好地进行预测。本文主要针对大多数的股票价格和指数的波动并不是很显著,同时考虑到资产的稳定增长,提出一种新的解决方案。
早期的股票预测算法主要对K 线图和其他技术指标进行分析,并预测股票走势,例移动平均线(MA)、随机指标(KDJ)、平滑异同移动平均线(MACD)、相对强弱指标(RSI)和能量潮(OBV)等。如刘叶玲等人[1]利用RSI、KDJ 和5 日平均线建立了非线性回归预测模型。随着数据挖掘、机器学习理论的完善和深度学习强大的拟合性能,越来越多的研究者希望用人工智能算法综合考虑各方面因素,对股票市场的交易给出一些建议。如Shunrong Shen 等人[2]、邬春学等人[3]、程昌品等人[4]利用支持向量机(SVM)、Ballings 等人[5]利用集成学习的方法对股票市场进行预测。Kai Chen 等人[6]、Selvin 等 人[7]、Nguyen 等人[8]利用深度学习方法建模。但是现有的方法不能很好地解决股票走势预测的问题,原因包括:①对于股票价格相对平稳的阶段,完全按照预测的结果进行高频交易会因为手续费导致亏损。②对股票价格大幅的涨跌的阶段,预测的准确性对总收益有巨大的影响。
基于上述分析,本文提出强上涨预测模型模型,主要的改进点有:①将问题定义为三分类任务。目前一般将预测股指趋势转换为有监督的二分类任务,即上涨和下跌。定义为三分类任务能有效减少由在股票震荡阶段频繁交易产生的手续费用。②使用代价敏感损失函数。通过加大对大幅涨跌阶段判断错误的样例的惩罚力度,提高对大幅涨跌阶段的学习效果。
1 数据和模型
本文的目标是在预测高频指数强上涨趋势时保证预测不要出现严重错误——即将强下跌趋势预测为上涨。为了比较本文提出的模型和过去股票趋势预测问题常用的模型在这一任务上的效果,本文共使用了3种深度学习模型进行实验。除了本文作者提出的用于预测使用Spatial Dropout 和Conv1D[9]的模型外,还有传统的使用CNN 层的模型、使用LSTM 层的模型和不使用代价敏感的损失函数的相似模型作为基线。
1.1 数据源及预处理
在股价预测任务中,我们定义x1,x2,x3,...xt,...作为指数序列,每一天的时间步中,本文共用了5 个指标xt=(ot,ht,lt,ct,vt),其中包括开盘价(ot),最高价(ht),最低价(lt),收盘价(ct),交易量(vt),简称为OHLCV。
本文使用的数据为2013 年1 月4 日到2017 年12月13 日的沪深300(CSI300)指数5 分钟OHLCV 数据(开盘价、最高价、最低价、收盘价、交易量),其中60%为训练集,20%为验证集,20%为测试集。输入深度学习模型用于预测的时间窗口为60 个,在时间窗口内按特征进行Z-Score 归一化。时间窗口的标签有三类,分别为强上涨,震荡和强下跌。本文将每一个时间步的收盘价和它后一个时间步的收盘价的变化率按从高到低排序,前15%标记为强上涨,后15%标记为强下跌,如公式(1)所示,其余标记为震荡。在3 个集合上都使用同样的方法进行数据预处理。

Lt代表xt的标签,代表tforward时间步(本文tforward的值设置为1,即下一个时间步)后股票指数的对数收益,训练集中的样本按照其未来回报rt以降序方式排序;在排好序的样本中前15%被标记为+1,即强上涨。后百分之15%被标记为-1,其余的样例被标记为0。
1.2 指数强上涨趋势预测模型结构
本文作者提出的模型由三部分组成,分别为Spatial Dropout 模块,Conv1D 模块和全连接层模块。模型结构如图1 所示。接下来笔者将说明为何使用这样的网络结构。
众所周知,深度学习模型很容易在训练的过程中产生过拟合,一般而言,应对过拟合的方法有两种——正则化和Dropout。正则化的原理是在损失函数中添加模型参数项,而Dropout 的原理是在训练时让部分输入数据失效,避免模型对一些在任务中贡献较大的神经元产生依赖,从而过拟合。Spatial Dropout 和普通的Dropout 不同如图2 所示,在训练的过程中,它会将上一层传来的多通道的数据依照指定的概率Dropout 其中几个通道的完整输入,而不是随机让输入失效。本文决定使用Spatial Dropout,因为在指数趋势预测中,使用的数据仅有五个特征,在这种情况下,Spatial Dropout 相比普通的Dropout 可以让我们的模型更好地学会利用剩余Channel 的特征的组合实现更鲁棒的预测能力。在测试的时候,Spatial Dropout 层不会工作,模型会使用所有的特征。这相当于一个另类的集成方法,在一定程度上可以提高模型的性能。
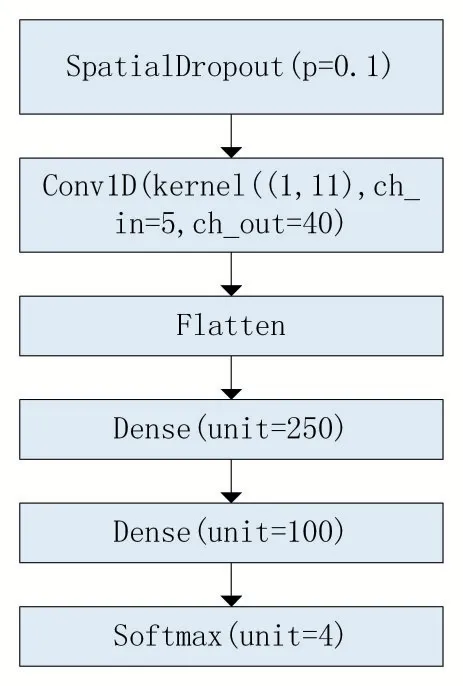
图1 指数强上涨趋势预测模型图
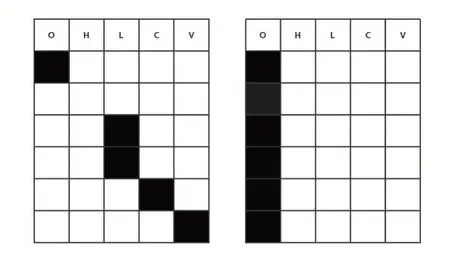
图2 Channel Dropout和普通Dropout
在卷积核的选取上,本文使用一层Conv1D 层。Conve1D 的卷积核为1×5,将输入的同一个时间步的5个特征映射为40 个特征,抽取深层信息。基于先验知识,本文认为预测指数的趋势,需要首先处理同一个时间步的OHLCV 信息,然后在考虑跨时间步处理数据。这与传统的CNN 图像分类任务不同,图像的像素点与它周边的像素点可以认为属于同一个流形,因此比较适合使用n×n 的二维卷积层处理信息。
同样是基于金融领域的先验知识——三浪理论,本文曾考虑后续使用n×1 的卷积核进一步提取跨时间步的更高维度的特征。然而,在验证过程中本文作者发现增加跨时间步的卷积层并不能提高模型在本文提出的任务上的效果。本文认为,三浪理论在高频数据中的有效性并没有得到证实,可能三浪理论并不适用于高频指数数据。因此,本文作者最终决定仅用一层Conv1D 作为卷积层。
在全连接层模块参数的选择上,本文使用超参数网格搜索,最终确定使用两层全连接层,第一层神经元数目为250,第二层神经元数目为100 的全连接层效果最好,输出层神经元数目为3,使用多分类任务中常用的Softmax 激活函数。
模型的损失函数使用代价敏感的交叉熵损失函数[10]。为了完成本文提出的任务——不将强下跌趋势预测为强上涨,本文作者在损失函数中含有强下跌输出的因子增加了放大系数α,α选择为1.25。本文作者希望模型在损失函数中对强下跌类别添加惩罚后可以降低将强下跌类分类为强上涨类的概率。代价敏感的损失函数公式如下:

1.3 基线模型结构
CNN 基线模型使用类似于AlexNet 的模型结构,拥有三层卷积层和两层全连接层和一层输出层,两层全连接层超参数与1.2 中提出的模型的全连接层的超参数相同。三层卷积层卷积核为都为3×3,将输入特征从5 个channel 映射到64 个channel。
LSTM 基线模型使用两个LSTM 层和两个Dropout层,两层LSTM 层分别将输入数据的channel 映射到32和64,两个Dropout 层的Keep Probability 为0.8,最后由两层全连接层和一层输出层输出各个类别的概率。
为了判断代价敏感的损失函数是否提高了模型在本文提出的任务上的效果,构建和1.2 小节中提出的强上涨趋势预测模型结构完全相同,只有损失函数使用传统的交叉熵损失函数的模型作为基线模型之一。
CNN 基线模型和LSTM 基线模型使用的损失函数与1.2 中提出的代价敏感的损失函数相同。
2 实验及分析
首先介绍实验数据集、评价方法和实验环境,其次对实验结果进行了分析。
2.1 数据集
本文使用的数据和数据的预处理、打标签方式见1.1 小节,数据集的具体分布和时间窗口内股指数据的图形化展示如表1 和图3 所示。
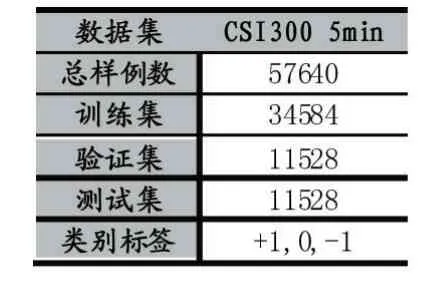
表1 CSI300 5min 数据集的分布

图3 时间窗口内的股指数据
2.2 评价标准
由于本文的目的在预测高频指数强上涨趋势时保证预测不要出现严重错误,因此,传统评价股指预测效果的评价指标如准确率不适合评判本文提出的模型在这一任务上的效果。本文提出了一种适用于评价此任务的评价指标:强上涨预测胜率。这一评价指标的定义如下:
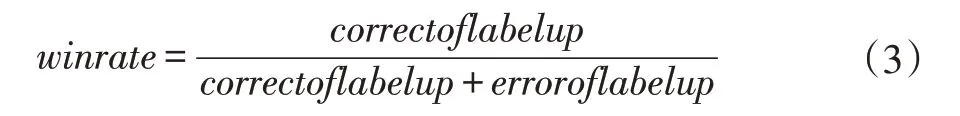
其中correctoflabelup 表示模型将输入的时间窗口的标签预测为强上涨时这个时间窗口真的是强上涨类别的数目,erroroflabelup 表示模型将标记为强下跌的时间窗口数据的标签错误预测为强上涨的数目。
2.3 实验环境
本文提出的模型和基线模型都使用TensoFlow2.0+Keras 框架构建和训练,优化器使用Adam 优化器,学习率都为0.0001。所有模型的参数都使用正态分布初始化,每个模型在训练过程中都随机打乱了训练集数据的顺序。由于数据集的不平衡特性,在训练时,为每个类别分配了相应比例的权重提高训练效果。
2.4 实验结果
强上涨趋势预测模型和不使用代价敏感的模型在CSI300 5 分钟数据集上的生成的混淆矩阵如图4所示。
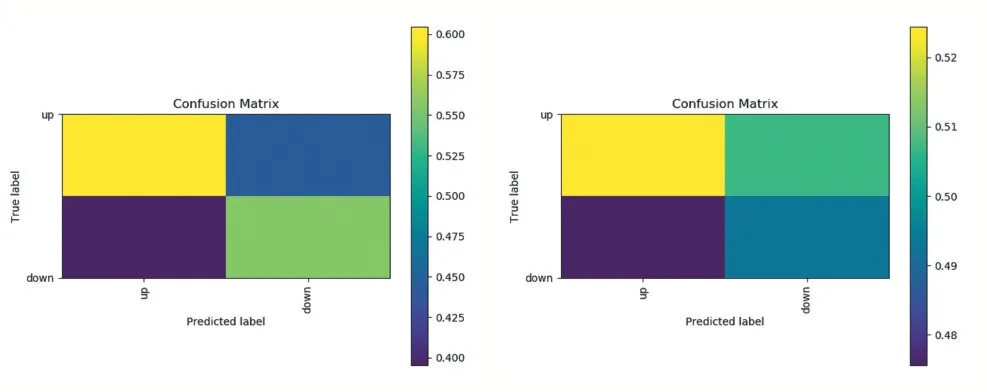
图4 本文模型和基线模型实验结果生成的混淆矩阵
四种模型在训练集和测试集上的强上涨预测胜率如表2 所示。
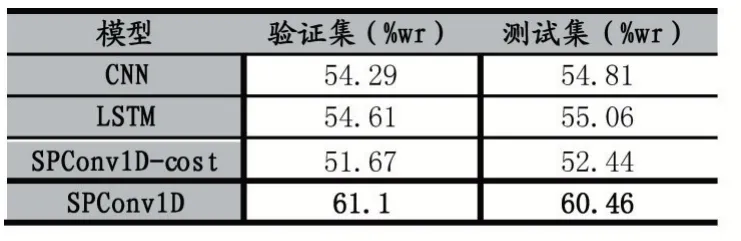
表2 CSI300 5min 数据集验证结果
2.5 结果分析
本节对本文模型使用的代价敏感的交叉熵损失函数在本文任务上的作用进行分析。
强上涨趋势预测模型和基线模型唯一的不同点在于是否使用了代价敏感的损失函数。然而图4 中,强上涨趋势预测模型的强上涨趋势的预测胜率实现了显著的提高,由52%附近提升到了60%。这说明使用代价敏感的交叉熵损失函数有效降低了将数据集中的强下跌标签误分类为强上涨标签的概率,充分说明了代价损失函数在本文提出的任务上提高胜率的有效性。
本节讨论本文提出的模型结构在本文任务上的优越性。
如表2 所示,本文提出的强上涨预测模型和传统CNN 和LSTM 模型对比,本文模型在CSI300(沪深300指数)数据集上的胜率比两种基线模型都要高5%左右。这充分说明了本文提出的模型使用的Spatial Dropout 层的效果,也说明了不考虑跨时间步生成特征的Conv1D 效果要优于传统的n×n 的卷积核。
3 结语
本文提出了在预测高频指数强上涨趋势时保证预测不要出现严重错误的任务,并设计了一个新的深度学习模型用于完成这一任务。在沪深300 指数5 分钟数据上取得了比两种传统的基线模型在这一任务上更加优越的结果。
本文的研究结果也具有一定的现实意义。由于金融市场交易成本的存在,每次交易都要付出交易额固定比例的金钱,在非强上涨的市场区间进行买入和卖出很难获得较高的收益。因此,理想的投资策略之一是预测未来会出现强上涨时买入金融资产。只要强上涨预测胜率足够高,这一投资策略就能获利。但是,高频指数的强上涨趋势上涨点数较小,还不足以使得投资者由此获利。未来将尝试在波动更大,更难预测单上涨点数也更大的股票数据上进行实验,实施模拟交易观察是否可以取得高于大盘走势的收益。

