城市干路行人过街警告标志前置距离研究
武腾飞,裴玉龙,徐慧智
(东北林业大学 交通学院, 黑龙江 哈尔滨 150040)
道路交通安全一直备受人们关注,道路交通事故高居世界卫生组织[1]所公布的十大“死因”之首,远高于艾滋病、自杀等其他因素,2013年,道路交通死亡人数已达125万人,其中的行人死亡人数比例为11%,也就是每年有12.75万行人死于交通事故。在城市道路系统中,行人过街与机动车冲突状况日益严重[2],保障行人过街安全尤为重要,除传统的宣传教育形式外,优化道路系统中的交通标志也成为一种必要手段,因此,开展城市干路行人过街交通标志前置距离研究具有重要意义。
近年来,交通标志设置问题已成为热点。夏佳等[3]基于路网拓扑结构,采用聚类分析及圈层覆盖等相结合的方法对指路标志设计过程进行建模,并通过算例分析验证模型的有效性;李爱增等[4]从驾驶心理学角度对驾驶员操作过程与车道转变过程进行微观分析,建立了城市快速路出口标志前置距离的理论模型;裴玉龙等[5]考虑了空间遮挡模型存在的缺陷,对交叉口路侧交通标志时间遮挡模型进行修正,建立驾驶人错过交通标志的概率模型;柏伟等[6]以指路标志作用机理及其在交叉口纵向设置影响因素入手,以车辆互相干扰最小为控制目标,建立交叉口纵向交通标志的选址概率模型;潘兵宏等[7]分析驾驶员在夜间环境下的视觉特性和认读特点,结合车辆前照灯照度特性、警告标志类型及特点,对夜间警告类标志前置距离进行研究,并提出建议值;孙小慧等[8]对旅游交通标志进行了研究,并综合考虑游客对旅游指路标志需求情况,以乌鲁木齐市南山风景区为例进行分析;张志清等[9]针对穿村镇公路因警告标志设置不当而造成的交通安全问题,结合驾驶员离散驾驶行为理论、心生理特性对穿村镇公路警告标志前置距离进行了优化;崔洪军等[10]针对高速公路出口前置指示标志(AGS)设置位置进行研究,建立了AGS安全设置距离计算模型。
目前,学者在指路交通标志设计过程、夜间警告标志及快速路出入口标志前置距离等方面做了较为深入研究,并取得了一定的研究成果,但对于行人过街警告标志前置距离研究较少,且《道路交通标志和标线 第2部分:道路交通标志》(GB5768.2-2009)(以下简称:第2部分)中对具体警告标志的前置距离也没有详细说明,仅要求设在警告地点前的“适当位置”。因此,本文在现有规范、标准的基础上,针对行人过街警告标志前置距离进行研究。
1 前置距离模型构建及解析
1.1 模型建立前的假设
在城市干路系统中,由于道路过长,所以应在其中间的适当位置设置行人过街设施,如人行天桥、地下通道、人行横道等位置。行人交通事故多发于人行横道处,因此一般在人行横道前都会设置行人过街警告标志。行人过街警告标志可为驾驶员提供良好的信息诱导,提醒驾驶员注意前方可能存在行人过街,应当减速行驶,避免意外发生。在实际生活中,人行横道上会有两种情况出现,存在行人或不存在行人。为使所得结果更加准确可靠,作以下假设:
1)研究部分的路面为直线路段,高差忽略不计,道路限速为60 km/h。
2)参与实验的被测试人员对交通标志的理解力都达到了正常水平。
3)参与实验的被测试人员严格遵守驾驶规则,在看到行人过街警告标志后进行决策并减速。
4)行人过街警告标志的设置位置等不受地理空间限制。
5)道路存在非机动车道,宽度为1 m;交通标志立柱底端距离路面边缘线为“第2部分”中规定的25 cm。
6)路上小汽车满足“第2部分”中规定的宽度为1.8 m,高度为2.0 m,成年人的坐姿眼睛高度为1.2 m。
1.2 驾驶员视认过程
驾驶员视认过程主要分为信息处理阶段、信息感知阶段、分析判断阶段、操作反应阶段四部分,详细划分驾驶员视认过程,将其分为看见标志、看清标志、读取标志、理解标志并决策、开始操作、标志消失6个过程,其详细视认过程如图1所示。
在A点,驾驶员看见交通标志,但未看清交通标志的具体内容,只是在头脑中有模糊意识;当车辆行驶到B点,驾驶员看清交通标志;在C点,读取标志内容;在D点,理解交通标志并决策;E点时,开始操作车辆,进行减速;F点,标志消失在视野中,这期间制动力会达到最大;此后做匀减速持续制动,K点车辆停驶在安全距离点。
1.3 模型构建
1.3.1 感知与判断距离
驾驶员在B点看清交通标志、C点读取交通标志、D点理解并决策、E点执行操作,这期间车辆速度v未改变,则感知与判断距离为
S1=v(t1+t2+t3).
(1)
式中:t1为看清标志到读取标志的时间,s;t2为读取标志并理解标志的时间,s;t3为操作反应的时间,s。
1.3.2 前视距离
前视距离,此处定义为当驾驶员看到交通标志时,交通标志在人眼水平高度上与道路中心面所成交点距离人眼的水平距离,如图2所示。

图1 驾驶员视认过程
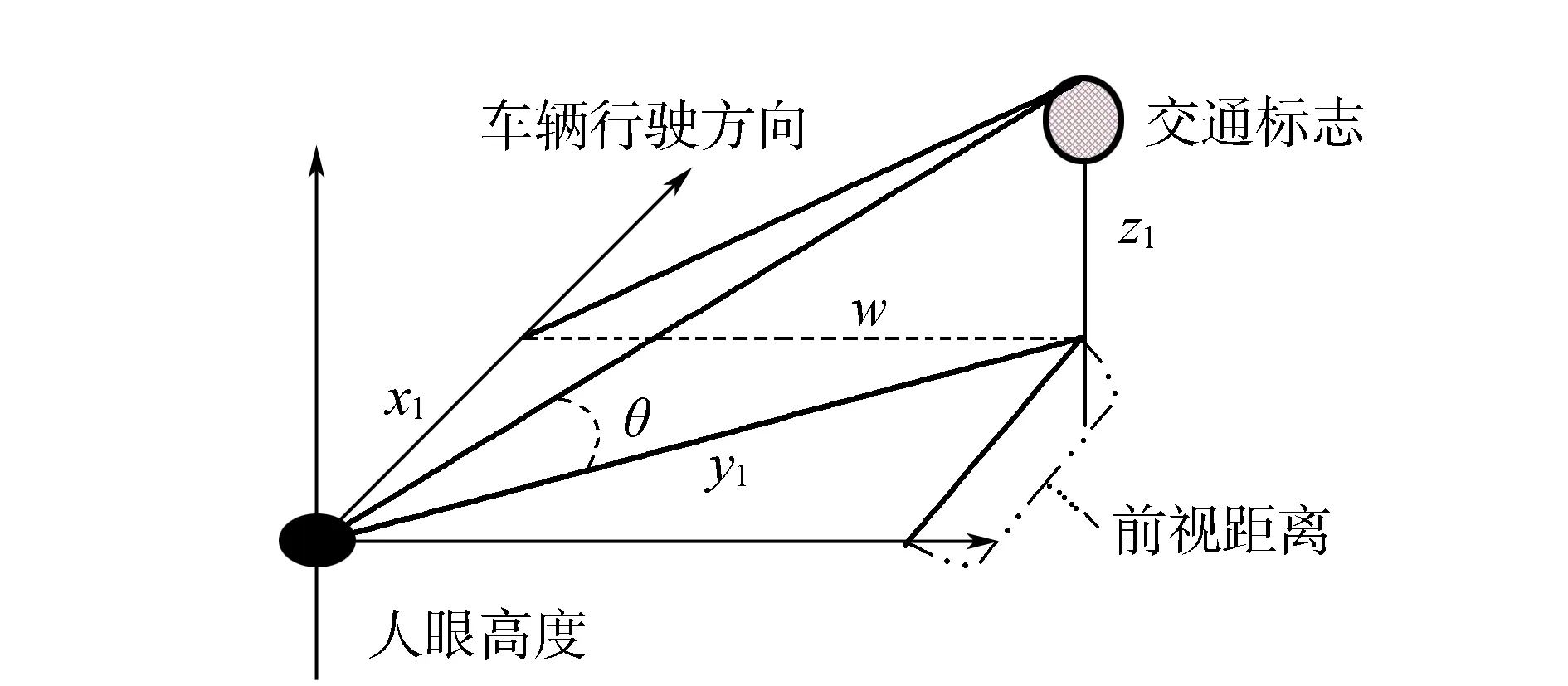
图2 前视距离
驾驶员在B点时看清交通标志,其水平视角与标志的上边缘线夹角为θ,杜志刚[11]认为当θ取值为8°时,驾驶员可准确认读交通标志,因此,在本文中取θ值为8°。交通标志设置在单柱式上,设其在垂直地面方向上距离人眼高度为z1,驾驶人与交通标志的视线水平距离为y1,交通标志垂直驾驶人正前方的距离w一般认为是车辆与机非分离线距离w1、标志底座距路面边缘线宽度w2、非机动车道宽度w3三者之和;等边三角形交通标志的边长为l;驾驶员的前视距离为x1。驾驶员看清标志时的抽象图,如图3所示。
w=w1+w2+w3,
(2)
(3)
式中:h为立柱式杆高,一般取值为1.50~2.50 m;0.20为杆底部与路面之间的高差,m;1.20为驾驶员坐姿高度,m。
(4)
(5)
S4=x1.
(6)
将式(2)、式(3)、式(4)、式(5)代入到式(6)中,得到驾驶员的视认距离,如式(7)所示
(7)
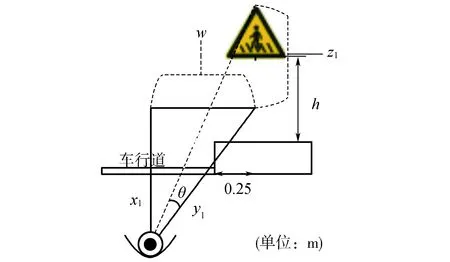
图3 前视抽象
1.3.3 交通标志可调整距离
交通标志可调整距离即驾驶员在决策后操纵车辆使其完全停驶在K点时的距离S2。交通标志可调整距离在《城市道路工程设计规范》(CJJ37-2012)(以下简称:“规范”)中为制动距离Sb,计算公式如式(8)所示,学者袁浩等[12]研究结果为S2,如式(9)所示。根据式(8)和式(9),对不同速度下的制动距离进行计算,结果如表1所示。
(8)
式中:V为设计速度,km/h;βs为安全系数,取1.2;μs为路面摩擦系数,取0.4。
(9)
式中:v为行驶速度,km/h;t′为制动力上升到最大的时间,取0.2 s;amax为最大舒适制动减速度,取3.4 m/s2。

表1 不同模型下的计算结果
由表1可知,当速度小于60 km/h时,S2始终大于Sb,但其差值不大;当速度为60 km/h时,S2等于Sb。本论文假设条件下速度不大于60 km/h,从安全行车角度考虑,更倾向于选择S2,因其提供的可调整距离更大。
1.4 模型解析
为保障车辆安全停驶在人行横道之前,需要满足前视距离S4与前置距离S之和不小于感知与判断距离S1、标志可调整距离S2、安全距离S3之和,即
S4+S≥S1+S2+S3.
(10)
将上述式(1)、式(7)、式(9)代入到式(10)中,得到行人过街警告标志的前置距离模型
(11)
式中:S3为安全距离,取值为5~10 m。
2 视认过程实验
2.1 驾驶员特征
对驾驶员进行视认试验,共招募20名被试者,其中男性12人,占比为60%,女性8人,占比为40%,被试者均已取得驾照且矫正视力处于正常水平、理解常见的城市干路交通标志,其年龄及驾龄分析结果如表2所示。在试验过程中,要求被试者在试验前一天保证充足的睡眠,不能饮用酒、刺激性饮料等以免影响视认能力。

表2 被试者年龄及驾龄特征
2.2 驾驶员认读时间
为获取驾驶员的认读时间,也即探究驾驶员看清交通标志到读取标志的时间t1。本过程拟采用如图4所示的方式进行试验。首先用电脑制作幻灯片,并将交通标志重复播放,共计16组,利用投影仪进行投影,根据人机工程学原理,被试者正坐于屏幕前并手持电子秒表。当实验者喊出开始时,被试者摁一下手中的电子秒表,使秒表进入工作状态;当交通标志出现且可被看清时,被试者摁一下电子秒表,此时刻为看清交通标志时刻,当可读取标志内容时,再摁一下电子秒表,此时刻为内容识别时刻,当被试者认读16组标志结束后,统计时间差值并记录。

图4 被试者认读过程抽象图
试验结束后,共计采集320条认读时间数据,一般认为认读时间在0.50~2.00 s之间。针对部分测试数据在0.50~2.00 s之外的情况,可能是被试者在测试过程中出现分神、精神高度紧张等所做出的误操作,其中大于2.00 s有21条数据,小于0.50 s有5条数据,共计26条,因此,其合格率达到了91.88%,统计结果如表3所示。

表3 被试者认读时间统计
2.3 驾驶员决策时间与反应时间
决策时间是指驾驶员在看到交通标志后,大脑决策是否采取措施所花费的时间。现有研究认为驾驶员的决策时间通常为1.00~2.50 s,在本文的假设条件下,认为驾驶员进行了操作反应,选取决策时间为1.50 s。
针对反应时间,于广鹏等[13]认为由于驾驶员反应程度不同,其反应时间取值范围为1.30~1.80 s;张智勇等[14]则认为在天气状况由晴朗到暴雨的过程中驾驶员反应时间变化率最大,其值在0.89~1.83 s,随着驾驶里程的不断增加,驾驶员的反应时间在0.87~1.72 s。综合以上情况,选取反应时间为1.50 s。
3 前置距离计算
根据“第2部分”规定,当道路设计速度为60 km/h、50 km/h、40 km/h,警告标志设置为等边三角形时,其边长l取值为0.90 m;当速度小于40 km/h时,等边三角形边长l取值为0.70 m;若受到空间限制时,等边三角形边长l可取最小值0.60 m。本研究中交通标志处于城市干路上,空间位置不受限制,故取等边三角形边长l为0.90 m、0.70 m。行人过街警告标志一般安装在单柱式的立柱上,且“第2部分”规定,立柱上交通标志的下边缘线距离地面的高度为1.50~2.50 m,本文中取最大值2.50 m。
“规范”规定,当道路设计速度小于60 km/h时,道路宽度一般为3.25 m。因此,当驾驶员行驶在第n条(n取自然数,且n≥1)车道上时计算w,则有
(12)
w2=1.00 m,
(13)
w3=0.25,
(14)
3.25+1+0.25=3.25n-0.375.
(15)
标定各个参数,结果如表4所示。将各参数及式(15)代入到式(11)中,则得到行人过街警告标志前置距离模型,如式(16)所示

表4 参数标定
(16)
将不同速度及车道数代入到式(16)中,得到不同速度、车道数(单向)下的行人过街警告标志的前置距离,如表5所示。由表5可知,当速度为60 km/h时,随着车道数增加,其前置距离分别为103.088 m、104.032 m、105.815 m,建议取值为104 m、105 m、106 m,给出的综合建议值为110 m;速度为50 km/h时,随着车道数增加,其前置距离分别为78.406 m、79.350 m、81.133 m,建议取值为79 m、80 m、82 m,给出的综合建议值为85 m;速度为40 km/h时,随着车道数增加,其前置距离分别为55.993 m、56.938 m、58.721 m,建议取值为56 m、57 m、59 m,给出的综合建议值为60 m;速度为30 km/h时,随着车道数增加,其前置距离分别为37.104 m、38.135 m、40.120 m,建议取值为38 m、39 m、41 m,给出的综合建议值为45 m;速度为20 km/h时,随着车道数增加,其前置距离分别为19.231 m、20.261 m、22.247 m,建议取值为20 m、21 m、23 m,给出的综合建议值为25 m。综上所述,当车道数一致时,随着速度的增大,其前置距离增大;当速度一定时,随着车道数增加,其前置距离会不断增大。

表5 不同速度、车道数下行人过街警告标志前置距离
4 结 语
本文就驾驶员视认过程进行分析,针对城市干路上行人过街警告标志的前置距离展开研究。通过考虑道路宽度、驾驶员特征、行人安全距离等因素建立了城市干路行人过街警告标志前置距离模型。通过模拟驾驶员视认过程试验,得到了驾驶员视认过程中的部分数据。最后,通过参数标定,计算了不同速度、不同车道数下的前置距离,结果表明,随着速度不断增大,标志的前置距离不断增加;同一速度不同车道数情况下,前置的变化值不大。未来将进行更加详细的试验,测定驾驶员的决策时间及反应时间,得到更加精准的行人过街警告标志的前置距离。

