Generating Periodic Orbits for Explorations of Elongated Asteroids

Huihui Wang, Yuntao Jiang, Long Xiao and Yonglong Zhang

(1.Beijing Aerospace Automatic Control Institute, Beijing 100854, China; 2.National Key Laboratory of Science and Technology on Aerospace Intelligence Control, Beijing 100854, China; 3.School of Aerospace Engineering, Tsinghua University, Beijing 100084, China)

Abstract: A practical method is proposed to search for periodic orbits of elongated asteroids. The method obtains required initial variables of periodic orbits by using the rotating mass dipole with appropriate parameters, and then implement local iterations to obtain the real orbits over an asteroid in the polyhedral model. In this paper the dipole and polyhedral models, and list detailed procedures of the searching method are introduced. A planar single lobe orbit is presented to evaluate the effectiveness of the method, with the asteroid 216 Kleopatra of the triple asteroid system as a representative elongated body. By applying the above method, ten families of periodic orbits around Kleopatra are identified and discussed with respect to their orbital stabilities and periods. One sample of the sombrero orbit is checked by calculating 1 000 hours to examine its orbital behavior. Besides the above orbits, the intriguing head-surrounding orbit is also analyzed.

Key words: periodic orbits; elongated asteroids; dipole model; numerical iteration

The precise polyhedral model[1]can be used to represent the gravitational field of a realistic small body. Since it seems impossible to derive analytic periodic solutions[2]for the polyhedral model, some numerical methods have been proposed to search for periodic orbits, such as the hierarchical gridding arithmetic[3]as an improvement of the grid searching method[4]. The hierarchical gridding arithmetic is very useful by obtaining 29 families of periodic orbits around the asteroid 216 Kleopatra categorized with their shapes. However, it took nearly 12 days to get the potential periodic results by using a PC with Intel Core i7 and the efficient FORTRAN code, and the results still need to be further examined with local iterations[3]. Most of the computing time was consumed by calculating the gravitational attraction step by step to forward the trajectory and searching for the large number of mesh points.

An alternative model with analytic expressions can decrease the calculation time. Reduction of the dynamic model has been previously tried by many researchers. Recently, Zeng et al. proposed a method to approximate the exterior potential distribution of natural elongated bodies with the rotating mass dipole[5].

Representatives of irregular shaped bodies, elongated asteroids or comets are the focus of this paper, whose potential will be simulated with two models, i.e., the dipole model and the polyhedral model. In this paper, large-scale periodic orbits will be estimated with the dipole model as the first step, which are adopted as the initial guess for the solutions around elongated asteroids. Local iterations are then performed to obtain the exact values of periodic solutions around the target asteroid with the polyhedral model.

The feasibility of the aforementioned two models can be illustrated from two main reasons. The first is that both models have the same form of dynamic equations and correspond to the Hamiltonian system resulting in the first integral of Jacobi constant. The second comes from the fact that topological structures around exterior equilibrium points of the two systems for sample asteroids coincide with each other[5]. Additionally, such a method is only to provide an attempt to solve the difficult problems in an easy way as the circular restricted three-body problem (CRTBP) was used to penetrate the three-body problem[6]. Particularly, the dynamic equations between the CRTBP and the dipole model hold the same mathematical form but slightly different potentials with only one different parameter which will be shown in Section 1. Thus, when we try to search for periodic orbits with the dipole model, the research methods and obtained periodic orbits about the CRTBP can be employed as references for the current problem.

1 Models to Determine Periodic Orbits

The rotating mass dipole model and the polyhedral model for the description of the gravitational field are briefly introduced in this section. The periodic orbits around natural elongated bodies is defined to illustrate the required parameters for the determination of an orbit. The state transition matrix is also derived, which is an effective way to determine the stability of a periodic orbit. A practical searching procedures is proposed to obtain periodic orbits in the near realm of an elongated body.

1.1 Rotating mass dipole and the polyhedral models

In this paper, two models will be adopted to study large-scale periodic orbits over natural elongated bodies, i.e., the rotating mass dipole and the relatively precise polyhedral models. The exterior gravitational potential of an asteroid or comet is first approximated by the rotating mass dipole model. The dipole model is composed of two point masses connected with a massless rod of constant lengthd. The phantom rod can provide compressive or tensile forces resulting in the two point masses in a fixed relative position. A body-fixed frame can be defined with its origin at the mass center of the dipole system as shown in Fig.1a.

Fig.1 Schematic map of the rotating mass dipole and equilibrium points of Kleopatra

Assuming the spinning velocity of the central body is constant, then the dynamic equations for the particle around such an elongated asteroid can be written as

(1)

where r is the position vector from the barycenter of the dipole to the test particle andUis the gravitational potential of the dipole system which can be given as

(2)

whereMis the total system massM=m1+m2andGis the gravitational constant in a value of approximately 6.67×10-11m3/(kg·s2);μis a scalar parameter representing the mass ratio between the second primary and the total system mass. The parametersr1andr2are the distances between the particle and the two primaries, respectively.

To simplify the calculations a canonical form of the dynamical equation, Eq.(1), is usually adopted. The dimensionless units are set to be

(3)

resulting in that the value ofGis unity. Moreover, the spinning period of the rotating dipole is 2π, the unit of the velocity isωdandω2dis for the acceleration.

Due to the conservation of the centrifugal term, Eq.(1) can be rewritten in a more compact form in dimensionless units

(4)

whereVis the effective potential defined as

(5)

and the vectorωin Eq.(4) is (0, 0, 1)T. Here, the scalar parameterκshould be specified as

(6)

The above term is usually referred to as “the force ratio”, representing the ratio between the gravitational force and the centrifugal force. It is interesting that whenκis exactly unity, the form of Eq.(4) is the same as that derived from the CRTBP. Similarly, the dipole system of Eq.(4) also admits the well-known Jacobi integral

(7)

which provides the boundary of the allowable area of motion from the view point of energy. Such a boundary is usually called the “zero-velocity surface” corresponding to the case ofC=V. It has been found that whenκ≤0.125 the non-collinear equilibrium points cannot exist anymore.

The required [κ,μ] of the dipole model is approximately [0.883 5, 0.486 3] to approximate the exterior gravitational potential distribution of Kleopatra[5]. Fig.1b shows the distribution of outer equilibrium points as well as zero-velocity curves in the equatorial plane. Note that the gravitational potential distribution inside the body’s surface cannot be approximated by the dipole model. Here, only the four exterior equilibria are given by neglecting the inner equilibrium point (or points). Thus, the name of these equilibria pinpointed withE1toE4is different from the traditional Lagrange points of the CRTBP.

The Jacobi integrals corresponding to the four equilibria are specified asCE2=-1.613 1,CE1=-1.603 2, andCE3=CE4=-1.256 2. The Jacobi integrals ofE1andE2are close due to the relatively high value ofμclose to 0.5. From Fig.1b, when the Jacobi integral of a particleC=-1.663 is less thanCE2, its allowable motion area in the equatorial plane will be separated into two parts. The inner part is close to the body’s surface where the particle will be finally down to the surface. The outer part is away from the surface by occupying a vast area.

All the four equilibria are located in the forbidden region shown with the shaded domain in Fig.1b. When the Jacobi integral increases to a value greater thanCE1, the forbidden region shrinks to two smaller areas including the non-collinear equilibria where the particle near the body’s surface can be admitted into the outer area. If the Jacobi integral keeps increasing to a value greater thanCE3, its motion is allowed in the whole equatorial plane. It indicates that periodic orbits in such conditions may be approaching the body’s surface in a very close distance.

The polyhedral model is only used in the final calculation of the potential of minor bodies. It can express the exterior gravitational potential and accelerations in a closed form. An irregularly shaped minor body should be first discretized into groups of faces and edges based on its exterior shape which was usually obtained with radar observations or vicinal explorations[7]. By using the Gauss formula and Green formula, the volume integral of the potential can be transformed into line integrals, resulting in the form of

(8)

whereσis the density of the polyhedron. Specific definitions of re, Ee,Lerelevant to edges can be checked from Werner and Scheeres[1]as well as rf, Ff,ωfrelevant to faces.

1.2 Searching procedures for periodic orbits

Periodic orbits and their detailed searching procedures with the dipole model has been studied[8], including the state transition matrix and the theory about orbital stability. After local iteration, the required periodic orbits with the dipole model have been obtained. Taking (w0,T0)Tas the initial values over a real asteroid, recalculate the orbit by replacing the gravitational potentialUin Eq.(2) with its correspondingUpin Eq.(8) obtained from the polyhedral model. Only a few iterations are required to obtain the final periodic orbit around the realistic central body by using the modified Powell’s hybrid algorithm[9].

2 Sample Orbits around the Dipole and Kleopatra

As a representative asteroid, Kleopatra is the subject of this paper as a central elongated body. The dog-bone shaped asteroid is the first to have a published radar shape model among the main-belt asteroids and received much attention to its composition and evolution[10]. With high resolution images, Descamps et al. confirmed recently that it is a rubble pile asteroid with an elongated integral body[11]. Hence, besides its practical value as a target of deep space explorations, searching periodic orbits around Kleopatra can help us to understand its triple system.

The polyhedral model of Kleopatra has been described in Ref.[3]. The spinning period is 5.385 h, and the overall dimension is approximately 225 km×98 km×85 km which is slightly different from the size provided by in Ref.[11]. The bulk density is then estimated to be 3.6×103kg/m3. The aforementioned parameters (κ,μ) of the dipole model, as given in Section 1, are (0.883 5, 0.486 3)[5], which will be used in the following simulations. The characteristic distancedof dipole model for Kleopatra is about 1.23×105m (122.996 7 km). The unit of the velocityωdis approximately 39.86 m/s.

In this section, the type of planar periodic orbit with a single lobe is taken as the sample orbit to show aforementioned method. Here, a brief comment is first made about the results presented by Ref.[3]. There are totally 29 intriguing families of periodic orbits categorized morphologically with the continuation by varying the Jacobi constant. Families 1-6 are local orbits associated to the local manifolds around the four equilibrium points. The near-filed double orbits of families 15-17 are essentially the continuation of local orbits around the equilibrium points[12]. A detailed analysis about the prograde equatorial near-circular orbits of family 14 has been made in Ref.[13]. All the above orbits have also been obtained in our simulations but will be omitted from the discussions below since large-scale orbits are the focus of our study.

2.1 Planar single lobe orbit

Similar to the CRTBP, Eq.(4) yields good symmetrical propertiesSas

(9)

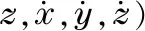
The single lobe periodic orbits around the dipole model are completely symmetrical but slightly twisted under the polyhedral model due to the nonsymmetrical potential field corresponding to the families 7 and 8[3]. The orbit in the solid line shown in Fig.2 is the sample orbit whose initial state variables are given in Tab.1. Based on Eq.(9), its corresponding symmetrical orbit is also given in the same figure in the dashed line. The schematic map of the rotating mass dipole is plotted in the center where the square marker on the orbit shows the starting point. All variables and the orbits in Fig.2 are in dimensionless units which can be easily transformed into the International System of Units with m, s and kg with Eq.(3). The searching angles can be clearly determined from the starting point withψ=0 and

in a value of 1.681 rad as the test particle flies in the retrograde direction. Since it is a planar orbit, the inclined angleθis zero.

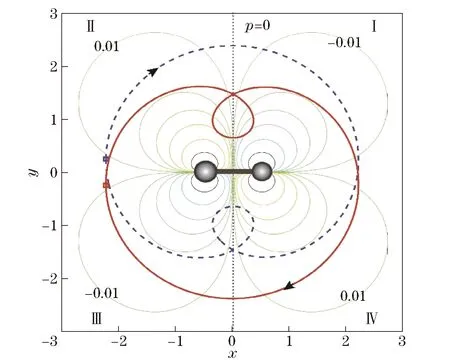
Fig.2 Single lobe orbit around the dipole model for Kleopatra in the body-fixed frame

Tab.1 Variables and periods of the single lobe orbit under the two models (dimensionless units)

One reason to choose the planar single lobe orbit as the sample is to show the influence of non-symmetrical distribution alongozdirection on the orbit. The second reason is that the dynamic characteristic of multi-revolution orbits (corresponding to the families 21-29 of Ref.[3]) is the same as this type of orbits. Such multi-revolution orbits will be introduced in the next section. The third is due to its symmetrical shape with respect to the zero line ofpwhose definition is

(10)

The scalar variablepis the energy changing rate referred to as the energy power[14]. There are two zero lines of the dipole model in the equatorial plane-one is aligned with the axisoxand the other is perpendicular to the axisoxwithx=1/2-μas shown in Fig.2. The four exterior equilibrium pointsE1-E4shown in Fig.1b should be located on these two lines.

The two zero lines separate the equatorial plane into four quadrants. The value ofpis negative in quadrants Ⅰ and Ⅲ and positive in quadrants Ⅱ and Ⅳ. A periodic orbit has to cross at least two quadrants with different signs, such as the local orbits aroundE4crossing Ⅰ and Ⅱ. For the sample orbit here, it is symmetrical with respect to the line ofp=0. Particularly, the orbital periapsis locates exactly on the zero line.

2.2 Discussions on the orbits and their stability

Fig.3 illustrates the real periodic orbit around Kleopatra corresponding to the initial orbit in Fig.2. These two orbits projected in the three planes ofxoy,xozandyozare given in dimensionless units to clearly show their difference. In the equatorial plane, the realistic orbit in the thick line nearly coincides with the initial orbit in the thin line around the dipole model. However, in the planes ofxozandyoz, there is a big gap between these two orbits along the direction ofoz. The real orbit ranges approximately 28.8 km (0.234d) out of the equatorial plane. Compared to the size of Kleopatra, the orbit covers nearly 33.88% of Kleopatra alongozdirection.

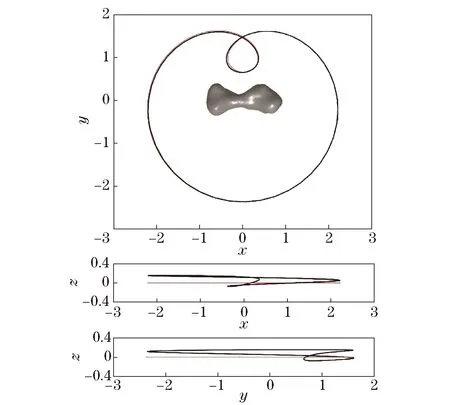
Fig.3 Realistic single lobe orbit around Kleopatra in the body-fixed frame

One reason is that the non-symmetrical distribution of Kleopatra alongozdirection has a great influence on the nearby orbit. Another possible reason is that the local iteration implemented by the Powell’s hybrid algorithm may not obtain the nearest real orbit. Such an effect could be checked by using other local iteration methods in further studies. Additionally, the dipole model cannot take the non-symmetrical distribution of a real asteroid alongozdirection into account. Hence, coupled effect of the above reasons along with the type of orbits result in the difference between the real orbit and its corresponding initial guess.

Besides the shape difference between these two orbits, the Jacobi integral is also slightly modified from the original -1.194 0 to the current -1.188 9 according to Tab.1. The period of the real orbit is about 10.56 h (12.321 4 TU) which is a little longer than the one around the dipole model. Although there are so many modifications of the real orbit, the type of its multipliers is the same as the original one with two pairs of real roots along with two roots of “+1”. Thus, these two orbits are unstable.

3 Families of Periodic Orbits Around Kleopatra

In this section some representative families of periodic orbits are obtained by using the above method.

More than two thousand potential peroidic orbits were obtained around the corresponding dipole model for Kleopatra. First, those potential orbits have to be checked whether interacting with Kleopatra. Second, local periodic solutions around equilibrium points are removed as they are out of scope of this study. Third, some repeated outputs with different section surfaces are removed from the list of interesting orbits. After the above screening and final iterations around the polyhedral model, 220 individual orbits are kept to show the orbital richness and complexity.

3.1 Example of periodic orbits

Ten families of periodic orbits are presented in Fig.4, including two quasi-equatorial groups and eight spatial families. They are simply categorized into six groups based on their geometrical structure. Some groups are illustrated via a piece of curved surface and only a representative orbit is given to show the accurate trajectory in the configuration space. For example, family (e) shows three dimensional double-lobe orbits including 13 samples. The upper and lower boundaries of the belt are two orbits while the inner and outer surfaces are distinguished by varying the depth of the color. As for family (i), only two sample obits are given among the total 11 retained solutions since it is difficult to show them with a unified curved surface.

Fig.4 Ten families of periodic orbits around Kleopatra

Family (a) shows the quasi-elliptical orbits in/around the equatorial plane with orbital periods ranging from 9.052 7 h to 10.659 9 h listed in Tab.2. The minimum radius (to the barycenter of Kleopatra) is approximately 167.310 km while the maximum radius is about 226.167 km. The type of multipliers of their monodromy matrices is also given in Tab.2. As there are a pair of real roots, all these orbits are unstable. In order to show their elliptical shape, a near-circular retrograde orbit is also plotted in the figure corresponding to a linearly stable orbit.

Families (b) and (c) are single lobe orbits with a small loop crossing the planeyoz. For family (b), the vertical motion near the body’s surface will be enlarged along with the decreasing of the orbital period. While for family (c) with the decrease of the orbital period, the apoapsis phase far away from the body’s surface will be driven up approaching the polar region of Kleopatra. Particularly, if we continuously decrease the orbital period, the orbit will be gradually converged to the local 8-shaped orbit associated to the sub-manifold of the nonlinear equilibrium pointE4. Another difference between these two families is the type of their multipliers although both of them are unstable. From Tab.2, a two-dimensional stable sub-manifold associated to the pair of complex number e±iβ(β∈(0, π)) is maintained by family (c) compared to the four-dimensional unstable sub-manifold of family (b). Additionally, it is easy to know that the sample orbit presented in Section 2 belongs to the family (b).

The dynamical essence of double-lobe orbits in family (d) is the same as the single lobe orbit of family (b) whose characteristics have been addressed in Section 2. The double-lobe orbits are highly unstable as the absolute value of its maximum multiplier can be up to 1.332 7×103. The particle running in such an orbit will be diverged to escape the near realm or collide with the surface of Kleopatra in averagely five orbital periods. In fact, once the periapsis of the orbit is changed away from the zero line of the energy power (i.e., the two loops symmetrical with the line ofp=0 are broken) due to the irregular gravitational attraction, then the orbit is quickly diverged. One should note that the multiplier type of family (e) with e±iβ(β∈(0, π)) is different from the other two families with two pairs of real roots.

Tab.2 Characteristics of orbits (A) to (F) around Kleopatra

A few sample orbits are shown in family (g) with different inclinations. The projection of these orbits in the equatorial plane is similar to the elliptical orbits or near-circular orbits. The largest angle of the inclined orbits shown here is approximately π/4. We evaluated that all these sample orbits have a pair of real roots e±α(α∈R,α>0) indicating such inclined orbits are unstable.

Compared to the above families of orbits in relatively simple shapes, a type of multi-revolution orbit, named the ”Sombrero orbit” for its hat-like resemblance, is categorized into families (h) and (i). A particle running in such an orbit is nearly on the surface of a sphere which has been shown in Fig.4. Only two families nearly symmetrical with respect to the planexoz(corresponding to (h)) andyoz(corresponding to (i)) are presented here while other sombrero orbits without symmetrical planes have also obtained but omitted from this paper. Note that the Jacobi integral of this family covers a wide range from negative to a positive value among other sample families. The orbits belonging to this family are also unstable due to the pair of real roots.

The last family named the “Neck-around orbits” is actually a local periodic orbits. They are like a necklace of Kleopatra over the neck-region. As is stated that the focus of this paper is the large-scale periodic orbits, this family is given here due to its interesting location as well as only one evidence that our program can obtain local periodic orbits. In analogy to the classical CRTBP, neck-around orbits should be a family of halo orbits around the collinear equilibrium pointL1. It has been revealed that Kleopatra has three inner equilibrium points besides the four outersE1-E4shown in Fig.1. If there were interstellar dusts orbiting around the neck of Kleopatra, they will be attracted to collide with the surface of Kleopatra or swept away to escape the near field since the orbit is unstable. At the meantime, there should be the 1∶3 resonant orbit which means that the period of the neck-around orbit is 1.795 h. For such an orbit, the particle circles three period while Kleopatra completes an exact revolution.

For all those orbits given in Fig.4, the type of multipliers of the monodromy matrix for the real orbit is the same as its corresponding initial guess around the dipole model although there is always a slight modification of its shape or location in the configuration space. It is impossible to numerically evaluate all periodic orbits to prove the invariance of the topological structure. Therefore, it indicates that the analysis of the periodic orbits around the dipole model can be used to understand the dynamical behaviors around natural elongated bodies, such as Kleopatra as well as some nuclear comets, i.e., 103P/Hartley-2, 67P/Churyumov-Gerasimenko.

Although those orbits are unstable, some of them can still fly around Kleopatra in a relatively long duration which has been reported by Chanut et al. with eccentric orbits[13]. Fig.5 illustrates an example by calculating one sombrero orbit of family (h). The state variables of the orbit are (-97.099 9, 132.294 6, 104.437 4)Tkm and (0.068 0, 0.039 4, 0.013 0)Tkm/s whose orbital period is about 11.061 5 h. An integration of the orbit for a long enough time, such as 1 000 h (>40 days) was performed to determine the propagation of the orbit[13]. It shows that a particle in such an orbit will still remain in the near field of Kleopatra by suffering the irregular gravitational attracting. For more accurate estimations, the perturbations of the solar radiation pressure force can be added to the current simulations. Particularly, if a spacecraft was inserted into this orbit, it would be advantageous for the surface coverage mission or the mapping of the accurate gravitational field of Kleopatra.

Fig.5 Propagation of one sombrero orbit around Kleopatra in 1 000 h

3.2 Unexpected case of the local iteration

Except for the above families of periodic orbits successfully obtained from the initial guesses, an unexpected case was also encountered during the local iterations.Fig.6 illustrates a sample orbit of this head-surrounding family in the dashed line. Obviously, it is a local periodic orbit. But the orbit’s local manifold is difficult to distinguish which equilibrium point it is affiliated to, the collinearE1or the inner one inside the head part[13]. Since the orbits close to the surface of Kleopatra has a complex shape, its corresponding converged solution obtained from the local iteration was not an orbit with similar shape. The real orbit around Kleopatra with the final local iteration is the well-known 8-shaped orbit aroundE1(the solid line in Fig.6).

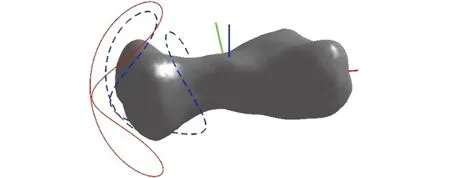
Fig.6 Head-surrounding orbit around Kleopatra in the body-fixed frame

The state variables and relevant parameters of those two orbits are given in Tab.3 in dimensionless units. Compared to the case shown in Tab.1, the differences between those two orbits are relatively big from the Jacobi integral to the orbital period. Although the type of their multipliers are the same, the distribution of these roots except the two “+1” is totally in different sides of the imaginary axis. For the failed case, we have obtained a class of head-surrounding orbits around the dipole model. With numerical iterations the converged solutions are 8-shaped orbits around the collinear equilibrium point of Kleopatra. It is hard to determine whether those head-surrounding orbits exist or not under the real gravitational field as our local iteration program cannot guarantee the least error between the initial guess and the final output.

In this section, ten families of periodic orbits classified in the configuration space have been presented by using the method proposed in Section 2. Those unstable orbits are categorized into five groups based on their shapes. Particularly, an example of the sombrero orbit is evaluated in 1 000 h which still remains in the vicinity of Kleopatra and not collides with the body’s surface. A “failed” case of the head-surrounding orbit (an unexpected solution) was also given due to its discovery for the first time. It is still an open problem for the existence of such type of real orbits as it was converged to the 8-shaped local orbit.

Tab.3 Variables and periods of the head-surrounding orbit (dimensionless units)

4 Conclusions

A practical method is proposed in this paper to efficiently obtain periodic orbits over elongated asteroids. The required initial six state variables and the orbital period are first obtained around the rotating mass dipole, which is used to approximate the exterior potential distribution of an elongated asteroid or comet. Taking those seven parameters as an initial guess, local iterations are then performed to identify the real orbits around the minor body. The method is efficient by obtaining ten families of periodic orbits around the representative asteroid Kleopatra, including single lobe orbits, double-lobe orbits, sombrero orbits and etc.

An unexpected case of the head-surrounding orbit has been also presented which is converged to the 8-shaped local orbit around the collinear equilibrium point. Although the periodic orbits given in this paper are unstable except the sample near-circular orbit, an integration of one sombrero orbit for 1 000 h were performed to identify that the orbit is still in the vicinal area of Kleopatra without colliding the body’s surface. Additionally, the method proposed in our study could also be applied to other elongated bodies, such as 103P/Hartley-2, 951 Gaspra, or 25143 Itokawa.