Pilot Contamination Elimination in Massive MIMO Systems with an Improved Time-Shifted Scheme

Yuanyuan Hao and Zhengyu Song

(1.Institute of Telecommunication Satellite, China Academy of Space Technology, Beijing 100094, China;2.School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044, China)

Abstract: Pilot contamination can bring up a grave impairment in the performance of massive multiple-input multiple-output(MIMO) systems. In this paper, an improved time-shifted pilot scheme is proposed to reduce the pilot contamination, where orthogonal pilots are employed in the same group to eliminate the residual intra-group interference existing in the original time-shifted pilot scheme. Meanwhile, the rigorous closed-form expressions of both downlink and uplink transmission rates with a finite number of antennas are derived, and it is shown that the intra-group interference can be completely eliminated by the proposed scheme. Simulation results demonstrate that both downlink and uplink transmission rates are significantly improved by employing the proposed scheme.

Key words: massive multiple-input multiple-output (MIMO); pilot contamination; time-shifted pilot

Massive multiple-input multiple-output (MIMO), which equips cellular base stations (BSs) with a very large number of antennas, has been demonstrated to achieve huge gains in spectral and energy efficiency with simple linear processing[1]. However, pilot contamination, caused by the inevitable reuse of finite pilot sequences among the cells, leads to a grave impairment to the system performance and persists even with an infinite number of antennas[2-3]. Therefore, efficient schemes to reduce pilot contamination are indispensable for massive MIMO systems.

There have been many studies on pilot contamination in massive MIMO systems[4-12]. In Refs. [4-5], BSs use low-rate coordination and additional second-order channel statistics to reduce the pilot contamination, while the complexity is related to the numbers of BSs and users. Blind pilot decontamination methods are presented in Refs. [6-7], which employ a nonlinear channel estimation based on the array gain. Although it is effective when the number of BS antennas is sufficiently large, the complexity of the singular value decomposition for the received signal block is extremely high. In Refs. [8-9], a pilot contamination elimination scheme is proposed based on the coordination of all cells. However, it operates in a complex training procedure and requires a long period of estimation time in proportion to the number of users of all cells, which is unrealistic in practical systems. Different from Refs. [8-9], an efficient time-shifted pilot scheme proposed in Ref. [10] requires much shorter estimation time, where all cells are divided into several groups and the pilot intervals at different groups do not overlap. The performance is analyzed in Ref. [10] with the assumption of an infinite number of BS antennas, and the case of a finite number of antennas is analyzed in Refs. [11-12].

Although the time-shifted pilot scheme can alleviate the damage from pilot contamination, the residual interference from the cells in the same group is still a performance bottleneck for the case of a finite number of BS antennas[11]. In order to eliminate the residual intra-group interference in the original time-shifted pilot scheme, an improved time-shifted pilot scheme, which employs orthogonal pilot sequences in the same group, is proposed in this paper. In comparison with existing elimination schemes in Refs. [8-9], a complex training procedure with the coordination of all cells are not required for the proposed scheme, and its channel estimation time is much shorter. Compared with Refs. [10-11], our proposed scheme successfully eliminates the residual intra-group interference and significantly improves the system data rate. Furthermore, the rigorous closed-form expressions of both downlink and uplink transmission rates are derived. Simulation results demonstrate that the system data rate can be significantly improved by employing the proposed scheme in comparison with the original time-shifted pilot scheme in Ref. [11] and the pilot contamination elimination scheme in Ref. [9].

1 System Model

Besides, a block fading model in time is assumed, where the channel stays constant over the block ofTsymbols, and varies randomly for each block. Consider a time-division duplexing scheme, assuming reciprocity between uplink and downlink channels, i.e., gjklis the same for both directions. Thus, each coherence block can be organized in three phases. At the first phase, each UT sends uplink pilots to BSs for channel estimation. Then, BSs transmit the pre-coded downlink data to their associated UTs at the second phase. Finally, all UTs transmit their uplink data to their BSs at the last phase.

Without loss of generality, the time-shifted pilot scheme is taken into consideration as shown in Fig. 1, where theLcells are partitioned into four groups, and the pilot intervals at different groups do not overlap. It is worth noticing that the time-shifted scheme relies on the assumption that the coherence blocks of different groups are asynchronous and start with their own first pilot symbol while cells in the same group operate synchronously.

2 Pilot Contamination Elimination Scheme

Since cells in the same group operate synchronously as shown in Fig. 1, the data rate with a finite number of BS antennas is still degraded by the residual intra-group interference[11]. In this section, an improved time-shifted pilot scheme is proposed, which employs orthogonal pilot sequences in the same group to eliminate the residual intra-group interference existing in the original time-shifted pilot scheme. Specifically, if there aren(n=L/4 in this paper) cells in one group, pilot sequences with the length ofτ=nKis used to ensure that the pilot sequences for UTs in the same group are orthogonal to each other. Letψikdenote theτ×1 pilot sequence, where the power of every pilot symbol is 1 and

(1)

i.e., pilot sequences for UTs in the same group are orthogonal to each other and reused in different cell groups.Without loss of generality,A1is chosen as the group of interest for the following analysis.

As shown in Fig. 1, during the uplink pilot phase forA1, thel-th BS in groupA1experiences the interference from other groups, and its received pilot signal can be expressed as

(2)

Thus, the estimated signal at thel-th BS can be expressed as

(3)

Theorem1In the improved time-shifted pilot scheme, the linear minimum mean square error (LMMSE) estimate of the channel vector gjk′lis given by

(4)

Proof The LMMSE estimate of the channel vector is calculated by[13]

(5)

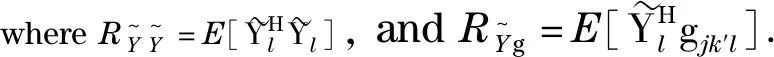
(6)

(7)

Remark1It is observed from Eq. (4) that the estimatejk′lis independent of all channel vectors except for gjk′l, which confirms that the pilot contamination is completely eliminated. In fact, the improved scheme can be treated as the pilot reuse with the reuse factorn. For the given pilot periodτ, a largernmeans fewer users in each cell, but the residual intra-group interference can be eliminated. Besides, it is more reasonable to have much shorter estimation time ofnKsymbols, compared with (L+1)Ksymbol in Ref. [9]. Moreover, the scheme in Ref. [9] operates in a complex training procedure with the coordination of all cells, while our proposed scheme is easier to be implemented.

3 Transmission Rate Analysis

In order to further verify the elimination of the residual intra-group interference by our proposed scheme, in this section, the rigorous closed-form expressions for both downlink and uplink transmission rates with a finite number of antennas are derived.

3.1 Closed-form expression for the downlink transmission rate

During the first part of the downlink data transmission phase of groupA1as shown in Fig.1, UTs in groupA2transmit uplink pilots to BSs while BSs of the other groups transmit the downlink data to their associated UTs. Thus, the received signal of thek-th UT located at celljin groupA1can be expressed as

(8)

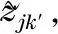
(9)

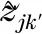
Theorem2The achievable sum rate per cell for the downlink transmission in Eq. (8) is given by

(10)

Proof Applying the method in Ref. [3] and according to Eq. (9), the achievable sum rate per cell for the downlink transmission can be expressed as

(11)

where the effective signal power is given by

Sjk′=ρfβjk′j|E[hjk′jwjk′]|2

(12)

and the effective interference and noise power is calculated by

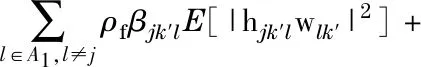
(13)

From the derivation in Ref. [3, Eq. (13)] and Eq. (6), the expectation term in Eq. (10) can be derived as

(14)

(15)

(16)

E[|ujik′k|2]=1

(17)

Finally, substituting the above results into Eq. (12) and Eq. (13), the conclusion in Theorem 2 can be proved.

3.2 Closed-form expression for the uplink transmission rate

For the uplink transmission, UTs from all cells synchronously transmit uplink data. BSjin groupA1is assumed to be the cell of interest, whose received signal can be expressed as

(18)

whereρurepresents the uplink data transmission power,qikdenotes the transmitted uplink data from thek-th UT in celli, and zjis the 1×Madditive noise vector. Then, BSjapplies the maximum ratio combination and the equalized signal can be obtained asjk′=yBjajk′, where

Since the channel information is available at the BS during the uplink transmission, the equalized signal can be expanded as

(19)

Theorem3The lower bound of sum rate per cell for the uplink transmission is given by

(20)

whereTuldenotes the uplink data length.

ProofFollowing the method in Ref. [15], the lower bound of sum rate can be denoted as

(21)

By using the property of a central Wishart matrix in Ref. [16,Eq. (2.9)], the following equation can be obtained

(22)

and the effective noise power is

(23)

Similar to the derivation of Theorem 2, the first expectation term in Eq. (23) is

(24)

and the other expectation terms in Eq. (23) can be derived as

E[|gikjajk′|2]=βikj

(25)

Substituting the above results into Eq. (21), the simplified result in Theorem 3 can be obtained as shown in Eq. (20).

Remark3Compared with Ref. [11,Eq. (28)],Njk′in Eq.(23) is independent of the number of BS antennas, which demonstrates that the residual intra-group interference is eliminated by the proposed scheme. When the number of BS antennasM→∞, the SINR for uplink data transmission also tends to infinity.

4 Simulation Results

In the simulations, our proposed scheme is compared with the original time-shifted pilot scheme in Ref. [11] and the pilot contamination elimination scheme in Ref. [9]. The cell radius is set to berc=1.0 km, and UTs are uniformly distributed in each cell except for a circle of 100 m around each BS. The default number of BS antennas isM=300. As the impact of pilot contamination can be significant if cross gains are of the same order of direct gains[3], we set all the direct gains to be 1 and all cross gains to 0.8, i.e.,βjkl=1 ifj=l, andβjkl=0.8 ifj≠l. Moreover, the transmit power isρf=100 W, andρr=ρu=10 W. For a fair comparison, the coherence block length is assumed to beT=105, and there areL=12 cells, andK=5 users in each cell for all the compared schemes. The length for pilot and downlink data transmission is

(26)

and

(27)

Besides, the uplink data length isTul=T-τ-Tdlfor all the schemes.

First numerical simulations are conducted to verify the tightness of our theoretical derivations. As shown in Fig. 2 and Fig. 3, both downlink and uplink achievable rates are tight. Then, in comparison with the original time-shifted pilot scheme in Ref. [11], both downlink and uplink sum rates per cell are significantly improved by our proposed scheme, due to the elimination of the residual intra-group interference. In addition, since longer estimation time is consumed by the pilot contamination elimination scheme in Ref. [9], the time for data transmission of their scheme is much shorter than our proposed scheme, leading to significant performance loss. Moreover, as the number of antennas increases, the data rate of the proposed scheme increases faster than the scheme in Ref. [9], while the original time-shifted pilot scheme is bounded by the residual intra-group interference.

Fig.2 Downlink sum rate per cell vs. number of BS antennas

Fig.3 Uplink sum rate per cell vs. number of BS antennas

Furthermore, the system performance is investigated for different numbers of users per cell in terms of downlink rate, uplink rate and total sum rate, where the total sum rate means the sum of downlink and uplink data transmission rate. It can be observed in Fig. 4 that the downlink rate increases while the uplink rate first increases and then degrades with the increase ofKfor both the proposed scheme and the original scheme in Ref. [11]. The reason is that whenKgoes up, both the length of pilotτand the downlink dataTdlincrease, while the uplink periodTuldecreases. More importantly, the proposed scheme always significantly outperforms the original scheme in Ref. [11] in terms of total sum rate.

Fig.4 Sum rate per cell vs. number of users

5 Conclusion

In this paper, an improved time-shifted pilot scheme is proposed to eliminate the residual intra-group interference of the original time-shifted pilot scheme, where orthogonal pilots are employed in the same group of cells. Both the rigorous closed-form expressions of uplink and downlink transmission rates are derived, and simulation results verify that the significant performance improvement is achieved by employing the proposed scheme compared with Refs. [9-11].