TIE和GS迭代算法用于生物细胞的相位恢复

于 颖，林大钧，王海凤

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

众所周知，物体的反射光包含了光的强度信息和相位信息[1]，通过CCD或COMS可以直接探测与收集光的强度信息，但是不能直接检测反射光的相位信息[2]。因此，许多学者提出了一些基于干涉测量的间接相位检测方法，例如全息术[3-4]、相位对比方法（PC）[5]、微分相位对比方法（DPC）[6]和微分干涉对比方法（DIC）[7]等。其中PC是最简单的实验方法，通常由传统的4f成像系统和空间光调制器（SLM）相互结合来实现相位恢复[8-9]。而DIC方法是一种光束剪切干涉技术，其中要求参考光束倾斜的量小于艾里斑[10]的直径。然而，由于相位和强度之间存在非线性关系，所以PC无法提供定量信息，而具有校准偏差的DIC技术也仅在精确对准后才能提供定量结果。还有一些非干涉方法用于恢复相位信息，例如光强度传输方程（TIE）、基于Gerchberg-Saxton角谱迭代（GS）算法等，可以通过仅收集在成像平面附近的2或3个图像的强度信息来恢复物体的相位[11]。通过求解二阶微分方程[12-13]可以得到物体的相位，目前对TIE常用的求解方式有傅里叶变换求解、Zernike多项式和多重网格（multi-grid）求解等。但是，TIE因为采用了太多的近似值导致精度值不高，而GS方法的初始相位是随机数，迭代时间较长。

鉴于上述情况，我们提出了一种新的方法，该方法通过结合TIE和GS算法来增强生物细胞图像的相位恢复的效果，并将其命名为GSTIE方法。我们先用TIE算法恢复出生物组织的相位信息，然后将得到的相位信息结果作为GS方法的初始相位，在经GS迭代后得到更加准确的相位信息。我们使用反射型显微镜，用白光照射生物细胞，在用CCD采集细胞的照片，并对采集到的3张图像分别采用GS-TIE方法恢复相位。在模拟仿真阶段，我们采用了红色、绿色和蓝色3个通道来对生物细胞进行恢复，以便获得最佳效果，该重建相位应该是3个重建相位结果之中的一个，这取决于所研究对象的主要颜色。对恢复对象的主色的判断可以帮助我们以最少的计算时间获得最佳的结果。

1 算法原理

1.1 光强传输方程

光强传输方程（TIE）是目前对垂轴强度图像进行相位恢复的著名工具[14]。图1为采用TIE方法收集的3张包含反射光强度信息的图像。

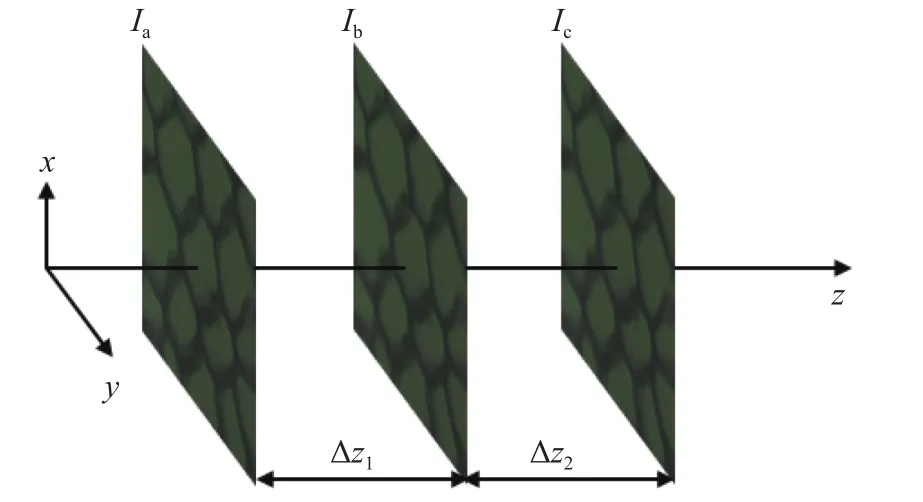
图1 TIE方法收集的3张包含强度信息的图像Fig. 1 Three images containing intensity information collected by the TIE method

TIE可以表示为

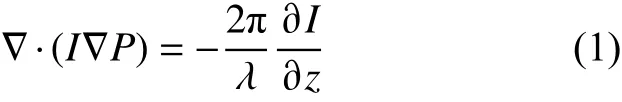
式中：I为光强；P为相位；z为间隔距离；λ为波长。

使用快速傅里叶变换方法可得到式（1）的解[15]。设每个图像平面上的衍射波强度分别为Ia、Ib、Ic，其中相邻平面之间的间隔为Δz，则3个平面的复振幅分别为：

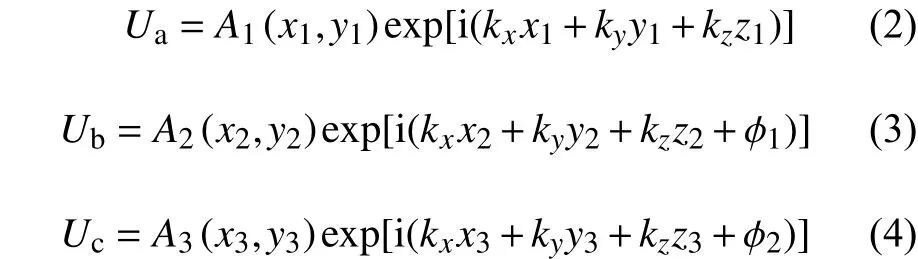
式中：A1、A2、A3分别为每个图像的幅度；kx、ky、kz分别为波矢量k在x、y和z方向上的分量；1和2分别为相对于第一平面的相位。

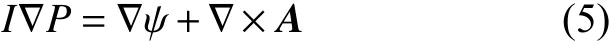
引用Teague近似，忽略式（5）的旋度项[16]，得 ∇，再对等式两边进行快速傅里叶变换。根据傅里叶变换的微分性质

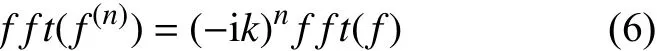
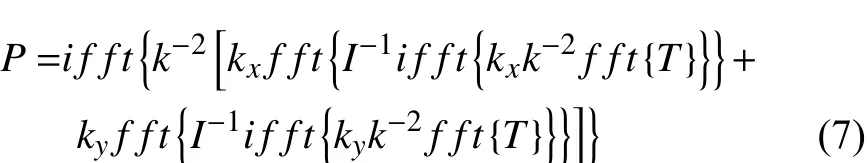
1.2 结合光强传输 方程（TIE）和 Gerchberg-Saxton迭代（GS）算法（GS-TIE算法）

GS-TIE方法主要包括两个步骤：（1）使用图1所示的3个平面中的光强信息获得相位分布，并将该相位作为GS迭代循环的初始值。（2）经GS迭代后获得精确的相位结果[19-20]。在GS迭代过程中，分别采用波长为λR= 625 nm、λG= 532 nm和λB= 473 nm的3个通道进行模拟仿真，进而得到3张相位恢复图。图2是GSTIE算法的流程图。两种方法的结合可以大大提高相位恢复的精确度。

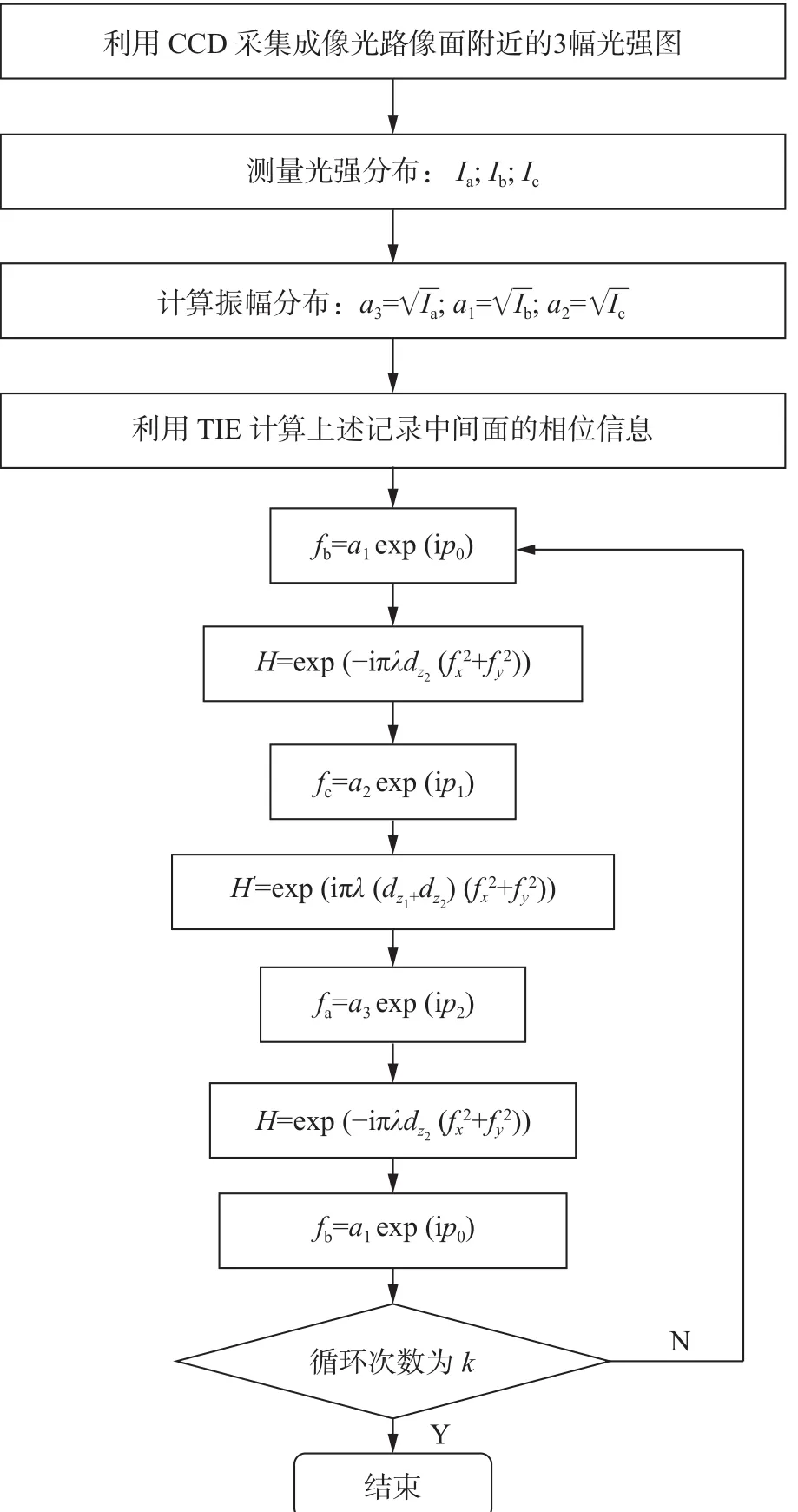
图2 GS-TIE 算法的流程图Fig. 2 Flow chart of the GS-TIE algorithm

将上述TIE计算所得的b面相位作为初始相位pb，结合模拟的b面振幅Ab，作为初始迭代面的复振幅fb带入迭代；利用快速傅里叶变换转换到频域进行处理，将其频谱乘以b、c面间距离Δz2对应的角谱传递函数，再进行傅里叶逆变换即可得c面的复振幅分布，通过对其求相位角以及记录所得的c面振幅Ac，重新构成c面的复振幅fc，对其在频域中进行角谱逆向传递，方法同第一步一致；如此每步用记录所得的振幅替代传播后计算所得的振幅加以校正。由此，衍射波传播过程记录的3个面形成一个循环，在传播到每一面时，用该面记录所得的振幅Ai(i=a,b,c)结合计算的光场传播到该处的相位pi(i=a,b,c)组成复振幅，这样可以校正光场角谱衍射迭代中的偏差。将实验测量数据的空间关联性更好地带入迭代运算中，从而得到恢复细节更好的b面相位pb。角谱传递函数的表达式如下：

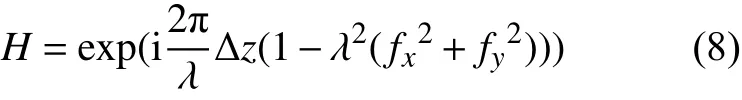
式中 fx=mx/Lx、fy=my/Ly，mx、my分别为 x、y 方向的空间频率采样系数，Lx、Ly分别为x、y方向的采样区间长度。

我们采用均方根形式对迭代算法的相位恢复进行了分析，所得该数值为两次循环的相位相对误差精度，其表达式为

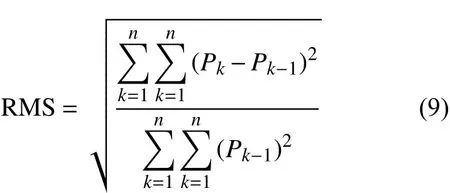
式中：n为迭代次数；Pk为迭代当次的相位分布；Pk-1为上次迭代的相位分布。

2 实验和结果分析

2.1 实验方法

我们在白光照射的反射型显微镜下用彩色CCD采集南瓜根茎样品细胞像平面附近的3个强度图像。显微镜物镜放大倍率为40倍，相邻图像之间的距离Δz。在采集图像强度信息时，如果间隔太小，相邻平面之间的光强差异不明显，如果间隔太大，将增加相位恢复的误差。通常，TIE算法要求采样的间隔约为1 mm。图3为在像平面附近以1 024像素×1 024像素的分辨率采集的3张根茎细胞彩色图像。

图3 像平面采集到的南瓜根茎细胞Fig. 3 Pumpkin rhizome cells collected in the image plane

2.2 实验结果

采用MATLAB软件进行仿真计算，将采集到的3张彩色图像逐一带入波长为λR= 625 nm、λG= 532 nm和λB= 473 nm的R、G、B 3个通道中，结果如图4所示。

从图4的通过GS-TIE算法恢复的3个彩色图像的相位图可以看出：G通道的相位轮廓最清晰，三维效果最明显，细节展示相对其他两个通道更为全面；R通道相对较弱，而B通道效果最不理想，噪点较多，3D效果较为模糊。图右边色条表示生物细胞的均匀程度。尽管如此，三通道相位误差的精度都高达10−7。图5显示了GS-TIE算法恢复的R、G、B通道的相对误差，图中横坐标为迭代次数（iteration time），纵坐标为相位相对误差值RMS的大小。

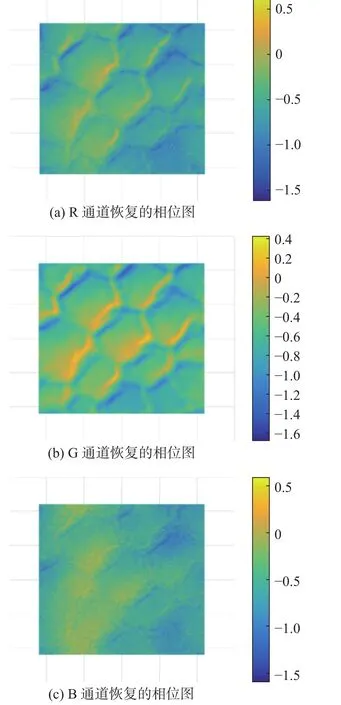
图4 RGB 三通道相位恢复图Fig. 4 RGB-channels phase recovery images

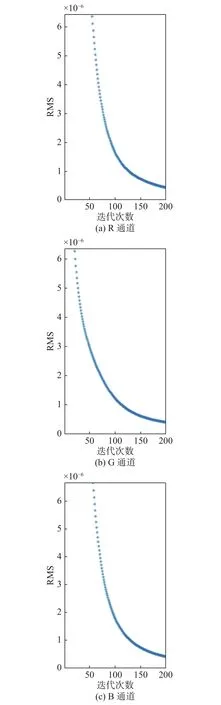
图5 GS-TIE算法恢复的RGB通道的精确度误差Fig. 5 Accuracy error of the RGB channel recovered by the GS-TIE algorithm

3 结 论

本文提出了一种利用白光进行生物组织图像高分辨率相位重建的新方法，该方法结合了强度方程传输（TIE）和 Gerchberg-Saxton迭代（GS）算法，并采用RGB 3个通道对生物细胞相位进行恢复。利用该方法，可以获得清晰的相位恢复图像，所得到的前后两次循环迭代的相位相对误差精度值可以达到10−7。