考虑实时拥堵指数和时间窗的多目标冷链物流配送路径优化

摘要：针对生鲜产品冷链物流配送时间和总成本最小化为目标，对配送中车辆使用成本、油耗以及碳排放成本等进行综合考虑。在实时拥堵指数和配送时间窗的约束下，构建成本最小化模型。并结合行驶过程中三个连续阶段的拥堵指数导致的行驶时间变化，从而得到优化策略;最后，基于Pareto支配接受准则的多目标模型进行求解，通过实际案例验证了模型的实用性和算法的有效性。结果表明，通过减少成本以及缩短时间来满足客户需要，将满足国家以及人民对冷链物流配送的要求。

Abstract： Aiming at minimizing the distribution time and total cost of cold chain logistics of fresh products， the vehicle use cost， fuel consumption and carbon emission cost are considered comprehensively. Under the constraints of real-time congestion index and distribution time window， a cost minimization model is constructed. The driving time caused by the congestion index in three consecutive stages during the driving process is combined to obtain an optimized strategy. Finally， the multi-objective model based on Pareto domination acceptance criterion is solved， and the practicability of the model and the effectiveness of the algorithm are verified by a real case. The results show that by reducing costs and time to meet customer needs， it will meet the national and people's requirements for cold chain logistics distribution.

关键词：冷链物流;实时拥堵指数;路径优化;模拟退火算法

Key words： cold chain logistics;real-time congestion index;path optimization;simulated annealing algorithm

中圖分类号：F259.2;X322                           文献标识码：A                                  文章编号：1006-4311（2020）09-0131-03

0  引言

随着经济的发展和居民生活质量的提高，人们对生鲜产品的需要也越来越高，同时对冷链物流的要求也越来越高。与传统的物流相比，冷链物流对运输产品的时效性具有更高的要求，此外，在考虑成本的情况下，也应降低行驶过程中对于车辆以及冷冻设备等产生的碳排放量。因此，本文在确保生鲜产品时效性的前提下，实现低碳运输，建立冷链物流配送模型。

1  问题的描述与模型建立

1.1 问题描述

已知L连锁超市生鲜配送中心的冷链配送车辆为同一车型，且车辆最大载重为Q，配送车辆以L连锁超市生鲜配送中心为起点，执行完配送任务后且再返回L连锁超市生鲜配送中心。假设L连锁超市的每个超市被且只被访问一次，配送车辆的最大装载量不能超过配送车辆的最大载重量Q，每个需被配送的超市都有一个时间窗，且不允许超过时间窗范围。本文考虑道路的交通拥堵和满足时间窗约束情况下，对冷链物流配送路径优化问题进行研究，考虑碳排放最低和配送时间最短两个目标。

1.2 假设前提

①配送网络中，顾客的需求量已知;

②车队只有一种运输车辆，其参数已经确定;

③车辆在途中不允许停留，不考虑货物装卸时间;

④顾客的需求必须被满足，并且顾客的需求不超过一辆车辆的总容量。

1.3 道路实时交通拥堵指数设置

根据车载GPS收集到的数据以及道路功能和流量等综合因素，换算成实时拥堵指数指标，从而用数值方式量化描述道路交通运行状态，提高道路交通运行状态表达精度，同时也达到一个指数值。无论对快速路、地面主干路或其他道路具有相同的拥堵含义描述。为了能更有效及准确的收集各路段的实时拥堵指数，本文路段的实时拥堵指数来自于百度智慧交通，百度智慧交通是基于百度地图海量的交通出行数据、车辆轨迹数据、位置定位数据挖掘计算所得，根据对各路段长久以来历史数据的收集，可以准确的预测出各个时刻路段的实时拥堵指数。

参考文献及计算方法，为设置合理的拥堵参数，以上海市为例，通过百度地图智慧交通数据，研究其交通拥堵情况，如图1所示，因考虑生鲜配送时间，图中仅研究从4：00-10：00的道路实时拥堵指数。

在模型计算中，根据周一至周五的拥堵指数按照以下标准规则，将实时拥堵指数与速度之间的关系对应起来，如表1。

1.4 参数变量

为了便于问题的求解，我们给出如表2所示符号说明。

1.5 车辆时间求解

1.5.1 实时拥堵指数变化时的行驶时间计算方法

一般拥堵情况下的行驶时间模型，在行驶过程中大致分为三个连续阶段：①拥有稳定速度vncon（变量）的正常行驶期，②拥有稳定速度vcon （常量）的拥堵期，③在两者之间的过渡期。车辆在行驶弧的距离d和离开时间l的计算如下式子所示：

上述式子中分别对应的行驶状况如下：式1）和式5）表示车辆处于正常自由行驶情况;式2）表示车辆处于由正常过渡到拥堵情况;式3）表示车辆处于完全拥堵的情况;式4）表示车辆处于由拥堵过渡到正常自由行驶的情况。

1.5.2 总行驶时间计算

在时变交通拥堵状况下，为了确定车辆在行驶弧（i，j）上的总行驶时间Tij，引入一个非负变量t■■表示

1.6 车辆成本求解

1.6.1 车辆的固定使用成本（人力成本+车辆使用成本）

使用车辆的固定成本通常是常数，与车辆行驶里程和服务的顾客数量没有关系，包括车辆的固定损耗以及驾驶员工资等与车辆使用相关的成本，设定为常数C1。

其中，Sk为0，1变量，Sk=1表示配送中心第k辆车被使用，否则Sk=0。

1.6.2 油耗（运输成本）和碳排放成本

为定量研究车辆燃油消耗和碳排放的计算，客户节点（i，j）的单位距离燃油消耗量ρ与车辆载重量Qx成线性关系可表示为：

已知配送车辆自重Q0，最大载重量Qk，设空载时单位距离燃油消耗量ρ0，满载时燃油消耗量ρ*，所以有：

得出：

可以得出，单位距离车辆燃油消耗量为：

可以得出客户节点（i，j）路段配送中所产生的燃油成本C2和配送中总碳排放量Qc表示为：

碳排放成本主要是描述车辆在配送过程中产生碳排放量的环境成本，本文通过燃油消耗来刻画车辆碳排放量，通过碳税机制定量计算碳排放成本，即碳排放成本=碳税*碳排放量，则在客户节点配送中的碳排放成本C3表示为：

1.7 目标函数模型

式（1）为目标函数1，代表车辆配送时间最短。式（2）为目标函数2，代表总的配送成本最小。式（3）为车辆运载能力约束。式（4）为配送车辆数量约束。式（5）为每辆车的配送线路起点和终点都是配送中心。式（6）和式（7）表示每个客户都需要被访问一次且只被访问一次。式（9）和式（10）是时间窗约束。

2  模拟退火算法

多目标优化方法：

通过对模型的分析，发现该模型有两个目标函数，时间最短和总成本最小。为求得多目标优化问题的非劣解常常需要將多目标优化问题转化为单目标优化问题去处理，实现这种转化，的经典方法主要有加权法，∈-约束法，进化算法等。多目标形式如下：

其中k？叟2表示目标函数同时最小化。本文是一个k=2的双目标优化问题采用以下形式：

为了产生尽可能多的生成 Pareto 最优解，每当右侧∈j有少量增加，问题也再次求解。因此，首先选择最小化总行驶时间为目标函数进行优化求解，然后把得到的总时间作为约束条件，对第二个目标函数进行优化求解。

3  算例求解

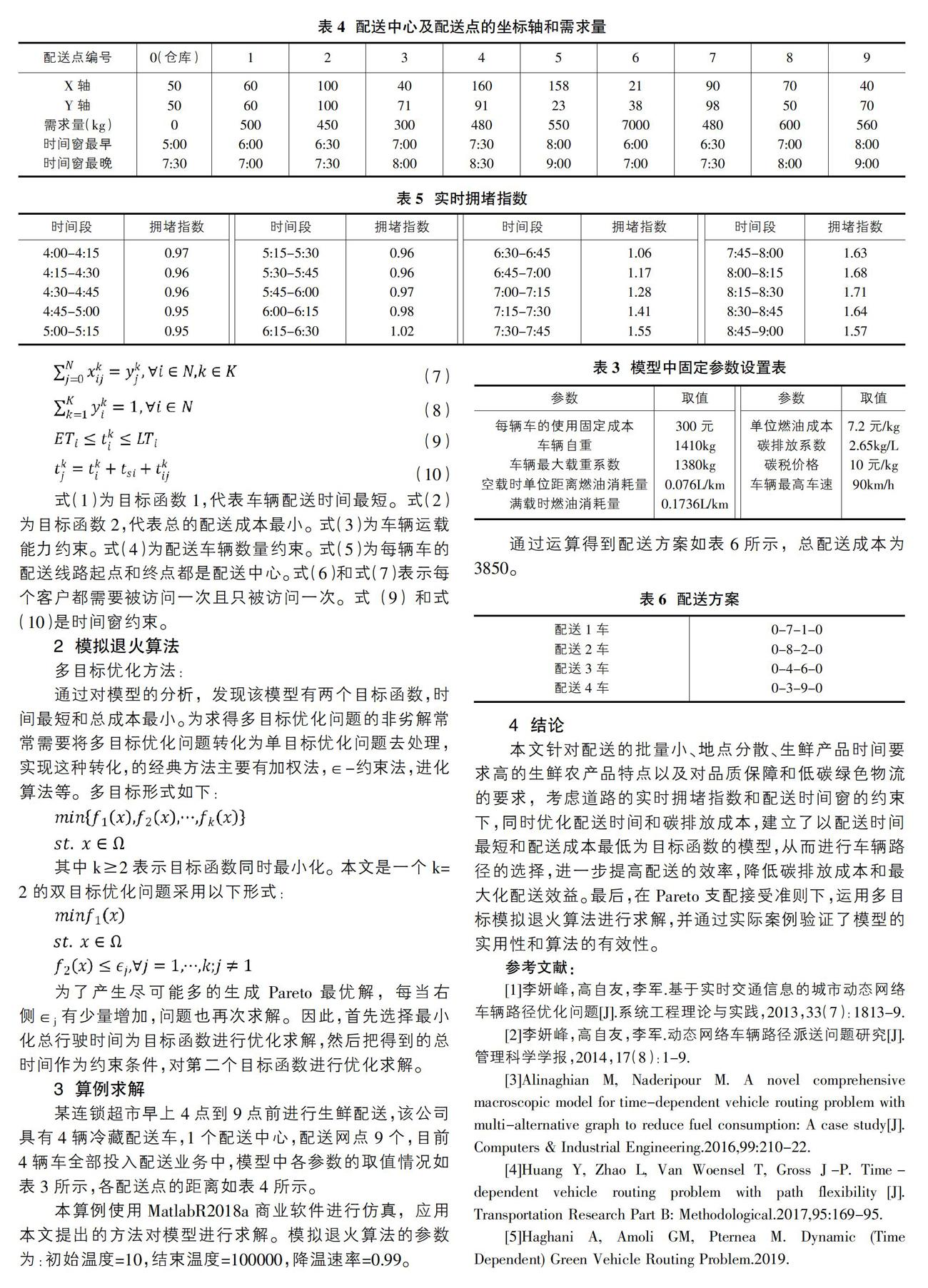
某连锁超市早上4点到9点前进行生鲜配送，该公司具有4辆冷藏配送车，1个配送中心，配送网点9个，目前4辆车全部投入配送业务中，模型中各参数的取值情况如表3所示，各配送点的距离如表4所示。

本算例使用MatlabR2018a商业软件进行仿真，应用本文提出的方法对模型进行求解。模拟退火算法的参数为：初始温度=10，结束温度=100000，降温速率=0.99。

通过运算得到配送方案如表6所示，总配送成本为3850。

4  结论

本文针对配送的批量小、地点分散、生鲜产品时间要求高的生鲜农产品特点以及对品质保障和低碳绿色物流的要求，考虑道路的实时拥堵指数和配送时间窗的约束下，同时优化配送时间和碳排放成本，建立了以配送时间最短和配送成本最低为目标函数的模型，从而进行车辆路径的选择，进一步提高配送的效率，降低碳排放成本和最大化配送效益。最后，在Pareto支配接受准则下，运用多目标模拟退火算法进行求解，并通过实际案例验证了模型的实用性和算法的有效性。

参考文献：

[1]李妍峰，高自友，李军.基于实时交通信息的城市动态网络车辆路径优化问题[J].系统工程理论与实践，2013，33（7）：1813-9.

[2]李妍峰，高自友，李军.动态网络车辆路径派送问题研究[J].管理科学学报，2014，17（8）：1-9.

[3]Alinaghian M， Naderipour M. A novel comprehensive macroscopic model for time-dependent vehicle routing problem with multi-alternative graph to reduce fuel consumption： A case study[J].Computers & Industrial Engineering.2016，99：210-22.

[4]Huang Y， Zhao L， Van Woensel T， Gross J-P. Time-dependent vehicle routing problem with path flexibility[J].Transportation Research Part B： Methodological.2017，95：169-95.

[5]Haghani A， Amoli GM， Pternea M. Dynamic （Time Dependent） Green Vehicle Routing Problem.2019.

作者简介：吴欣（1995-），女，安徽宿州人，硕士在读，研究方向为公路运输。