玛纳斯河流域上游融雪洪水序列变化特征分析

何朝飞， 陈伏龙， 张志君， 杨 宽， 何新林， 龙爱华,2

(1.石河子大学 水利建筑工程学院， 新疆 石河子 832000； 2.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室， 北京 100038.)

1 研究背景

冰川、积雪作为淡水资源的储备，在河川径流补给以及经济建设中具有重要的意义，特别是在西北干旱区，春季融水对缓解绿洲生态系统水资源短缺的矛盾具有重要作用[1]。同时，冰川和积雪的融化，也时常伴有洪水灾害的发生，这将直接导致人、财、物不计其数的直接损失，严重影响了经济社会的发展。近年来，随着人类活动的影响和环境气候的变化，加剧了干旱半干旱地区生态水循环的敏感度[2]，从而使洪水序列的随机独立同分布假设面临极大的挑战。

洪水趋势性演变特征规律直接影响到区域防洪安全，探究洪水变化规律就成为必不可少的工作，但由于水文序列的破坏，加剧了其演变的不确定性。陈伏龙等[3]通过对玛纳斯河流域上游径流特征进行分析，得到了气候变化是影响其变化的主要因素；在此因素的影响下，郑锦涛等[4]采用 Mann-Kendall及滑动 t 检验法确定了玛纳斯河流域径流的变异年份；凌红波等[5]分别就玛纳斯河流域各水文因素进行了非参数检验，诊断了其跳跃性变异特征，并用R/S 分析预测了其未来一段时间的变化趋势；丁文学等[6]在玛纳斯河流域基于条件概率分布模型的基础上，分析了年径流量的变化趋势。而这些研究大部分是基于气候变化对玛纳斯河径流变化的影响研究，而极少涉及到对洪水演变的分析。特别是近年来，新疆洪水频率及洪水灾害呈上升趋势[7]，这将严重威胁到人们的生产生活。因此，在气候变化背景下研究玛纳斯河流域洪水序列变化规律也显得尤为重要。

本文针对环境变化下的融雪性洪水[8]，综合运用Pettitt法、Lee-Heghinian法、加权滑动平均法和Mann-Kendall法分析水文时间序列趋势特征，可为玛纳斯河水利工程防洪度汛安全、防洪管理及工程设计建设提供一定的理论依据。

2 研究区概况与数据来源

2.1 研究区概况

玛纳斯河流域位于中纬度欧亚大陆中心(43°27′～45°21′N，85°01′～86°32′E)，地处新疆天山北麓，准噶尔盆地南部，具有明显的大陆性干旱气候特征。干流全长324 km，流域面积33 500 km2，平均气温为4.7～5.7 ℃。河流属于冰雪融水和雨水混合补给型，具有显著的垂直地带性，其中现代冰川主要分布在海拔3 600 m以上的天山山脉，冰川面积多年维持在608.25 km2左右，对河流的补给可以占到径流量的35.3%[9]。

2.2 数据来源及预处理

本文水文数据选取玛纳斯河流域出山口肯斯瓦特水文站(85°57′E，43°58′N)1957-2014年间的流域逐日径流量。经计算整理选取1957-2014年玛纳斯河肯斯瓦特水文站控制流域年最大洪峰流量(Q)以及年最大1、3、7 d洪量(W1、W3、W7)为数据支撑进行研究。

3 研究方法

3.1 突变点检测

采用Pettitt法和Lee-Heghinian法，揭示洪水峰量年际变化中的突变情况。Pettitt检验法[10]主要基于Mann-Whitney统计量Ut,N，检验同一个序列x(t)的两个样本，其公式为：

(1)

(t=2,3,…,N)

假设：

(2)

既“0”假设表示水文时间序列满足于同一分布，无变异点；非“0”假设表示在时间t前后子序列服从不同的分布模式，有变异点t。利用KN来代表显著变点t的最大值，并确定变异点的位置；P值为显著性相关概率，其公式为：

(3)

(4)

Lee-Heghinian检验法[11]是Lee和Heghinian在假定水文时间序列总体呈正态分布以及变异点τ的先验分布为均匀分布的情况下，推得其τ的后验分布为：

f(τ|x1,x2,…,xn)=

k[n/τ(n-t)]Φ[R(τ)]-(n-2)/2

(5)

(1≤τ≤n-1)

(6)

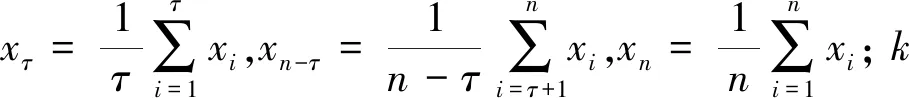
3.2 趋势性检验

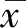
(7)

为了更加明显地判断时间序列的变化趋势，利用滑动平均法，绘制滑动曲线，从而直观地表示序列的变化趋势。

(8)

(j=1,2,…,n-k+1)

式中:k为滑动长度。在滑动过程中，由于滑动长度的设定，从而削弱了较短周期序列的变化幅度，进而体现出其整体趋势。本研究采用了13 a加权滑动平均，即为不同时间的要素值分配不同的权重，其滑动平均序列为[13]：

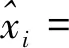
19xi+4+6xi+5+xi+6)

(9)

采用Mann-Kendall(M-K)非参数检验[14]，给定置信水平α，利用Kendall秩次相关系数(U)为数值依据，定量的分析序列在某一时间段内上升或下降趋势，并根据设定的临界值判断其是否显著。

4 结果与分析

4.1 峰量趋势变化分析

1957-2014年玛纳斯河肯斯瓦特控制流域最大洪峰流量Q的距平时间序列如图1所示。由图1(a)可看出，玛纳斯河流域Q的距平值在1994年以前大多为负值；1994-2004年这11年，除了1995年和2003年以外，其余均连续出现正距平值。距平序列的最大值出现在1999年，高出基准期洪峰值743.79 m3。从距平值的滑动平均曲线可以看出，玛纳斯流域Q在1970s到1990s中期经历了一个由下降到突增的过程后，开始呈现出明显下降趋势，且进入2000-2005年，下降幅度尤为明显。图1(b)表明，在1957-2014年间玛纳斯流域Q值整体呈现上升趋势但并不明显，同时可将其分为3个阶段：1957-1992年为下降期；1993-2005年为上升期，期间稍有波动；2006年之后为平稳期。

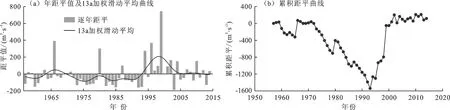
图1 1957-2014年玛纳斯河肯斯瓦特控制流域年最大洪峰流量距平变化

图2为玛纳斯河肯斯瓦特控制流域1957-2014年最大1、3、7 d洪量距平的时间序列。由图2(a)可看出，年最大1、3、7 d洪量在1957-1998年也整体表现出明显的上升趋势，但自1999起有较为明显的下降趋势且在本年出现了最大距平值。不容忽视的是，年最大1、3、7 d洪量距平值在近两年有所降低，说明玛纳斯河流域的洪量将面临着下降的可能。滑动平均曲线表明：年最大1、3、7 d洪量总体可分为4个阶段，在1971年之前较为平稳，1971-1991年有所下降但是趋势并不明显，从1992-1998年有较为明显的上升趋势，随后从1999-2014年期间稍有波动但整体趋于平稳。

从图2(b)中可以很直观的看出年W1在1993年与1995年处均出现转折，而W3、W7这个转折变异点发生1995年。从总体来说洪量的累积距平曲线大致可分为4个阶段。1957-1971年为平稳波动期；1972-1995年呈现出明显的下降趋势，其中在1987-1988年略显平缓，以W7尤为明显，而W1则在1995年出现较为明显的上升现象；1996-2003年为直线上升趋势；2004-2014年总体呈上升趋势但波动较大，值得注意的是最后两年均呈现明显下降趋势。就整体水文序列而言，运用M-K法求解其U值，见表1。M-K法统计量U值均小于1.96，说明了洪峰洪量序列的上升趋势并不明显。

表1 整体水文序列M-K统计值

4.2 变异点检测

采用Pettitt统计检验方法，分析玛纳斯河肯斯瓦特控制流域融雪洪水特征序列发生的突变年份如图3所示，概率P值超出0.95的年份，可认为是突变年份。Q的可能变异年份为1992、1993、1994和1995年；W1可能在1992、1993、1995年发生变异；W3可能在1993、1994、1995和1996年发生变异；W7可能在1994和1995年发生变异。

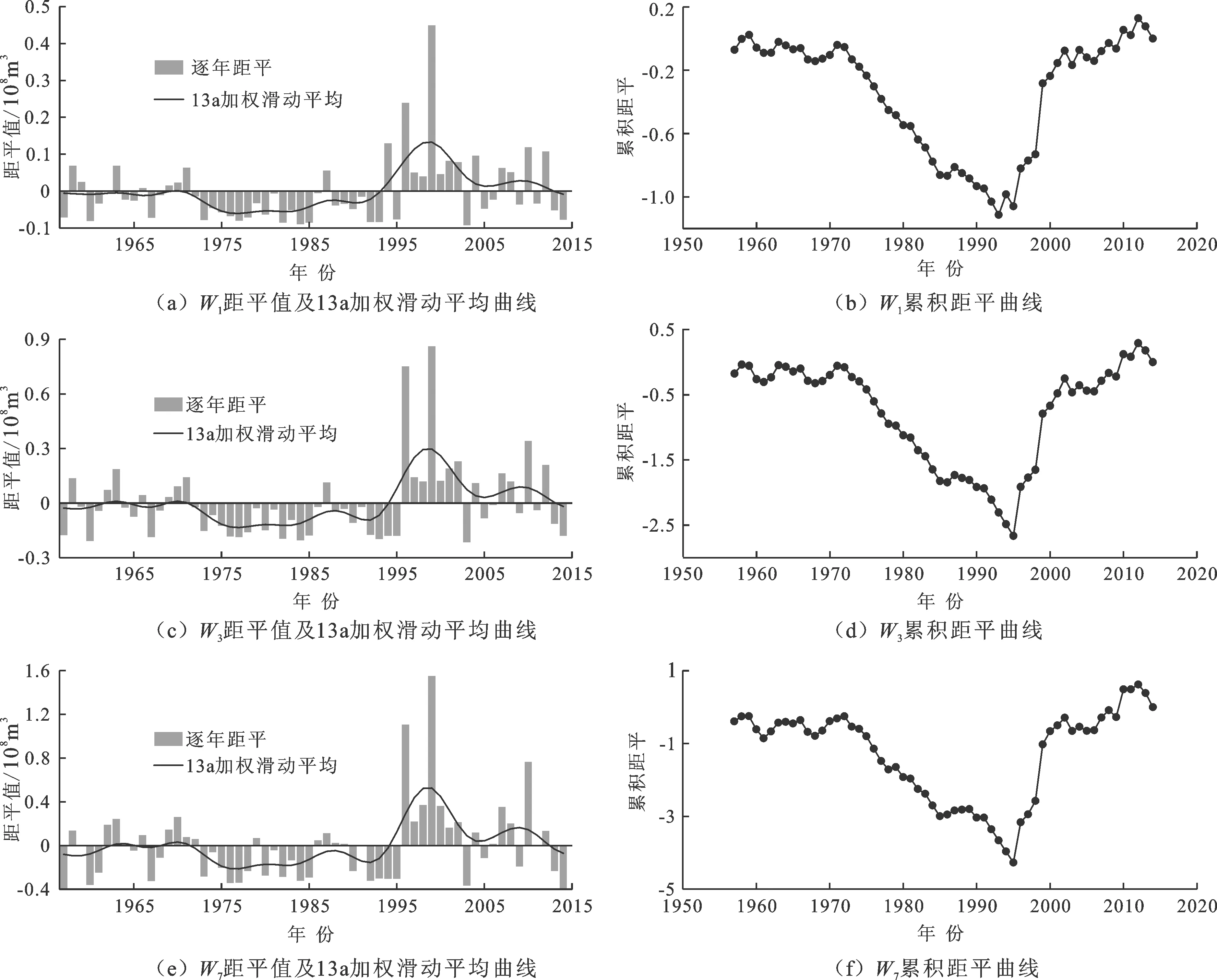
图2 1957-2014年玛纳斯河肯斯瓦特控制流域W1、W3、W7距平变化

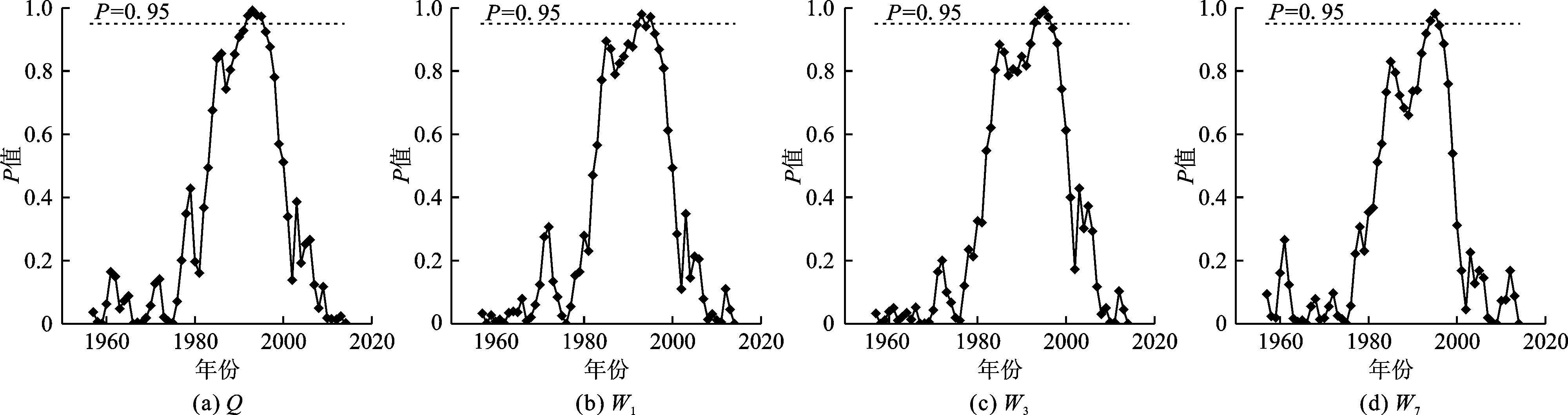
图3 1957-2014年玛纳斯河肯斯瓦特控制流域洪水特征序列Pettitt变异点检验

为了进一步检验突变点的位置，采用Lee-Heghinian法。由f(t)值的趋势变化，得到的结果如图4所示，分割点f值所对应的年份与Pettitt统计检验方法相同。从图4中可以看出Q序列和W1序列均在1993年与1995年出现峰值，而W3、W7在1995年出现峰值。由于全球气候变暖特征越发显著，IPCC第5次评估报告显示在1980-2012年间全球气温升高了0.85℃[15]。而对于受冰川补给影响的玛纳斯河，1996-2014年流域气温较1956-1995年气温均值增加2.13℃，使得流域冰川总储蓄量减小[16-18]。因此，气温变化对玛纳斯河流域序列变化产生了重要影响，结合两种突变点检验结果，最终确定峰量序列的变异点发生在1995年，这与累积距平法所得出的变异点一致。

选用R/S分析的赫斯特指数(H)及分数布朗运动相关函数[19]判断序列变异程度，见表2。其H值均大于0.5，结合相关函数C(t)可知，洪水各序列均存在中变异，但W1达到了强变异。

表2 水文序列变异程度分析表

4.3 阶段变化趋势性分析

由于环境的变化导致了玛纳斯河流域已不满足一致性要求，则以变异点为节点将时间序列分为前后两个阶段，即1957-1995年和1996-2014年。

1957-1995年Q的距平时间序列如图5(a)所示，距平值在此阶段总体上较为平稳，但中间有所波动，其最大距平值发生在1966年，但从距平值的滑动平均曲线可以看出此阶段总体呈下降趋势。1996-2014年Q距平时间序列由图5(b)所示，此阶段相对于上一阶段增幅为33.65%，但从2002年以后仅有两年出现正距平值，且数值均偏小。从距平值的滑动平均曲线可已看出，1998-2004年Q有较为明显的下降趋势，但2004年以来洪峰虽有下降但趋势并不明显。

图4 1957-2014年玛纳斯河肯斯瓦特控制流域洪水特征序列Lee-Heghinian变异点检验

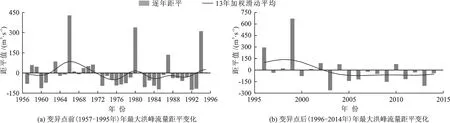
图5 1957-2014年年最大洪峰流量阶段性距平变化

图6为玛纳斯河流域1957-2014年两个阶段年最大1、3、7 d洪量距平值的趋势变化。图6表明，后一阶段的流量距平值明显大于前一阶段，其增幅分别为40.22%、39.14%、30.54%。可见近年来玛河的流量值发生了巨大的变化，且在前一阶段年最大洪量距平值均有较大的变化幅度，而后一阶段均出现了下降的趋势。

滑动平均曲线表明：可将前一阶段分为4个变化过程，1957-1970年流量较为平稳，且滑动平均曲线在坐标上方浮动；1971-1976年出现了明显的下降趋势；1977-1987年开始上升，其中1983年以前上升较为缓慢，而后曲线有较为明显的上升趋势；从1988年又出现了明显的下降趋势。后一阶段较前一阶段总体上波动幅度较小，以1998-2004年为下降趋势，之后下降趋于平缓。

根据M-K法分别对峰量1957-1995年与1996-2014年进行定量趋势分析，结果见表3。由表3可看出，其变异点后序列统计量U值均为负值，且绝对值总体小于1.96，则变异点后峰量两子序列均表现下降趋势，其中W3与W7在变异点后出现了显著性下降趋势。

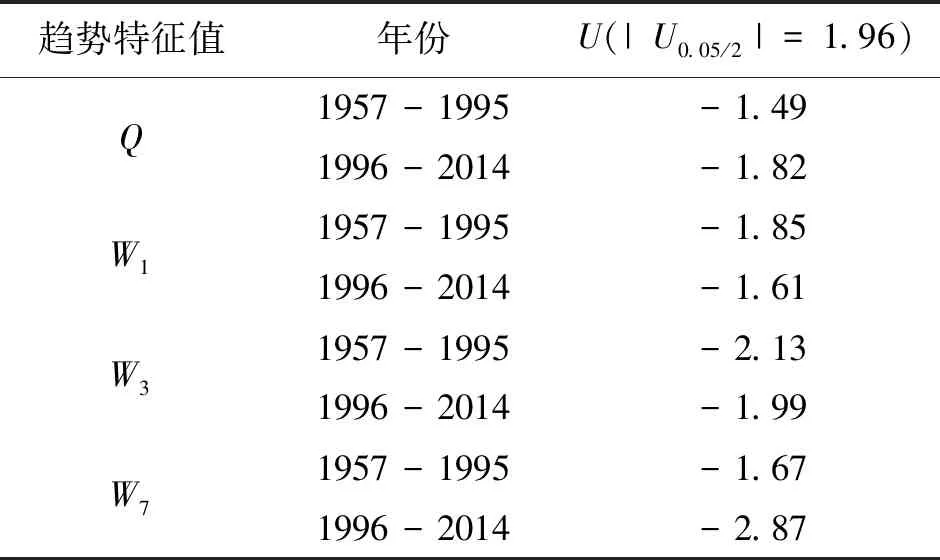
表3 变异点前后M-K统计值

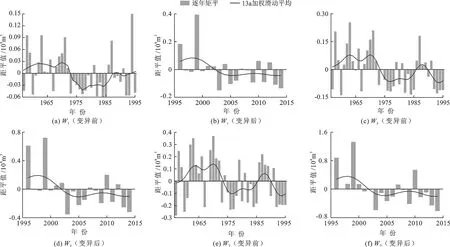
图6 1957-2014年玛纳斯河肯斯瓦特控制流域W1、W3、W7距平阶段性变化

5 结 论

根据玛纳斯河流域出山口肯斯瓦特水文站1957-2014年逐日径流资料，采用Pettitt法、Lee-Heghinian、加权滑动平均法、R/S法、M-K趋势检验法对玛纳斯河流域上游融雪洪水演变规律进行研究，结果表明：

(1)对玛纳斯河肯斯瓦特控制流域1957-2014年洪水序列进行滑动分析并通过累积距平曲线及M-K趋势定量分析，发现了峰量序列前后存在较大的差异，从而指出了由于气候变化和人类活动的影响，水文序列的一致性遭到了破坏，传统的水文序列已经不满足水文研究的内在要求。

(2)本文有效地利用R/S法和分数布朗运动分析了水文时间序列的变异程度。对于玛纳斯河流域峰量序列均呈现中等变异，其中年最大1 d洪量发生了强变异。

(3)鉴于融雪洪水特征序列年限长度的限制，以及在相关检验概率P值最大的情况下，选取1995年为洪峰、洪量最可能发生变异的年份，其变异点后峰量平均增长幅度为35.89%。在1957-1995年间，洪峰洪量各子序列均产生了较大的波动，而1996-2014年洪水序列呈现下降趋势。