天然白桦林立木材积估算研究

陈清华 ， 邓必平

(1.赣州市林业科学研究所，江西 赣州 341000；2. 江西环境工程职业学院，江西 赣州 341000)

1 引言

白桦林是大、小兴安岭地区分布范围较广，所占比重较大的森林类型，而在内蒙古自治区，白桦更是占阔叶树总面积的40%以上，占总蓄积量的60%以上。随着木材加工工业的发展，加上白桦材质均匀、材色洁白的优点，所以其用途及前景非常广泛，不但可以做胶合板、木地板、纸浆材、卫生筷，还可以用做工艺材，制作家具，而且几乎是航空胶合板的不可替代的树种。白桦用途之广泛，价值之昂贵，再加上白桦林已遭到严重的人为破坏，致使白桦资源受到越来越多的重视。而为了满足国民经济的发展和由于人民生活水平的提高而对木质材料的需求，所以科学地经营和管理好现有的白桦林，提高白桦林的生长与收益是当前大、小兴安岭地区林业生产中的一项急待解决的问题，而且编制白桦的立木材积表是准确计量林分蓄积量的依据，对生产实践都有很好的指导作用。

2 标准木资料的调查收集

2.1 研究地区概况

研究地位于小兴安岭山脉，山文方向近似为西北，山势低缓，海拔为600～1000 m。分水岭两侧不对称，西南坡较缓长，而东北坡陡短。地貌相比差异显著，北坡陡峭，成阶梯状，水系短促，多台地、宽谷；中部低山丘陵，山势和缓；南坡山势浑圆平缓，水系绵长，属低山，山势较陡。最高峰为平顶山，海拔1429 m。西部铁力市位于松嫩平原，地势呈波状。 总面积13万 km2，其中低山约占37%、丘陵约占53%、浅丘台地约占10%。海拔500～800 m。在诸多自然因素的综合作用下，这里的土壤主要为暗棕壤，此外还有草甸土和沼泽土，部分高山地带为山地棕色针叶林土。

小兴安岭属北温带大陆季风气候区，受太平洋季风与西伯利亚高寒气旋双重影响。四季分明，冬季漫长严寒，最低气温达-43 ℃，少风多雪，积雪深度常达30～80 cm，；春季回暖快；夏季温热湿润；秋季暂短、降温迅速。年平均气温为-1～1 ℃，最冷月为1月份，气温为-25～-20 ℃，最热月为7月份，气温为20～21 ℃，极端最高气温为35 ℃。全年≥10 ℃活动积温1800～2400 ℃，无霜期为90～120 d。年平均日照数2355～2400 h。年降雨量550～670 mm，降雨集中在夏季。干湿指数1.13～0.92，属湿润地区。

2.2 资料收集和整理

本文所用资料取自2011年黑龙江省五营林业局调查的平均木解析木资料。五营林业局位于黑龙江省伊春市北部，小兴安岭南坡腹部，五营区盛产红松，素有“红松故乡”之美誉，是黑龙江省唯一的森林生态旅游示范区。现行政企合一管理体制，行政区划面积1470 km2，总人口4.5万人，森林总蓄积685.1万m3，森林覆盖率89.2%，年产木材4.5万m3。

3 材积表的编制

3.1 一元材积表的编制

3.1.1 散点图的绘制与模型的比较

利用胸径和材积(表1)绘制出散点图(图1)，通过散点图可以帮助选择模型，从散点图可以看出胸径和材积两者之间的关系为曲线图，根据经验有以下9种模型可供选择：

QUA:v=b0+b1d+b2d2

(1)

COM:v=b0(b1d)orlnv=lnb0+lnb1d

(2)

GRO:v=exp(b0+b1d)orlnv=b0+(b1d)

(3)

LOG:v=b0+(b1lnd)

(4)

CUB:v=b0+b1d+b2d2+b3d3

(5)

S:v=exp(b0+b1/d)orlny=b0+(b1/d)

(6)

EXP:v=b0[exp(b1d)]orlnv=lnb0+b1d

(7)

INV:v=b0+(b1/d)

(8)

POW:v=b0db1orlnv=lnb0+(b1lnd)

(9)

表1 小兴安岭南坡白桦的树高、胸径、材积生长过程

注：引自《黑龙江森林》

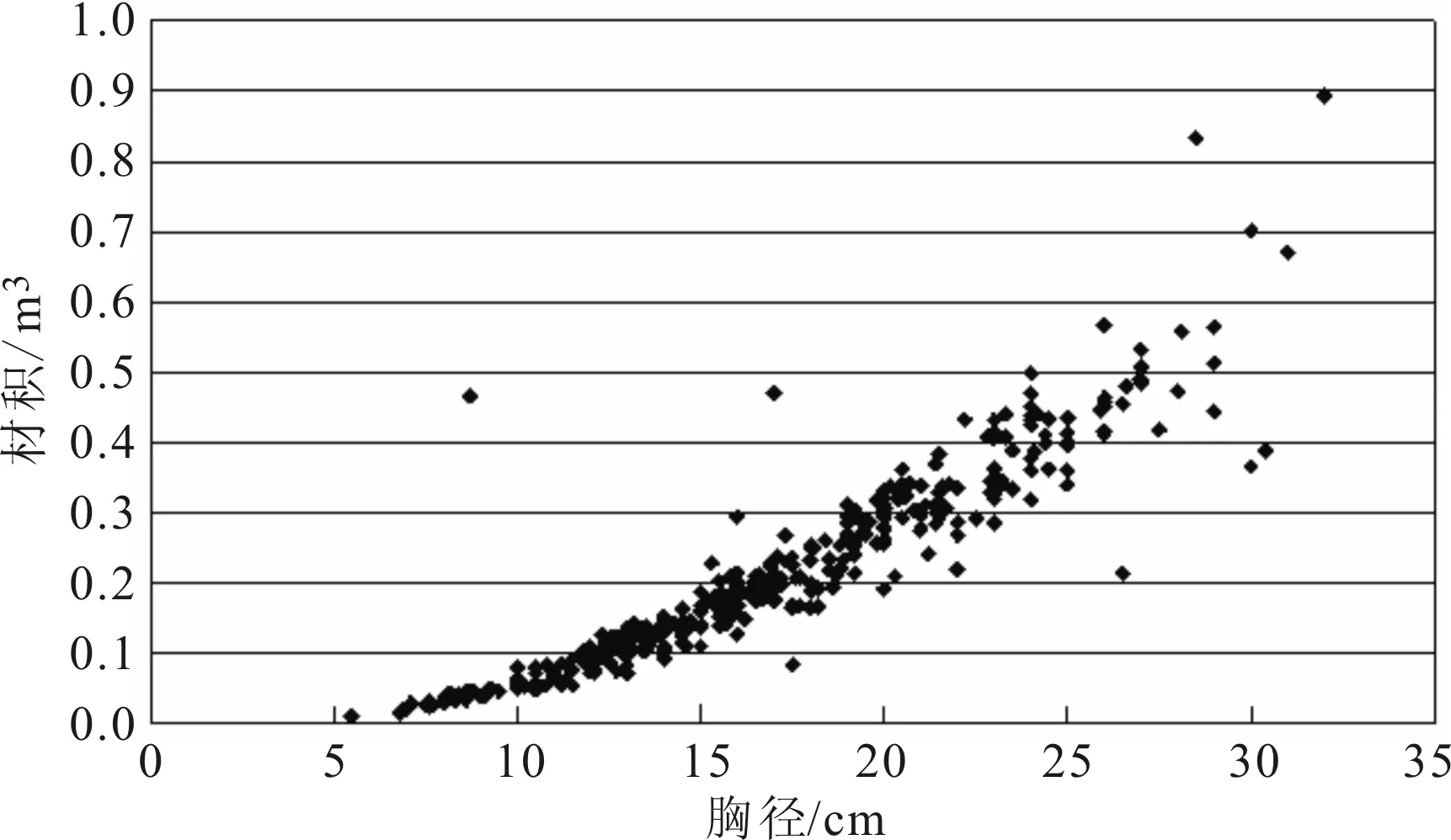
图1 胸径与材积关系散点

3.1.2 模型的计算

利用SAS软件进行曲线回归所得结果见表2。

另有两个非线性模型采用非线性回归的方法所得参数如下。

(1)布里那克(bulinnake)一元回归方程：

利用SAS软件求得方程系数：b0= -5.05106,b1=1.427829,b2=-10.1201

相关系数：R=0.9389

(2)卢则(luze)一元材积回归方程：v=a[d3/(1+d)]

利用SAS软件求得方程系数：a=0.000711,相关系数：R = 0.93755

表2 各模型回归系数

选择模型的一般原则是选出相关系数最大的模型方程。综上，通过相关系数比较可得知方程CUB:v=b0+b1d+b2d2+b3d3的相关系数最大，所以该方程为最佳模型，代入参数可得CUB统计模型:v=-0.00888+(-0.00143d)+0.000942d2+(-0.00000771d3)

利用该数学模型进行编制一元材积表。

以上各模型的统计回归图与样本散点图的关系见图2。

从图2可以看出回归得出的曲线中CUB统计模型和用实测值绘制的散点图最接近，说明拟合效果最好，可用该数学模型编制一元材积表。此外，QUA统计模型、POW统计模型、S统计模型和用实测值绘制的散点图也比较接近，效果也比较好。而INV统计模型、LOG统计模型、EXP统计模型、GRO统计模型、COM统计模型则与用实测值绘制的散点图相差较大，拟合效果差，所以不能选用它们编制一元材积表。

3.2 二元材积表的编制

二元立木材积表是按照立木的胸径D和树高H两个测树因子编制的立林材积表。本文采用了10种数学模型用以描述材积与胸径和树高的关系。

3.2.1 模型的比较

以下列出可供选择的10种数学模型，根据经验方程可分别计算出相关系数值以进行比较，可初步选出相关系数最大的方程为最佳模型。

V1:v=a+bD+cD2+dDH+eD2H+fG

(10)

V2:v=a+bD+cD2+dDH+eD2H

(11)

V3:v=a+bD2+cD2H+dH+eD2H+fG

(12)

V4:v=a+bD2+cD2H+dH

(13)

V5:v=a+cD2H+dH2+eDH2

(14)

V6:v=a+bD2H

(15)

V7:v=a(D2H)b

(16)

V8:v=D2(a+bH)

(17)

V9:v=aDbHc

(18)

V10:v=D2H/(a+bD)

(19)

3.2.2 模型的计算

利用SAS软件进行曲线回归所得结果见表3。

图2 统计回归与样本的关系

表3 各模型回归系

通过比较得知方程 V5：

v=a+cD2H+dH2+eDH2：的相关系数R最大，所以初选模型V5为最优模型。利用软件SAS计算出各系数如下：

a=0.044852 c = 0.000011

d = -0.00039 e =0.000039

求得方程为:

v=0.044852+0.000011D2H+(-0.00039H2)+0.000039DH2

(20)

再利用残差图对各模型进行分析检验，以上各模型与样本的材积残差图见图3。

从以上各残差图可以看出各模型的残差都呈均匀的带状分布，并且97.5%的残差都落在-0.1～0.1之间，所以选用的数学模型的精度是可靠的，再结合相关系数，可以确定选择V5数学模型来编制二元材积表。

4 结论

根据经验列出9个一元材积方程候选数学模型，并利用SAS软件进行相关系数的计算和分析，经过比较选出相关系数R值最大的数学模型CUB为最优模型。

用独立样本对材积式进行差异显著性分析，通过各数学模型的统计回归图与样本散点图的比较，确定出数学模型的精度，并选出拟合度最好的数学模型CUB。

图3 各模型与样本的材积残差图

根据经验列出10个二元材积方程候选数学模型，并利用SAS软件进行相关系数的计算和分析，经过比较选出相关系数R值最大的数学模型V5为最优模型。

用独立样本对材积式进行差异显著性分析，通过各数学模型与实测样本的材积残差图的分析，确定出数学模型的精度，并选择出最好的数学模型V5。

利用选出的一元、二元材积方程分别编制出小兴安岭地区白桦林的一元、二元立木材积表。

5 讨论

由于标准木的调查工作量较大，受样本数量及测量误差和记录误差的影响，对材积表数学模型的拟合精度有一定的影响。

本研究所选择出的用于编制一元、二元材积表的数学模型经过了精度检验，所以所编制的材积表也是有相当高的可靠度的，可以为以后的生产实践提供理论依据。

对于白桦林的经营，既要保证在条件允许的情况下，尽可能的恢复较稳定、生产力较高的针叶林或针阔叶混交林，又要因地制宜地采取合理措施，培育好现有的白桦林。