高强钢筋约束超高性能混凝土柱轴心受压本构模型研究

邓宗才，姚军锁

(北京工业大学城市与工程安全减灾省部共建教育部重点实验室，北京 100124)

超高性能混凝土(ultra high performance concrete，UHPC)是一种高韧性、高耐久性、高强度的新型超高性能水泥基复合材料[1]，其为高强钢筋的应用提供了有利条件，两种高强材料优势互补[2－3]，可形成高强、高变形性能的钢-UHPC体系，有利于满足现代结构对功能和可靠性的要求。

100 多年来国内外约束混凝土研究的成果丰硕[4]，建立了 Kent-Park 模型[5]、Sheikh 模型[6]、Mander模型[7]、过镇海模型[8]、Cusson-Paultre模型[9]、Razvi-Saatcioglu模型[10]等经典约束模型，研究对象也逐步趋于高强、高性能化。对约束UHPC的研究，Sugano等[11]对700 MPa~1400 MPa的高强箍筋约束UHPC柱进行轴压试验，证实了高强箍筋可有效约束UHPC，给出了高强箍筋约束UHPC峰值应力、应变计算式，但未考虑峰值应力时高强箍筋是否屈服。Empelmann等[12－14]研究了配置高强纵筋的UHPC方柱受压性能，认为在适量箍筋约束下钢纤维和高强纵筋组合可显著提高构件轴压性能，证实了文献[15]的本构方程能较好预测约束 UHPC本构上升段。Hosinieh等[16]进行了 Razvi-Saatcioglu模型[10]、Légeron-Paultre模型[17]与 Aoude模型[18]对约束UHPC适用性的研究，证实三种模型均不能较好地适用于约束 UHPC。Yang等[19]研究了无纵筋的约束UHPC圆柱的应力-应变特性，探讨了Mander模型[7]及 Razvi-Saatcioglu模型[10]对约束 UHPC的适用性，得出前者可准确预测约束UHPC峰前响应但会高估峰后特性，而后者会低估约束UHPC的整体性能。Shin等[20－21]先后研究了含混杂纤维的UHPC轴压方柱和圆柱的约束效应，并在 Cusson-Paultre模型[9]的基础上提出了修正的约束UHPC本构模型。

目前对高强箍筋约束UHPC的研究刚刚起步，对约束UHPC本构模型的研究鲜有报道。为此，本文在HTRB630新型高强箍筋约束UHPC柱轴压试验的基础上，建立了约束UHPC的本构模型，包括受压应力-应变关系、峰值应力及应变的计算方法等，为UHPC结构设计和非线性理论分析提供参考。

1 试验研究

1.1 试件设计及加载制度

为研究箍筋约束 UHPC应力-应变本构关系，以箍筋强度、箍筋形式及体积配箍率为主要参量，对9根箍筋约束UHPC柱进行了轴压试验，其中5根高强箍筋柱、4根普通箍筋柱，尺寸均为230 mm×230 mm×700 mm。纵筋均配置8根直径16 mm的HRB400E级钢筋，屈服强度为470 MPa。箍筋采用HRB400、HTRB630级钢筋，其拉伸试验应力-位移曲线见图1。钢筋本构均采用理想弹塑性模型[8,22]；箍筋间距取60 mm、80 mm；箍筋形式采用矩形箍筋(R)、菱形复合箍筋(L)、菱形十字复合箍筋(C)(如图2(a)所示)。体积配箍率ρv为 2.1%~4.7%。图3为钢筋笼绑扎实物图。

图1 钢筋拉伸试验应力-位移曲线Fig.1 Tension test results of steel reinforcement

图2 试件设计、加载装置及测点布置图 /mmFig.2 Column design details,test machine and measuring points

图3 钢筋笼绑扎实物图Fig.3 Reinforcing cage

试件设计参数详见表1，其中试件编号H代表高强箍筋HTRB630，N代表普通箍筋HRB400，如：HL-1，“HL”代表菱形复合高强箍筋 UHPC柱，“-1”仅作编号以区分同种箍筋形式不同配箍率的试件。

试验所用 UHPC内掺直径 0.2 mm、长度13 mm、抗拉强度2800 MPa的平直形镀铜钢纤维，所有柱均竖向浇筑成型，拆模后 90 ℃蒸汽养护48 h，后在室温条件下养护至试验。浇筑时每批预留3个边长100 mm的立方体试块，试验测得立方体抗压强度fcu见表1。此外，试验设计了与配筋柱同尺寸的未配筋UHPC柱P，所测未约束UHPC峰值强度fc0为100.37 MPa，应力-应变曲线见图4。

试件在 20000 kN电液伺服压力试验机上进行单调静力加载，为防止端部提前破坏，加载前在柱两端夹设宽100 mm、厚8 mm的钢箍，见图2(b)试验加载装置图。试验加载首先采用荷载控制，加载速率为3 kN/s；当加载至预估峰值荷载的 80%左右改用位移控制，加载速率改为0.0033 mm/s，缓慢连续加载至承载力下降到峰值荷载的50%或总竖向位移达到30 mm，视为试件破坏，停止加载。

试件应变片及测点布置见图2。箍筋约束UHPC柱轴压试验结果见表1，表中：d为箍筋直径；s为箍筋间距；fyv为箍筋屈服强度；εc0为未约束UHPC峰值应变[23]；fcc、εcc分别为约束UHPC的峰值应力、应变；ε85、ε60分别为约束UHPC峰值应力下降15%及40%时所对应的轴向应变；εcc,sv为约束UHPC峰值应力时内外箍筋应变实测值的平均值。

表1 试件设计参数及试验结果Table 1 Column design parameters and test results

1.2 约束UHPC的应力-应变全曲线

图4、图5分别为普通箍筋、高强箍筋约束UHPC应力-应变全曲线，其纵坐标为核心区约束UHPC名义轴向压应力，横坐标为约束UHPC的轴向应变(取每侧两个位移计读数差值的平均值与标距400 mm之比)。由图4和图5可知，体积配箍率越大(尤其是ρv=3.5%~4.7%)，下降段越趋平缓，核心UHPC的强度及变形能力越高，说明增加配箍率是防止应力-应变曲线陡降的有效措施。

对仅由箍筋间距或箍筋形式引起的ρv变化，箍筋间距越小(如HL-1与HL-2、NL-1与NL-2)、箍筋形式越复杂(如HR、HL-2及HC，NR、NL-2及 NC)，约束UHPC的强度及变形能力改善越显著。原因是箍筋间距和形式均决定着相邻箍筋所约束的核心UHPC的有效体积[24－25]，箍筋间距决定着约束应力沿试件纵向的均匀度，减小箍距可以削弱“拱作用效应”[6－7]，使相邻箍筋中间控制截面上的有效约束面积及应力增大，箍筋约束应力沿试件纵向传递更均匀，整体约束作用增强；箍筋形式决定着约束应力在试件截面上的均匀度，复合箍筋可有效减少弱约束区面积，从而提高对UHPC的约束效果。

对比图4和图5可知，高强箍筋试件峰值点后均有所陡降，后趋于平稳，且残余承载力较高，是因为 UHPC保护层在峰后逐渐退出工作，核心UHPC变形增大，承载力下降明显，而后由于核心UHPC的变形充分激发了高强箍筋的约束应力，使核心UHPC三向受压明显，强度下降相对缓慢，且高强箍筋高约束应力的分力及裂缝面上钢纤维的黏聚阻力承担了轴向力沿斜裂缝的滑动分力，使高强箍筋试件具有较高的残余承载力。配箍率3.5%~4.7%的高强箍筋试件的强度均比同配箍率普通箍筋试件有显著提高，下降段平缓，残余承载力较高。表明UHPC宜采用高强箍筋进行约束，其适配性较好，高强箍筋对提高约束UHPC强度及变形能力优于普通箍筋。由图5可知，高体积率、小间距且箍筋形式复杂的高强箍筋约束UHPC具有较为理想的轴压性能，如HL-1、HC。

图4 普通箍筋约束UHPC轴压应力-应变全曲线Fig.4 Stress-strain curves of confined UHPC with normal-strength stirrups

图5 高强箍筋约束UHPC轴压应力-应变全曲线Fig.5 Stress-strain curves of confined UHPC with high-strength stirrups

2 约束UHPC理论分析

2.1 箍筋有效约束应力

核心区约束 UHPC在轴压作用下产生横向变形，使箍筋直线段受弯拉作用，但由于直线段箍筋抗弯刚度较小，所产生的侧向约束反力较弱，而刚度较大的转角处箍筋产生的约束反力较强[8,26]。因此，如图6(b)中截面2-2所示，箍筋提供的侧向约束力在核心UHPC四周呈不均匀分布，箍筋平面内的核心UHPC可分为强、弱约束区；考虑到箍筋的“拱作用效应”[6－7]，如图6(a)所示，各截面上的强约束区面积沿试件纵向是变化的，相邻箍筋的中间截面(即控制截面)最小，箍筋平面内最大(见图6(b)中截面2-2)。

图6 有效约束核心区UHPC及受力分析Fig.6 Effectively confined core UHPC and force analysis

为简化计算，假设箍筋提供的侧向约束力沿核心UHPC四周均匀分布，且纵向各截面所受约束应力相等，故对箍筋及核心UHPC的隔离体进行受力分析，见图6(b)，得到平均侧向约束应力σl，见式(1)。而试件极限承载力取决于控制截面，该截面的有效约束面积与纵筋布置、截面尺寸、箍筋形式及间距等因素有关，且小于箍筋平面内核心UHPC面积，为此引入Mander等[7]提出的有效约束系数ke。联立式(1)~式(3)求得箍筋对控制截面的有效侧向约束应力计算式(4)。

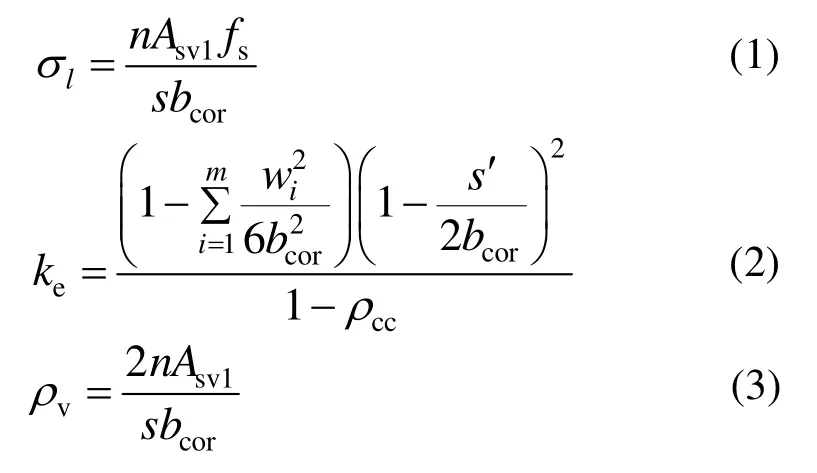
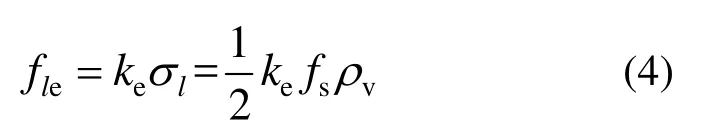
式中：fle为有效侧向约束应力；fs为约束UHPC峰值应力时的箍筋应力；s＇为相邻箍筋净距；wi为相邻纵筋净距；bcor为箍筋中心线间的核心UHPC宽度；Asv1为单肢箍筋的面积；m为纵筋根数；n为箍筋肢数，对R形、L形、C形箍筋n分别取2.00、3.41、4.41；ρcc为核心区配筋率。

2.2 高强箍筋应力取值

图7为部分典型试件的箍筋应变随约束UHPC轴向应力变化的曲线。外部箍筋比内部箍筋应变发展较快；高配箍率试件(HL-1、NL-1)在峰值应力时箍筋应变较大，低配箍率试件(HL-3、NR)的箍筋应变较小，且高配箍率的箍筋破坏多呈屈服破坏且颈缩明显，低配箍率的箍筋破坏时仅绑丝节点被拉开(见图8)，说明配箍率越高其约束作用发挥越充分，对试件强度的提高越明显；在约束UHPC峰值应力附近，普通箍筋一般均达到屈服强度，而高强箍筋大多在峰后屈服，说明高强箍筋在峰值后的富余量可提高柱的安全储备，增强抗震延性，提高残余承载力。

图7 箍筋微应变与轴向应力曲线Fig.7 Stress-microstrain curves of stirrups

图8 箍筋屈服破坏情况Fig.8 The yield failure of stirrup

在计算约束UHPC峰值点所对应的箍筋约束应力时，普通箍筋可取屈服强度，高强箍筋必须取其实际应力而不能直接采用屈服强度，否则会高估高强箍筋的应力发挥。故将各高强箍筋试件峰值应力时内外高强箍筋实测应变平均值εcc,sv列于表1。

研究表明[27－28]，影响箍筋应力发挥的因素主要有体积配箍率、混凝土强度、截面尺寸、箍筋间距、箍筋形式及屈服强度等。故假设约束UHPC峰值点处的高强箍筋应力是以上因素的函数，引入有效约束系数ke和配箍特征值λv，用约束指标Ie统一表达。根据数据拟合出约束UHPC峰值点处的高强箍筋应力fs计算式(5)，计算值与试验值的对比见图9，平均值为1.0，变异系数为1.69%。

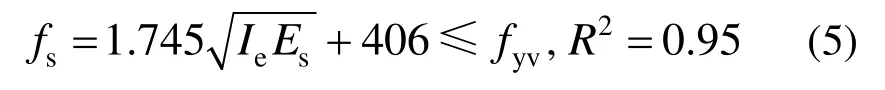
式中：Ie为有效约束指标，Ie=0.5keλv；λv=ρvfyv/fc0为配箍特征值，其中fyv为高强箍筋屈服强度；Es为箍筋的弹性模量，取200 GPa。该公式仅适用于屈服强度为700 MPa的高强钢筋应力计算。

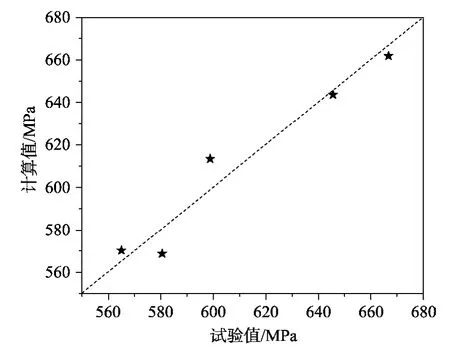
图9 箍筋应力计算值与试验值的对比Fig.9 Ratio of calculated value of the stirrup stress to experimental value

2.3 峰值应力、应变计算

核心UHPC在侧向约束作用下处于三轴受压复杂应力状态，破坏机制与单轴受压破坏有差异。因此在求核心区约束UHPC的峰值应力时，采用精确度高、适用范围广且合理性强的 Ottosen混凝土破坏准则[8,29]，并用相对八面体强度来统一表达[30]，见式(10)。其中，令f1=f2=-fle，f3=-fcc代入相对八面体强度表达式(6)和式(7)，联立式(6)~式(8)化简得式(9)。

式中：σoct、τoct分别为八面体正应力和切应力；σ0、τ0分别为相对八面体正应力和切应力；f1、f2、f3为三个方向的主应力；a、b、λ均为与试验相关的待拟合系数。

根据试验数据拟合出fcc计算式(10)，拟合度R2=0.93，见图10；拟合出拟合度R2=0.90的εcc计算式(11)，见图11。此外，在下降段0.6倍的峰值应力点，箍筋基本均已屈服，故在拟合ε60的计算式时，箍筋应力均取屈服强度，并用Ie进行表达，拟合出ε60计算式(12)，拟合度R2=0.95，见图12。式(10)~式(12)适用于屈服强度700 MPa的高强箍筋约束、立方体抗压强度约为150 MPa的UHPC轴压短柱。

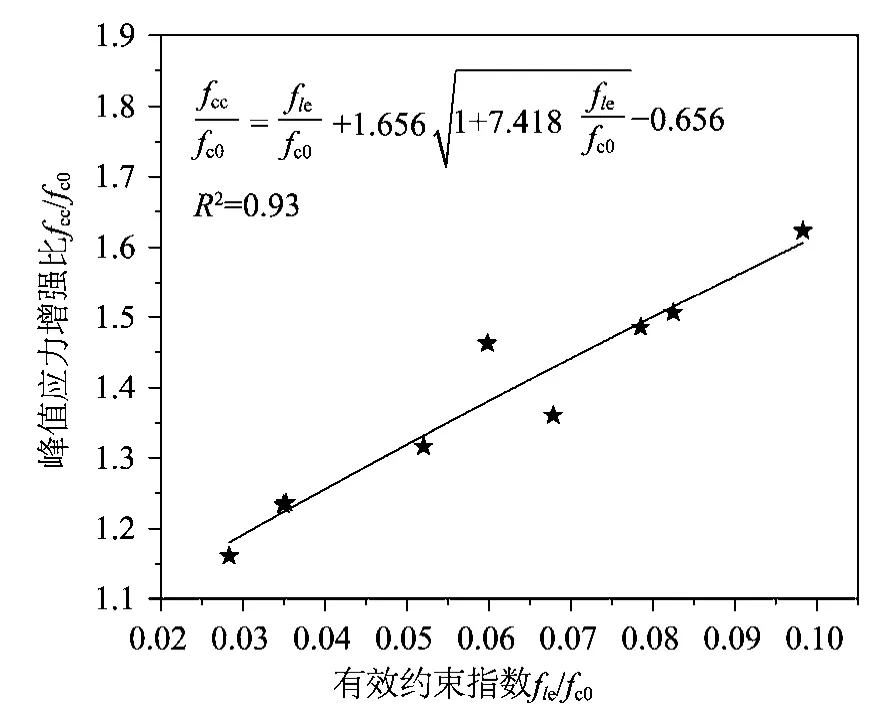
图10 fcc/fc0-fle/fc0关系曲线Fig.10 Relationship between fcc/fc0 and fle/fc0

图11 εcc/εc0-fle/fc0关系曲线Fig.11 Relationship between εcc/εc0 and fle/fc0

图12 ε60/εc0-Ie关系曲线Fig.12 Relationship between ε60/εc0 and Ie

3 约束UHPC本构模型

3.1 本构模型建立

建立约束UHPC本构模型是进行UHPC结构设计和非线性分析的基础，对分析约束UHPC柱的承载力及变形性能具有重要作用。本文以规范[22]中的混凝土单轴受压本构表达式为基础，建立两段式约束UHPC本构模型。

式(13)为含参数a的有理分式上升段，参数a可控制上升段初始刚度，为方便本文的约束UHPC本构与文献[23]的未约束UHPC本构上升段能相互转化，考虑了文献[23]提供的未约束UHPC本构上升段参数A(计算式见文献[23])，即无约束时式(14)中a等于A。Ie越大，参数a越大，曲线初始刚度越大，上升段中的弹性段占比减小，反之初始刚度越小、弹性段占比增加。是因为高约束试件在高约束应力作用下，整体抗损稳定性提高，使之在峰值前具有较大的塑性变形，而低约束试件出现塑性变形之后，并不能提供较高的约束应力来分担轴压荷载，致使产生较小的塑性变形即达到极限承载力。上升段：

式(15)为含参数αc、k的有理分式下降段，是在规范[22]的基础上引入控制下降段凹凸度的参数k来考虑箍筋约束影响，而控制下降段坡度的参数αc可以根据下降段边界条件确定：曲线过点(ε60，0.6fcc)，将此点代入式(15)使得αc可用k来表达，见式(16)。Ie越大，参数k越大，下降段越趋平缓，反之下降段陡降且凹陷状明显。

下降段：

3.2 本构模型对比

图13为采用Mander模型(M)[7]、Cusson-Paultre模型(C-P)[9]、Aoude模型(A)[16,18]及本文约束UHPC模型计算得到的应力-应变曲线与试验曲线的对比。

结果表明，上述典型模型的弹性上升段与试验曲线较吻合，但由于高致密、高强的纤维增强UHPC具有较长的弹性段，使传统模型的弹塑性上升段与试验曲线吻合度变差。此外，传统模型的峰值点及下降段与试验曲线差异较大；本文模型的计算曲线与试验曲线吻合良好。

Mander模型是普通箍筋约束混凝土模型，其峰值点及下降段偏高(尤其是高强箍筋试件)，高估了约束UHPC的轴压性能，是因为该模型未考虑峰值时箍筋是否屈服，直接用屈服强度进行计算，适合普通箍筋，但高估了高强箍筋的应力发挥。Aoude模型是约束纤维混凝土(FRC)模型，其上升段及峰值应变预测较好，但强度及下降段比试验曲线较高，是因为该模型认为箍筋与异型钢纤维在改善约束混凝土峰后性能方面具有混合增强增韧效应，峰值应力及下降段额外考虑了异型钢纤维的约束提高作用。Cusson-Paultre模型是约束高强混凝土(HSC)模型，其峰值应变预测较好，对Ie≤0.068的试件峰值点预测较准确，是因为该模型是在大量的试验数据基础上建立的，适用范围广；但低估了约束UHPC的下降段性能，是因为UHPC和HSC显著不同：UHPC属于纤维增强水泥基复合材料，钢纤维的增韧阻裂效应，使其具有应变硬化和多裂缝扩展特性，脆性明显降低，韧性显著增加；下降段核心UHPC完整性较好，配箍量、未屈服箍筋的富余量及钢纤维的黏聚阻力等诸多因素综合作用，使约束UHPC下降段平缓、延性及耗能能力相对脆性大的HSC较好，残余承载力较高。

图13 各模型应力-应变曲线的对比图Fig.13 Comparison of stress-strain models

4 结论

通过对9根箍筋约束UHPC试件应力-应变关系的分析，得出以下结论：

(1)UHPC宜采用高强箍筋进行约束且适配性较好，高强箍筋可提供较高的约束应力，其在提高约束 UHPC的强度及变形能力方面均优于普通箍筋，可形成高强、高变形性能的钢-UHPC体系。

(2)增加配箍率是防止应力-应变曲线陡降的有效措施；采用高体积率、小间距且形式复杂的高强箍筋约束UHPC，可显著提高试件强度及变形能力，且残余承载力较高。

(3)高强箍筋大多在约束UHPC峰值后屈服，其富余量可提高柱的安全储备，增强抗震延性。故计算约束UHPC峰值点时，普通箍筋可取屈服强度，而高强箍筋实际应力拟按式(5)计算，否则会高估其约束作用。

(4)建立了约束UHPC峰值应力、应变计算式及核心区约束UHPC本构模型，并与几种典型的约束混凝土模型对比，结果表明本文模型的理论计算结果与试验实测结果吻合度较高。但因本文试件数量及参数有限，仍需更全面的试验数据作支撑来提高本文公式的适用性及精度。