基于贝叶斯MCMC方法的高斯烟羽模型不确定性分析

崔威杰 曹 博 陈义学

1（华北电力大学核科学与工程学院 北京102206）

2（华北电力大学非能动核能安全技术北京市重点实验室 北京102206）

当前核电厂采取了越来越好的安全设施，安全性已经达到了很高的水平，其中三代核电站AP1000发生大规模放射性物质泄漏事故的概率已被降低到1 × 10-8a-1［1］，但仍然不能就此不再考虑核电厂发生严重事故的可能性。一旦核电厂发生了放射性物质泄漏事故，放射性物质随大气的扩散将会造成快速、大范围的严重影响，因此必须及时评估放射性后果以制定合理的应对策略。这种情况下，由于风场、大气湍流、温度层结等的复杂性和难以准确监测的问题［2］，造成了气象观测资料的不确定性。此外，大气扩散模型中还存在由于对实际问题的简化而导致的不确定性。如果在事故后果评价时直接使用模型得到的确定性结果，则可能出现决策的失误［3］。因此需要采取合适的方法对大气扩散模型进行不确定性分析，降低决策失误的风险。

高斯烟羽模型是当前大气扩散模型中应用最为广泛的模型之一，其突出优点有输入参数少、所需计算资源少、比较符合观测情况等。2018年发布的环境影响评价技术导则（HJ 2.2-2018）［4］中，推荐了两种基于高斯烟羽模型的进一步预测模型——AERMOD［5］和 ADMS［6］。除此之外 ，美国开发的HotSpot［7］程 序 、欧 洲 开 发 的 ATSTEP［8］模 型 及Polyphemus系统［9］，以及广泛用于核电厂评审的ARCON96模型［10］和PAVAN程序［11］等都包含基于高斯烟羽模型的计算模块。本文利用基于高斯烟羽模型及其修正条件开发的大气扩散模拟程序进行了参数敏感性分析和不确定性分析。

1 高斯烟羽模型及其敏感性分析

1.1 理论模型

本文使用高斯烟羽模型作为计算模型，以连续点源释放引起的大气放射性浓度作为计算对象。该模型假设放射性污染物释放点在位于地面上的原点的正上方，下风向为x轴方向，y轴垂直于x轴，z轴由原点垂直向上。模型简化过程中采用了以下基本假设［12］：

1）污染物浓度在y轴、z轴方向上呈高斯分布（正态分布）；

2）风速是均匀稳定的，且大于1 m·s-1；

3）源强是均匀连续的点源；

4）湍流场是平稳均匀的；

5）弥散过程中污染物质量（或核素活度）是守恒的；

6）地面对烟羽具有完全反射作用。

基于以上假设，高斯烟羽模型的计算公式可以写成：

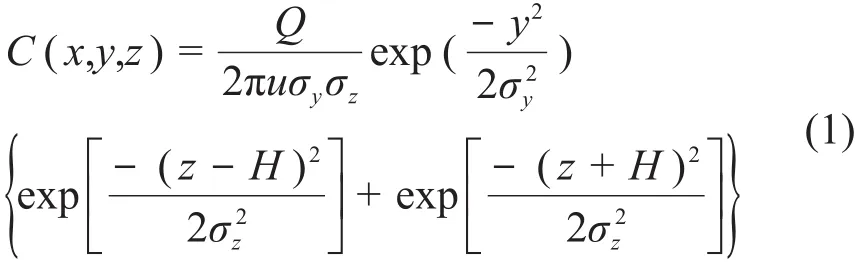
式中：Q是泄漏源强度，Bq·s-1；σy和σz分别为y方向和z方向上的高斯扩散系数，m；u为有效释放高度处的风速，m·s-1；H为有效释放高度，m。在上述方程的基础上，考虑可导致烟羽耗减的干沉积、湿沉积以及放射性核素衰变等的影响后，可以得到更符合现实情况的高斯烟羽模型。

1.2 参数敏感性分析

在进行模型参数不确定性分析之前，通常先进行参数敏感性分析，以找出对模型结果影响较大的几个参数，对这几个参数进行不确定性分析，可以在基本保证不确定性分析的准确性和可信度时，大大减少计算量。

参数敏感性分析的主要方法有一次一个变量法、标准回归系数法及Sobol敏感度指标等方法。一次一个变量法是每次变动一个参数，保持其余参数不变，统计运算结果的变动情况，进而得出模型结果对该参数的敏感性；标准回归系数法是用随机抽样方法产生输入参数样本，将其输入到模型中得到模型结果，进行最小二乘回归分析；Sobol敏感度指标按照参数对模型结果方差的贡献来划分敏感性等级［13］。

本文采用一次一个变量方法对5个重要输入参数（释放高度、10 m高度处风速（以下称参考风速）、烟羽释放半径、烟羽释放速率及烟羽温度）进行敏感性分析。首先确定各参数初始值，然后以初始值的20%为步长进行依次计算，记录每个参数变化过程中模型计算出的最大空气浓度值，最后分析每个参数变化引起的最大空气浓度标准差，标准差越大则表明模型对相应参数的敏感性越大［14］。源项假设为单核素137Cs释放，释放率为3.70×1010Bq·s-1，大气稳定度设置为D。分析过程如表1所示。

由表1中的数据计算得到释放高度、参考风速、释放半径、释放速率、烟羽温度依次对应的最大浓度标 准 差 依 次 为 1.09×105Bq·m-3、4.71×104Bq·m-3、2.17×104Bq·m-3、1.09×104Bq·m-3、8.56×103Bq·m-3，因此参数敏感性从大到小排序为：释放高度，参考风速，烟羽释放半径，烟羽释放速率，烟羽温度。模型对释放高度和参考风速具有最大的敏感性，故而选取这两个参数进行不确定性分析。

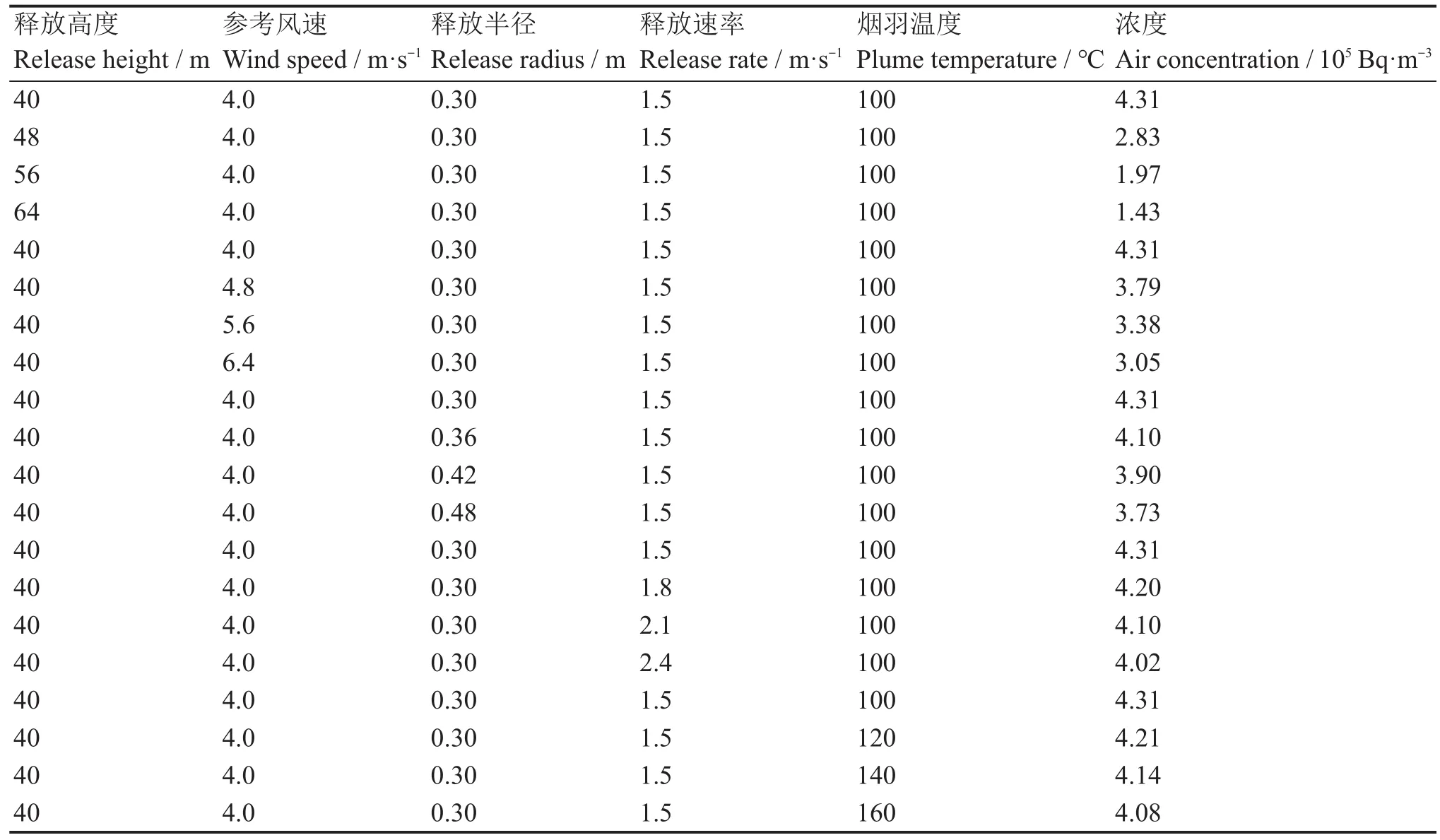
表1 一次一个变量法计算过程Table 1 Calculation process of one-variable-at-a-time approach

2 贝叶斯MCMC方法

2.1 贝叶斯基本理论

贝叶斯理论最早由英国学者贝叶斯在18世纪中叶提出，在20世纪50年代后，贝叶斯理论得到了应有的重视，并开始在统计决策问题中得到广泛应用［15］。贝叶斯理论的核心是贝叶斯公式，可以表示为：

式中：θ为模型输入参数构成的向量；p(θ)为这些参数的联合先验概率密度；p(z|θ)为模型输出值与实际观测值z在输入参数向量θ时的相似度，通常用似然函数表示。

2.2 MCMC方法

由于高斯烟羽模型经修正后很难找到准确的计算表达式，无法直接应用贝叶斯公式求解参数不确定性，因此采用了马尔科夫链蒙特卡罗方法（Markov Chain Monte Carlo，MCMC）来耦合贝叶斯方法和高斯烟羽模型［16］。常用的MCMC算法有Metropolis-Hastings算法、Gibbs抽样和自适应Metropolis算法等。下面介绍MCMC方法的自适应Metropolis算法［17］：

1）按照先验分布随机抽样产生初始样本向量θ0；

2）产生候选样本向量：由期望为上个样本向量θt-1及协方差矩阵为Ct经随机抽样产生候选样本向量x，其中：

式中：t0为初始化阶段的样本数；C0为初始协方差矩阵；COV(θ0，θ1，…，θt-1)表示所有已有的样本向量的协方差；Id为维数是样本向量维数d的单位矩阵；ε是一个很小的数，用于防止协方差降为0；sd是一个比例因子，用于保证合适的接受概率，此处sd=2.42/d［18］。

协方差矩阵可由式（4）计算：

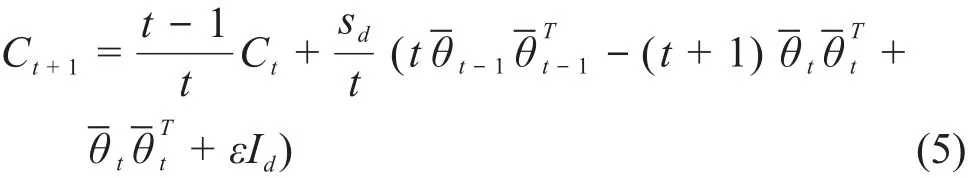
3）产生样本向量θt：以候选样本向量作为模型的输入参数，得到模型计算结果，然后以下面的接受概率确定是否接受候选样本向量：

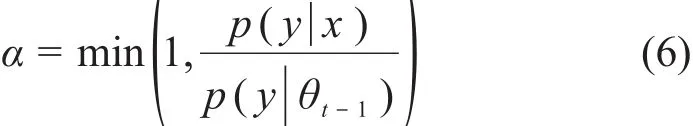
同时随机抽样取一个0～1之间的随机数μ，若μ≤α，则θt=x，反之θt=θt-1。

4）重复步骤2）和步骤3），直到获得足够数量的参数样本向量。

5）判断样本向量是否收敛到贝叶斯后验分布。

3 高斯烟羽模型不确定性分析

3.1 获得观测资料

由于核电厂放射性物质泄漏事故的观测资料难以获得，因此本文使用大气扩散程序生成模拟数据作为观测资料使用。将假设的理想气象条件输入到程序中，得到几个观测点处的大气放射性浓度作为观测资料。生成模拟观测数据时，释放高度设置为50 m，参考风速设置为5.0 m·s-1。观测点高度设置为1.5 m，共设置了5个观测点，分别位于下风向0.5 km、0.8 km、1.0 km、2.0 km、5.0 km处。

3.2 似然函数

在贝叶斯分析中，将模型输入参数中的释放高度和风速作为随机变量。似然函数的形式为：

式中：θ表示参数样本向量；i=1，2，…，n，n为观测点数；F是一个算子，表示将参数样本输入到模型中计算得到的指定观测点的空气放射性比浓度值；z*i表示第i个观测点的空气放射性比浓度观测值。

3.3 MCMC方法应用于高斯烟羽模型

3.3.1 确定先验分布

自适应Metropolis算法相比于其他MCMC算法的最大优势在于不再需要严格确定参数的先验分布类型，只需要确定输入参数可能取值的范围即可［19］，因此本文假设释放高度和10 m高度处的风速的先验分布为均匀分布，分布范围如表2所示。

3.3.2 MCMC抽样

先验分布确定后，初始协方差矩阵选为参数先验分布范围的1/20，较小的初始协方差矩阵能使得MCMC样本序列更快收敛。初始化阶段样本数为200，总的采样样本数为40 000。图1和图2给出了样本均值和标准差随迭代过程的变化曲线。

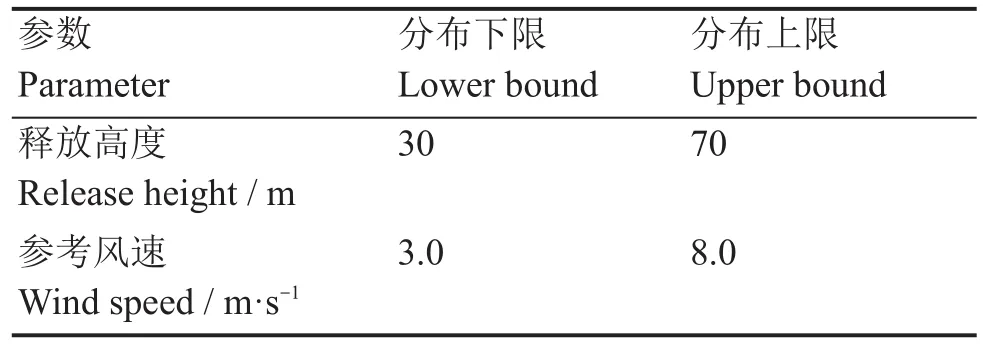
表2 输入参数的先验分布Table 2 Prior distribution of input parameters

图1 输入参数样本均值的变化曲线(a)释放高度，(b)参考风速Fig.1 Sample mean change curve of input parameters(a)Release height,(b)Wind speed

从上面的样本序列均值和标准差变化曲线可以看出，在20 000次采样之后，样本序列的均值和标准差曲线的波动幅度均较之前大大减小，即趋于稳定。除上述判断标准外，Gelman等［20］提出了基于多个采样序列的收敛判断方法：

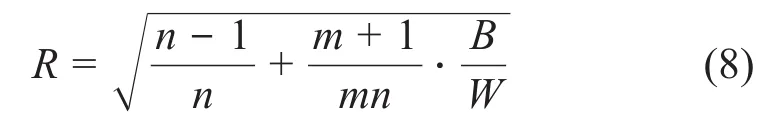
式中：R为比例降低系数，它的值越接近1，说明样本序列越趋于收敛；n为每个样本序列的采样数；m为样本序列数；B/n为样本序列的均值之间的标准差；W为样本标准差之间的均值。

图2 输入参数样本标准差的变化曲线(a)释放高度，(b)参考风速Fig.2 Sample standard deviation change curve of input parameters(a)Release height,(b)Wind speed

为减少采样偶然性的影响，并使用上述收敛判断方法，重复进行了3次MCMC采样，每次获取40 000个样本。计算得出采样过程中R的变化曲线，如图3所示。

可以看出，在采样初期，比例降低系数R变化剧烈，呈现波动下降趋势；在20 000次采样以后，两个输入参数的R值都相当接近1，这说明此时MCMC序列已经收敛。

3.4 样本序列分析

从上一步的分析可知，样本序列在20 000次采样之后收敛，因此取每个样本序列的后20 000个样本，这样就得到了60 000个收敛到贝叶斯后验分布的样本及其对应模拟结果。对其进行分析得到每个观测点处的大气放射性浓度值的最小值、最大值、众数以及标准差，如表3所示。

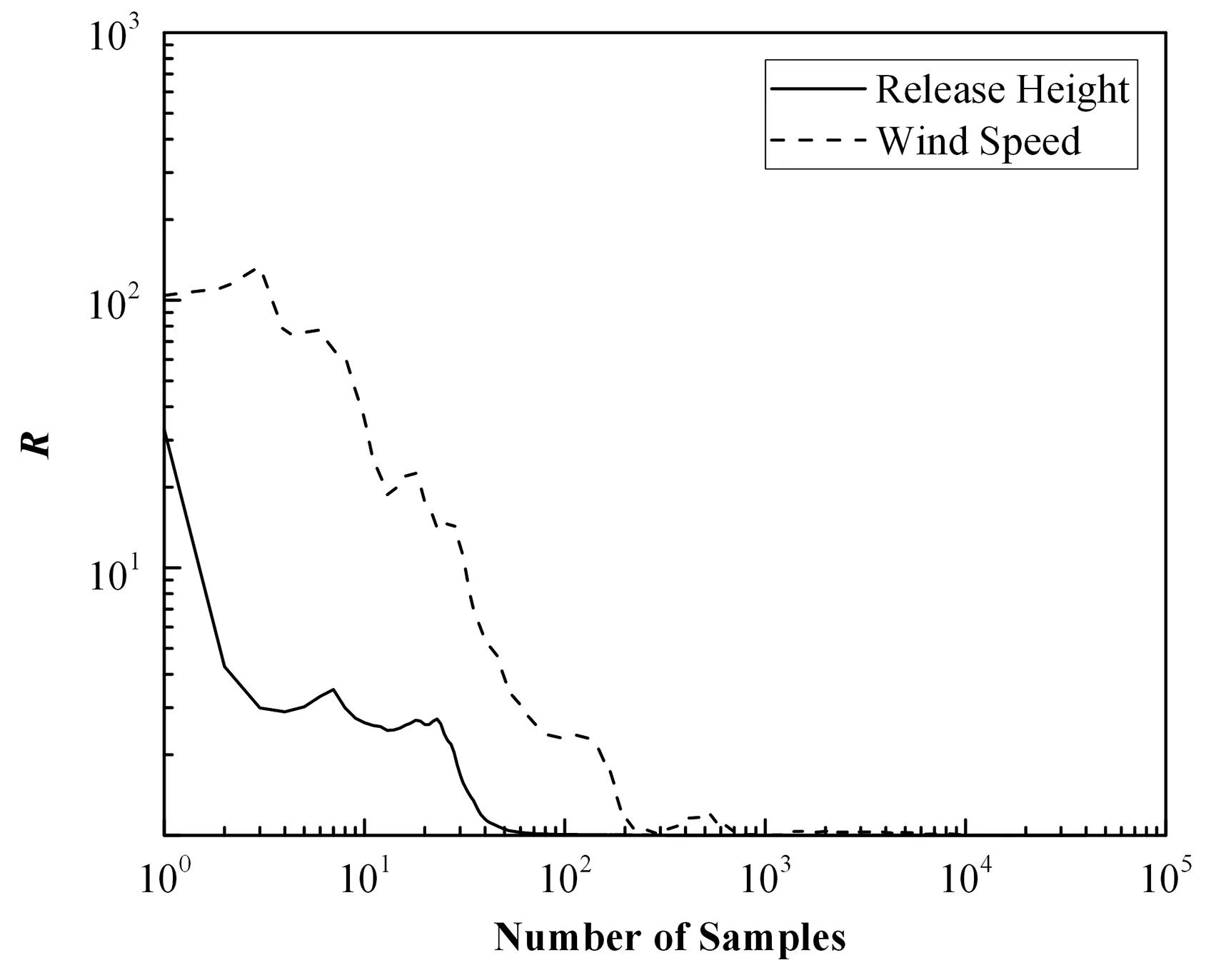
图3 采样过程中的比例降低系数Fig.3 The scale reduction score during sampling

表3中的众数并不是传统意义上出现次数最多的一个值，而是将样本的取值范围从小到大平分为50组后，取样本点最多的一组的中间值作为众数，这个值是模拟结果和观测值相差最小的数值，可以认为是观测资料的最优拟合。由于收敛到后验分布的样本序列符合正态分布，因此模型结果也符合正态分布，统计模型结果的数值分布可以获得置信区间。据此绘制出观测资料的最优拟合曲线以及模拟结果的95%置信区间如图4所示。

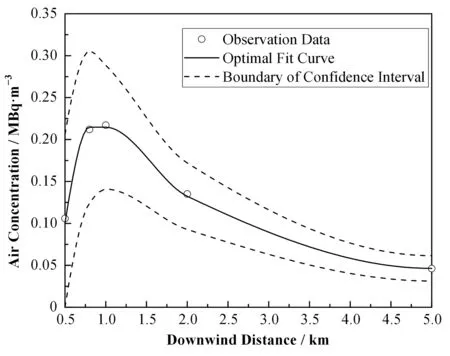
图4 观测资料的最优拟合及模拟结果的95%置信区间Fig.4 Optimal fitting and simulation results of observation data in 95%confidence interval

表3 模型结果序列分析Table 3 Analysis of model results series

4 结语

相比于传统的不确定性分析方法，贝叶斯方法充分利用了已有的观测资料和参数先验分布信息，其结果更加可靠，得到的置信区间的可信度也更高。马尔科夫链蒙特卡罗方法可以方便地耦合大气扩散模型和贝叶斯方法，避免了贝叶斯公式中归一化常数的求解，因此可以很好地应用在难以寻求解析式的模型中。

根据MCMC方法样本序列对应的模型模拟结果的众数和标准差数据分析，可以得到观测值的最优拟合和置信区间，从而为事故后应急响应提供更加可靠的数据参考，有效降低决策失误的风险。