基于无线信号K-M模型的三维室内定位算法研究

马丽萍 王 忠 徐慧君 何承恩

(四川大学电气信息学院 四川 成都 610065)

0 引 言

常见的室内无线WLAN定位技术主要分为基于信号位置指纹识别法[1]和基于信号传播模型法。位置指纹识别法在离线阶段时，由于室内障碍物会使信号发生反射、散射，出现多径效应[2]，导致接收到的信号强度(Received Signal Strength，RSS)常发生比较大的波动，建立的指纹数据存在较大的误差；在线数据匹配阶段时，一旦某个或某几个信号接入点(Access Point,AP)信号被切断，定位误差将大大增大，且存在后期需定期更新指纹数据库、局限于二维平面定位等缺点。传播模型法为通过预先获得信号传播的数学模型，将待测点接收的无线电信号强度大小转换成物理距离的方法。无线信号传播模型分为确定性模型和经验模型。确定性模型存在复杂度高、无线递归、实际应用低等问题；经验模型用影响信号传输的参数构建信号的距离衰减模型，经济实用。常见的室内经验传播模型有衰减因子模型、对数路径损耗模型、马特内-马恩纳模型(Keenan-Motley，K-M)、多墙模型等[3]。

近年来学者对无线信号经验传播模型进行修正，文献[4]指出常见的经验模型中路径损耗因子为固定不变的常量，未考虑到环境的动态变化，因此增加了一定地时效性，对路径损耗因子进行修正，在一定程度上提高了信号测距的准确度。文献[5]采用BP神经网络训练对数路径损耗模型，将RSS值输入BP神经网络输出得到AP到RP的距离。但由于BP神经网络在误差反向传播中，梯度下降法容易陷入局部极值点，因此建立稳定的模型，精确预测AP与RP之间的距离是本文的重要环节。

基于RSS的三维加权质心定位算法研究如下：普通三维质心算法采用未知节点通信范围内的所有信号接入节点的几何质心来估算未知节点位置，此方法只适用于节点分布均匀的情况下，若锚节点分布不均匀，则其定位精度极低。文献[6]对普通质心算法加以改进，提出基于距离的三维加权定位算法，选择未知节点周边的K个信号接入点，计算未知点与接入点之间的距离，以距离的倒数作为改进后质心算法的加权系数。该算法相较于传统质心算法对定位精度有很大的提高，但若无线接入点处于同一高度，不能实现真正意义上的三维定位。文献[7]提出12点质心定位法，即选择4个空间球体，每两个球心连线与球面出现12个交点，求解12个交点组成的多边形的质心，但12个点选择限制在空间球面上，对质心的计算会产生较大的偏差。文献[8]提出了基于距离和指数函数的三维加权质心定位算法，对加权因子进行修正，避免了传统三维质心法中次要接入节点的信息被淹没，数据表现更为平滑，但此算法对接入节点的覆盖率要求较高。文献[9]提出坐标四面体实心算法，其思想为基于距离权重和测量误差双修正质心法，但限制条件较多，实际情况不适用。文献[10]采用极大似然估计法，但在测距定位中信号容易受到障碍物阻碍、多径传播等因素的干扰，导致定位精度较低。文献[11]提出了空间球交会的三维加权质心法，任意2个球体构成空间球体对，根据空间球体对的位置关系得到加权因子，针对不同的情况具体分析，但此算法计算繁琐，误差较大。目前各种加权质心法误差较大，且室内环境复杂，如何改进加权质心法来提高室内定位精度，为本文研究的另一重要环节。

因此，为了提高定位精度实现三维定位，本文提出了一种基于无线信号K-M模型的三维室内定位算法。首先利用径向基函数(Radial Basis Function，RBF)的非线性特性模拟室内传播的复杂性，建立无线信号K-M传播模型，采用改进粒子群算法(Particle Swarm Optimization，PSO)优化RBF神经网络参数，避免算法陷入局部最优；再采用极大似然估计法(Maximum Likelihood Estimation，MLE)求解采样方程组的最小二乘解；最后使用改进RSS-d加权因子修正最小二乘解误差，提高定位精度，得到RP的三维坐标，从而实现未知节点的三维定位。

1 建立无线信号K-M传播模型

1.1 K-M模型

在室内环境下，由于建筑物结构复杂性、门窗、家具、电器及人员走动等都会导致无线信号衰减，Keenan和Motley充分研究了无线信号发射点到接收点之间，由不同材质类型的墙壁和地板对信号衰减的叠加以及周围环境对信号造成的衰减，提出了非视距传播情况下的K-M传播模型。

(1)

式中：PL(d)表示距离信号发射点为d的位置点接收功率；d0为参考距离，其值通常取为1米；ζ是信号衰减因子(一般为2～5)，取决于周围环境的复杂度;Ki、Fi分别表示楼层数目及对应材质地板的衰减因子；Ij、Wj分别表示墙壁数目和对应材质墙壁的衰减因子。

1.2 RBF神经网络训练K-M测距模型

RBF神经网络是一种单隐含层结构的前馈型神经网络，结构简单，收敛速度快，具有很强的逼近任意非线性连续函数的能力[12]，已广泛应用于各个领域的建模中。本文采用多输入单输出的网络结构，实验样本以多向量X为输入、单向量y为输出。训练K-M测距模型如图1所示。

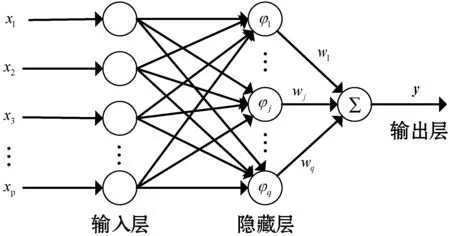
图1 RBF神经网络的结构

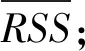
(2)

(3)

采用减聚类法[13]确定隐含层神经元的个数q。改进PSO优化RBF神经网络的3类参数：基函数中心Cj、基函数方差σj、连接权值wj。

1.3 改进PSO优化RBF网络参数

PSO中每个粒子有位置、速度和适应度三项特征，在每一次迭代中通过个体极值和群体极值更新自身的速度和位置，即：

(4)

(5)

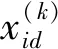
(6)

本文在此基础上再对惯性权重因子w(k)进行改进，用非线性动态递减方法更新权重因子w(k)。

(7)

式中:Tmax为最大迭代次数，初始惯性权重ws=0.9，终止惯性权重we=0.4。

在算法初期曲线缓慢下滑，以保证权重较大，有利于跳出局部最优，后期曲线快速下滑，以较小的权重加快算法的收敛，如图2所示。

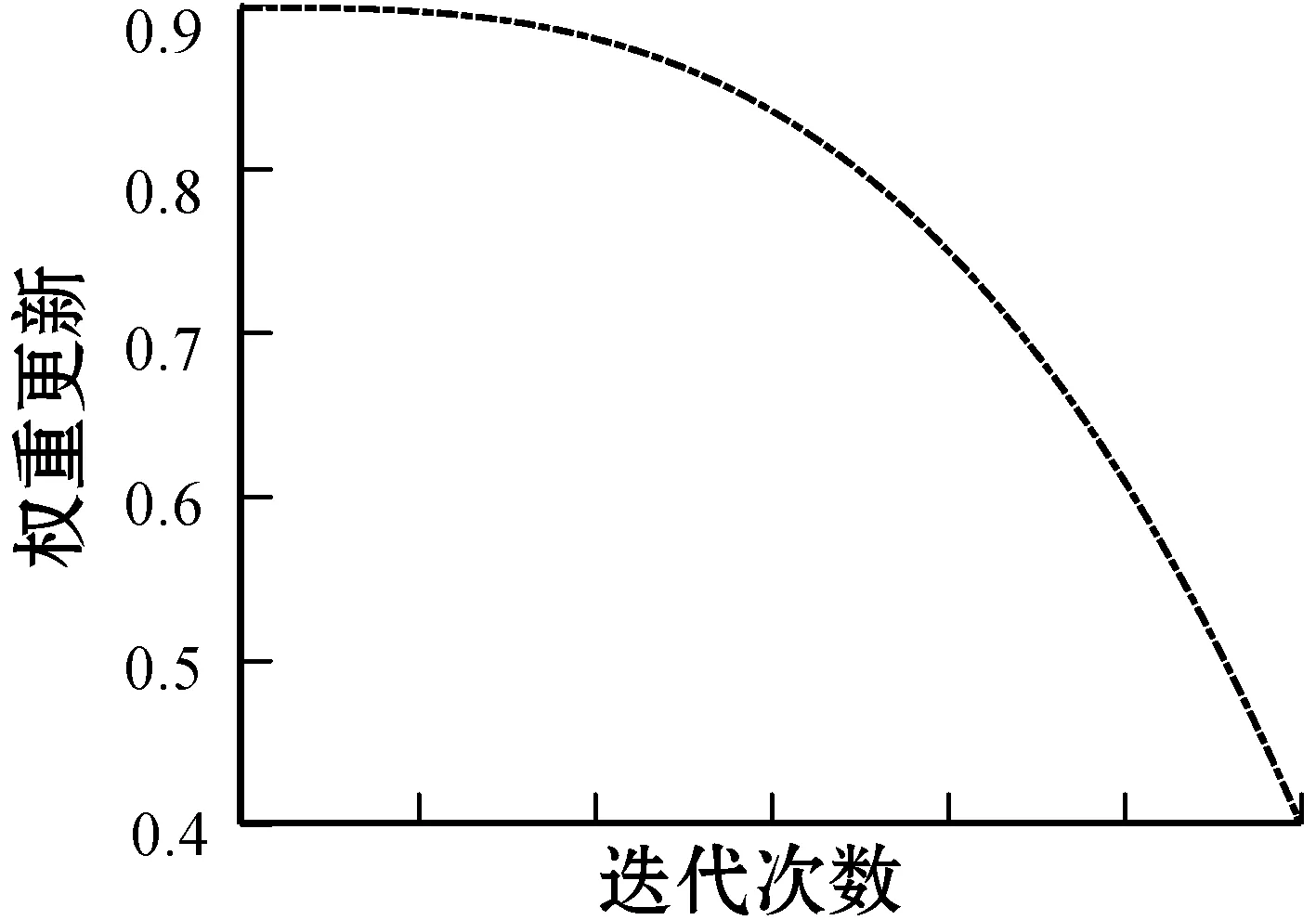
图2 惯性权重迭代

将RBF神经网络的基函数中心Cj、基函数方差σj、权值wj作为优化参数，以样本实际输出距离与网络输出距离之间的均方根误差作为适应度函数，构造粒子群优化模型。

(8)

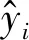
改进PSO确定RBF网络参数步骤如下：

步骤1使用减聚类算法进行聚类分析，得到隐含层神经元个数q，确定网络结构；

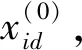
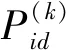
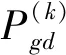
步骤6根据式(4)更新速度、式(5)更新位置、式(6)更新加速因子、式(7)更新权重因子；

步骤7重复步骤4-步骤6，直到满足两次误差阈值小于10-5或达到最大迭代次数跳出循环；

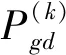
2 相关方法

2.1 MLE采样方程组法

假设有n个信号接入点AP为(xi,yi,zi)(1≤i≤n)未知节点RP位置坐标为(x,y,z)，以AP为球心，AP与RP之间的距离di为半径,其中距离di由PSO-RBF测距模型获得。构造空间球体列出方程组：

(9)

将其中每个方程式减去最后一个方程式可得：

(10)

(11)

令X=(x,y,z)T，式(11)可表示为AX=B，理想情况下方程组有唯一解，即为图3中的K0。但在实际情况中，由于样本数据测量误差，导致改进PSO-RBF传播模型输出AP与RP之间的距离d存在误差，且一般情况下方程组中n≥3存在最小二乘过确定问题，导致方程组无解。求解该问题，传统采用极大似然估计法求得RP的估计位置，即求解方程组的最小二乘解X=(ATA)-1ATB，在求解的过程中，因消除了一次项，导致RP估算位置与真实位置误差较大，如图3中位置K1所示。

图3 MLE采样方程组法

2.2 RSS-d加权质心法

(12)

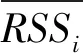
由式(13)求解未知节点RP坐标为(x,y,z)，位置如图3中K2所示。

(13)

3 多元算法过程

1) 采集样本数据，训练PSO-RBF测距模型。

2) 以AP坐标与测距模型输出距离d构建方程组，采用个MLE采样方程组法，求取m个点坐标估计值。

3) 采用RSS-d加权质心算法，对m个坐标估计值进行加权计算，得到未知节点的坐标。

4 采取样本数据

4.1 选取实验环境

实验场景为四川大学望江校区基础教学楼B座二楼，如图4所示。

图4 实验场景图

该场景长、宽、高为45 m×40 m×4 m，总共有25个有效AP点。采用Fisher准则[16]选取稳定有效的20个AP点进行实验。在实验环境中随机选取18个参考点RP。记录AP点发射功率pi(1≤i≤n)及AP位置坐标(xi,yi,zi)(1≤i≤n)。

4.2 实验环境中的经验损耗值

通过实验，无线信号在室内不同障碍物场景中，距离AP距离1 m处的接收功率PL(d0)、信号衰减因子ζ见表1；无线信号穿过不同材质的墙壁损耗因子F值见表2；无线信号穿过不同材质的地板损耗因子W值见表3。

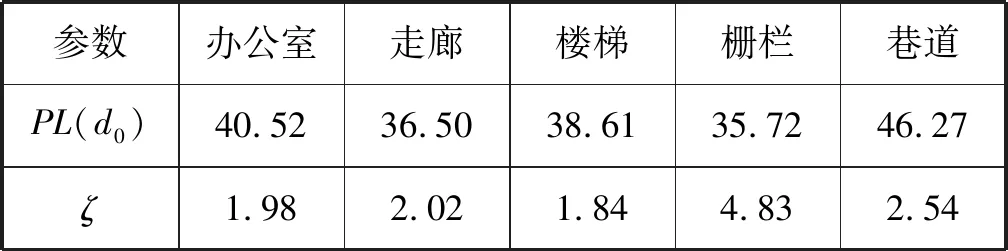
表1 不同环境下的距离AP距离1 m处的 接收功率及信号衰减因子 dB

表2 不同材质的墙壁的损耗因子 dB

表3 不同材质的地板的损耗因子 dB

4.3 RSS预处理

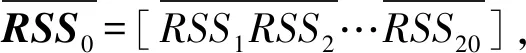
图5 RSS的数据预处理

4.4 一个训练样本

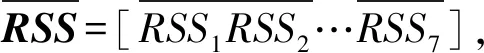
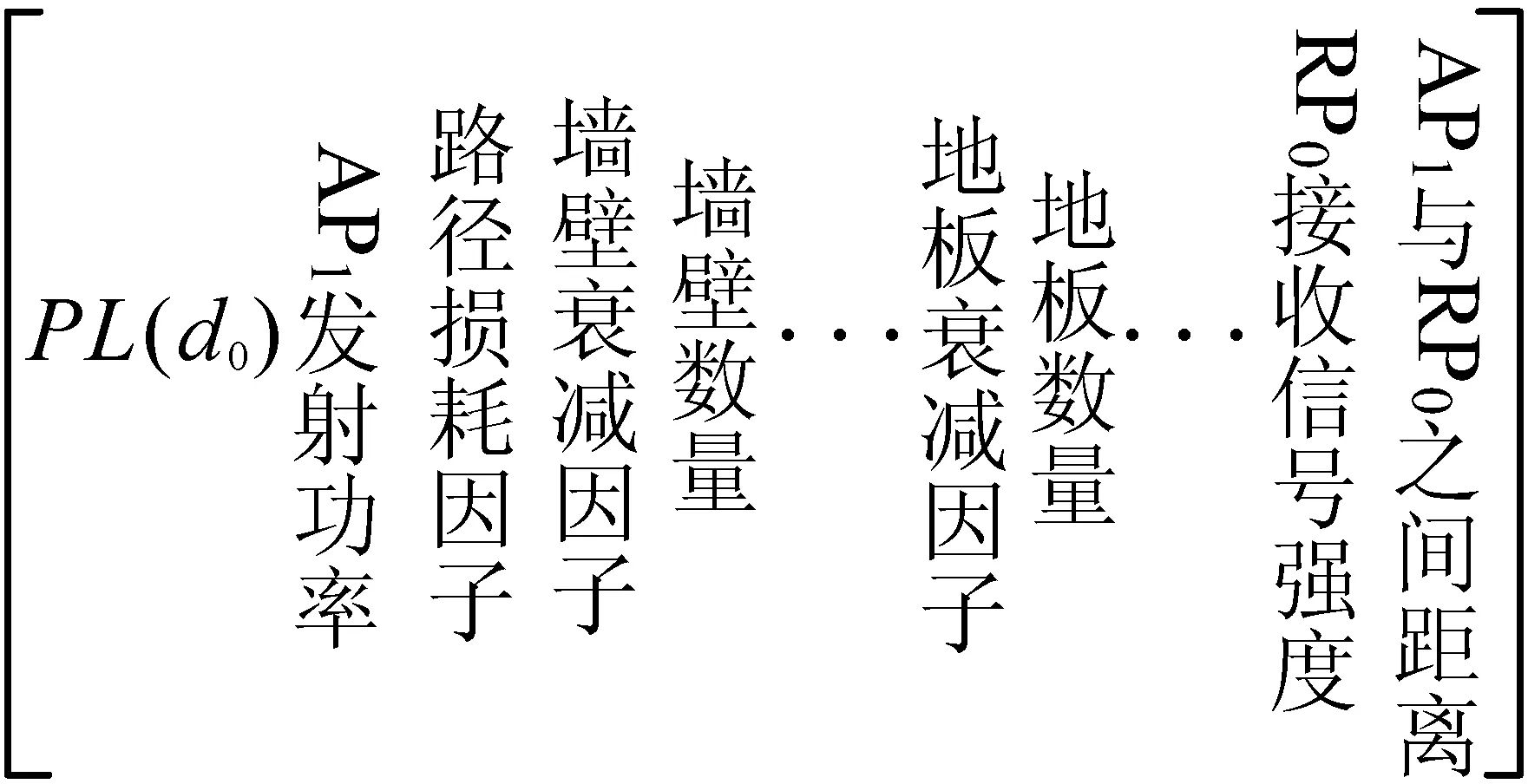
图6 RP0与AP1一维数据向量

5 实验仿真

5.1 改进PSO-RBF训练K-M测距模型

在400个样本集中，随机挑选300个样本作为训练集，50个作为交叉验证集，50个作为测试集。初始化粒子种群为N=20，最大迭代次数Tmax=300，训练结果如图7所示。可以看出，经过250次粒子的自适应度值趋于稳定σ=0.04，将此时的自适应权重作为RBF神经网络的Cj、σj、wj参与训练。

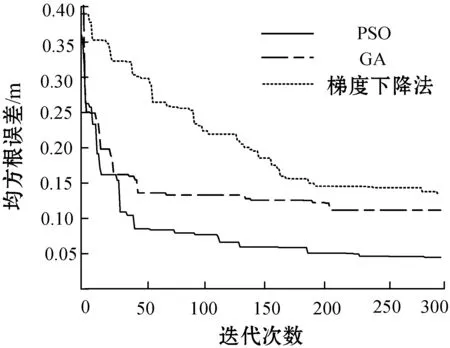
图7 最小误差进化过程

为了验证本文方法的有效性，使用改进PSO优化RBF构建无线信号K-M测距传播模型，分别采用RBF神经网络、GA遗传算法优化RBF、PSO粒子群算法优化RBF这3种方法进行实验，实验对比结果如图8所示，误差对比见表4。

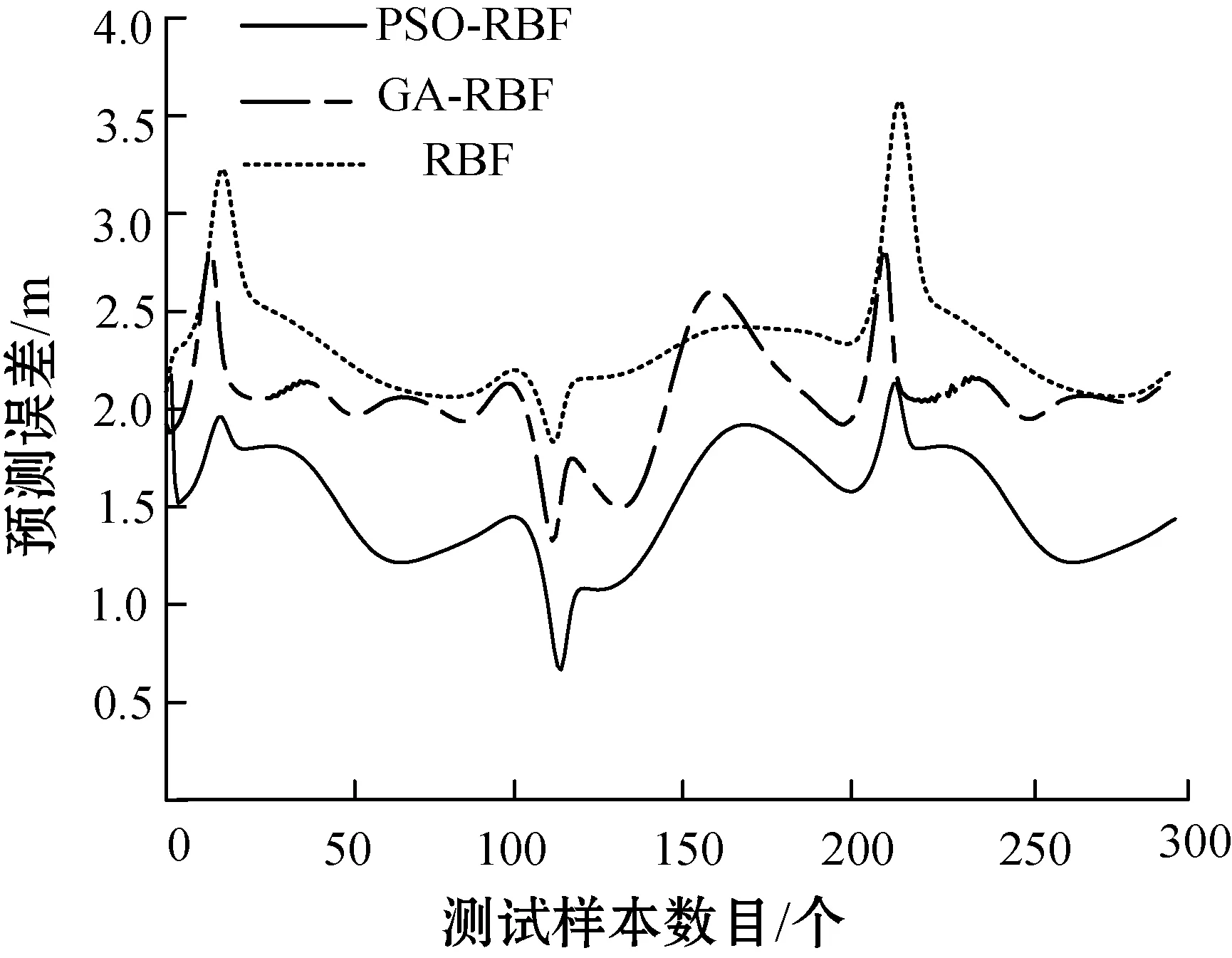
图8 三种算法误差对比

表4 详细误差数据 m

可以看出，RBF和GA-RBF的网络预测距离输出与实际的距离误差较大，相比之下，PSO-RBF的距离预测输出与实际距离更为接近，误差最小，预测效果更稳定。

5.2 MLE采样方程组法与RSS-d加权质心法

图9 4种算法定位结果比较

表5 4种算法求解RP点坐标的误差对比 m

实验结果表明，在实验环境中随机选取了18个RP点，与其他三种算法的结果相比，算法4的结果中有16个数据点更靠近真实RP位置，三轴平均误差为x轴1.55 m、y轴1.48 m、z轴0.98 m，因此算法4表现最优。

6 结 语

本文提出了建立无线信号的经验传播模型，采用RBF网络的非线性特性模拟室内环境的复杂性，改进PSO优化网络参数；提出了MLE采样方程组及RSS-d加权质心的思想求解未知点的坐标。建立无线信号传播模型，需要足够多样本来不断修正模型参数，因此需要采集大量的数据，增加了一定的工作量，计算复杂度较高。由于建筑物环境十分复杂，本文信号的信号衰减经验模型主要考虑了实验整体环境、墙壁和地板和对信号衰减的影响，实际中还有一些其他不确定性因素如人流量、信号干扰等。因此完善不确定因素、建立稳定可靠的传播模型将是下一步的工作重点。