智能RGV动态调度多目标规划模型

卫 巍 杨志辉 谢浩然 胡倚薇

1(东华理工大学化学生物与材料科学学院 江西 南昌 330013)2(东华理工大学理学院 江西 南昌 330013)3(东华理工大学地球物理与测控技术学院 江西 南昌 330013)

0 引 言

自1954年以来，学者们对生产调度问题进行了大量的研究。但是由于以往的生产调度模型都使用了大量的前提与假设，造成其模型在生产实践中很难被应用[1]。因此，对于更符合实际情况下的柔性作业车间调度问题(FJSP)具有非常重要的研究价值[2]。

21世纪，针对FJSP问题常使用启发式的方法对问题进行研究求解。Ho等[3]对FJSP使用组合分派方法；Chen等[4]用图论模拟分段为两部分染色体求解FJSP；王雷等[5]考虑快速解码算法避免非法解产生，通过精英策略提高求解效率和求解的总适应度；张晓星等[6]通过研究最大完工时间及总加工能耗，使用混合蛙跳算法求解FJSP，得到不同权重下的调度方案；Kato等[2]将问题分为粒子群优化(Particle Swarm Optimization,PSO)，及随机重启爬山(Random-Restart Hill Climbing,RRHC)；Zandieh等[7]模拟了FJSP基于状态的维护(Condition Based Maintenance,CBM)，并考虑Sigmoid函数和高斯分布的组合改进CBM，提出了一种改进的帝国竞争算法(Imperialist Competitive Algorithm,ICA)；Gao等[8]提出了一种改进的人工蜂群(Improved Artificial Bee Colony,ABCIABC)算法，其中基于处理时间的不确定性，将其建模为模糊处理时间；赵诗奎[9]对已有邻域进行精简与有效移动的拓展，提出了融合改进邻域的混合算法；张新等[10]对入侵杂草算法做出了新的改进；徐文豪等[12]对花授粉算法对问题的解进行离散化，在过程中为平衡前期全局搜索能力与防止后期陷入局部优解引入自适应正则化因子。

在实际生产中，存在FJSP问题未考虑实际因素。在近年来，国内外学者对实际问题的不同方面进行了分析。Lin等[13]对工件运输过程消耗的时间进行考虑，使用集成的GA-GSO-GTHS(Genetic Algorithm-Glowworm Swarm Optimization-green tra-nsport heuristic strategy)算法解决问题；Zhang等[14]与张国辉等[15]分别对FJSP问题在生产过程中绿色制造问题进行了考虑，前者开发了基于动态博弈的双层调度算法，后者构建了碳排放的定量模型，通过多目标求最值获得最优解；Yazdani等[16]对流水线最早与延迟两类情况分别的总时长作为目标函数，针对问题的复杂性，构建了基于有效邻域混合的帝国竞争算法(ICA)；Rahmati等[17]考虑了纠正性维护(Corrective Maintenance,CM)和预防性维护(Preventive Maintenance,PM)方面的两种维护方案，同时对多步骤间的加工过程进行了考虑。

针对现有方法对于机器出现故障[18]时的调度考虑以及系统的稳定性[19]方面考虑不足的局限，本文提出改进的遗传算法编码方式及求解方法。通过结合多因素、多目标的问题特征构建编码方式，利用改进的遗传算法对加工次序进行求解，得到一组与最优解总时间差距不大的较优解。该方法不仅可以方便快速地求解此类问题，还可以提升此类问题的可解释性和准确程度，并且得到优化的编码形式更利于人们理解。

1 改进遗传算法解决RGV调度问题

1.1 相关工作

遗传算法最早由美国密执安大学Holland教授[20]根据物竞天择理论于20世纪60年代提出,至20世纪80年代形成基本的框架。2005年，江雷等[21]将遗传算法并行化求解旅行商问题(Traveling Salesman Problem，TSP)，此算法进一步提高了种群的多样性和结果的准确性。

RGV是一类可以根据指令自动控制移动方向和距离、作用是搬运物料的智能车，并且此智能车运行在固定轨道上，自带一个机械手臂、两个机械手爪与物料清洗位，可以对上下料及清洗物料等作业任务进行操作完成，进一步提升了加工的效率，并体现了其相对的智能性。

车间调度问题(JSP)作为一个最为常见的NP hard问题，它的调度目标就是事先得到机器加工工序的时间，最终使得耗费的资源最少。柔性作业车间调度问题(FJSP)是以上问题的扩展问题。1990年，Bruker等[22]首次提出了FJSP的概念，即带有机器柔性的JSP问题。与上述问题不同的是，柔性作业车间调度问题则是工件不确定其加工机器，也不确定加工工序，其灵活性较高，因此，此类问题是个有待解决的热门问题。

(1) 此问题属于NP难问题，大多数解法或多或少都会陷入局部收敛的障碍；

(2) 机器在运作中还会有一定可能发生故障，从而影响整体结果。

针对上述不足,本文根据FJSP问题对遗传算法进行改进，减少局部收敛出现的概率，使改进后的方法所得到的解更接近最优解。

(1) 在解决陷入局部收敛方面，将遗传算法编码分为机器选择部分、工序排序部分、故障概率部分和工序分配部分；

(2) 在解决故障影响方面，本文引入了机器故障概率和机器维修时间概念。

本文中，智能RGV动态调度问题的解决方法是通过使用解决柔性车间调度问题的方法来解决的。其问题本身就是一类在柔性前提下的作业车间调度问题，因而两者一个为实际问题，一个为构建的模型，并通过对此模型的求解得到智能RGV问题的调度方案。

1.2 问题描述

智能化RGV动态调度问题中，智能RGV要在n台机器之间来回移动ω个独立物料。其中工件集合为I={I1,I2,…,Im}，机器集合为J={J1,J2,…,Jm}，不确定每个工件的加工机器，也不确定加工不同工件的工序的先后顺序，因此具有较大的灵活性。其中：工件具有H道工序；Oih表示第i个工件的第h道工序，每个Oih可以在相容的机器上任意加工，且不可重复加工同一个工件的同一道工序；pijh表示工件i的第h道工序在机器j上加工时间。在日常的加工过程中，除了机器加工时间之外，RGV移动、物料上下料、清洗加工完成的工件都是不可忽略的。因此本文引入以下参数：eijh表示工件i的第h道工序在机器j上加工结束时间；qijh表示工件i的第h道工序在机器j上下料所需时间；a表示RGV完成一个物料清洗作业所需时间；rijh表示工件i的第h道工序移动到机器上的时间。然而某些突发性事件，比如机器加工中途的损坏，也可能会极大地影响加工的结果，形成拥堵现象，显著降低效率和稳定性，得到的调度结果由于这样的现象因而无法适用于实际的加工中，或者说由于效率和稳定性的不足，只能适用于特定的加工环境中，不具有通用性。为此本文也引入了第i次维修所花的时间di、工件在机器加工时损坏的平均概率Eerr和用Nij表示工件i在机器j上是否发生故障，且假设工件一旦在加工时发生损坏后就不能再次加工或者当作成品使用，即当作废料处理，这将显著提高本问题在实际应用中的实用性。因此，如何得到并解决具有最优的系统稳定性和加工效率的动态调度多目标规划模型是一个具有实际意义的问题。

1.3 动态调度模型的建立

1.3.1模型的约束条件

根据实际生产中工序的加工顺序不同，并且一个工序不能同时在两台机器上进行。与之相对的，任意机器一次也只能加工一个工件，因此需建立如下约束条件：

(1)

(2)

eijhi≤Tii∈[1,n],j∈[1,ω]

(3)

(4)

(5)

(6)

(7)

bih≥0,eih≥0i∈[1,n],h∈[1,hi]

(8)

式(1)和式(2)表示第i个工件在工序上存在先后顺序，即工件的加工次序不可随意打乱，bijh表示工件i的第h道工序在机器j上加工开始时间，pijh表示工件i的第h道工序在机器j上的加工花费时间；式(3)表示任何一个工件的完工时间一定是小于最大完工时间，Ti表示最大完成时间，即加工所有工件的总时间；式(4)表示对一台机器不能同时加工两个工件，M表示一个足够大的正数；式(5)表示第i个物料加工第h道工序所花费的总时间，Pij表示工件i从开始向机器j移动到在机器上结束加工所需的总时间，包含工件的上下料时间、RGV的移动时间、机器加工时间以及完成一次清洗作业所需时间；式(6)表示任意时刻的一道工序只能在一台机器加工；式(7)表示任意时刻同时加工机器的总数一定小于机器总数，Lijh表示工件i的第h道工序是否在机器j上加工，其值为1表示肯定，反之0表示否定；式(8)表示任意变量参数必须为正数。

1.3.2存在故障的模型优化

根据实际情况，需考虑机器可能在工件加工过程中发生故障的作业情况，因此需要引入故障发生的概率及其发生的时间，增加约束条件，以保证模型的合理。

多道工序发生故障的动态调度模型相对上文，将所有bijh、eijh替换为sijh、cijh，其中：sijh表示考虑机器损坏时工件i的第h道工序在机器j上加工开始的时间；cijh表示考虑损坏时工件i的第h道工序在机器j上加工结束时间，在此之后增加如下约束条件：

(9)

di∈[Errmin,Errmax]

(10)

式中：Nij表示第i个工件的第j个工序是否发生故障，其中1表示发生，0表示不发生。

之后将式(2)、式(4)分别转化成：

(11)

(12)

式(9)表示工件i在机器j上加工发生故障的概率，本文中的概率设置为0.1；式(10)表示故障发生一次的时间的范围，di表示第i次发生故障维修时间，Errmin、Errmax表示故障维修的时间上下限；式(11)表示在存在损坏的前提下第i个工件的加工顺序存在先后关系，本文假定当机器发生损坏时，其加工工件当作废料丢弃处理，即丢弃的工件后一道工序的开始时间无限延期；式(12)表示在存在损坏的前提下同一时刻同一台机器能加工的工序是唯一的，tijh表示工件i的第h道工序在机器j上发生故障时此工序已加工时间。

1.3.3目标函数与综合评价函数

最终的目标是在加工工件的个数固定前提下时间达到最小，其目标函数是：

f1=min{Ti}

(13)

同时机器在加工过程中可能出现故障，为了量化目标在规定时间内加工的工件的相对优略，检验在消除损坏影响下的机器执行效率，故引入综合评价函数：

(14)

式中：α和β为各自权重；Ti1是无维修时的完成时间；Ti2是有维修时的完成时间，使得在保证加工系统的稳定性的同时也能保证加工的完成时间较小。

2 多分段遗传编码改进遗传算法

2.1 多分段遗传编码的构建

本文针对实际生产中的复杂情况设计了一种整数编码，由机器选择部分、工序排序部分、故障概率部分和工序选择部分四部分组成。

机器选择(Machine Selection,MS)部分：此部分染色体长度为T0。要求每个编码必须是整数,每一个编码中的整数代表当前工序选择的加工机器在可加工机器里的编号。这就保证了后续的操作都能得到可行解。

工序排序(Operations Sequencing,OS)部分：染色体长度为T0。采用整数编码，其中整数为工件号，工件号出现的先后顺序代表加工的先后顺序。这种方法使得编码更加稳定,也能保证后续的操作都能得到可行解。

故障概率(Failure Probability,FP)部分：染色体长度等于所有工件的工序之和T0。其顺序与工序排序部分的顺序相对应。其中：1表示机器出现故障；0表示机器正常运行，而在实际的生产过程中，对于加工损坏的工件是进行丢弃处理。

工序选择(Process Selection,PS)部分：染色体长度等于所有机器的个数T1。第j个空格表示第j个机器只可执行的工序。其中：空格中数字为1表示此机器加工第一工序；数字为2表示加工第二工序，以此类推。

染色体编码如图1所示，此处只例举工件1和工件2的所有工序。工件1的第一道工序有五台机器可选择进行加工，与之对应的4表示第四台机器是可加工的，即表示工件O11在机器上加工。而对于后续的工序排序部分，假设一开始进行加工的工序染色体为[22112]，其中第一个2代表第二个工件的第一道工序，即O21，故各工件的工序加工顺序为：O21-O22-O11-O12-O23。

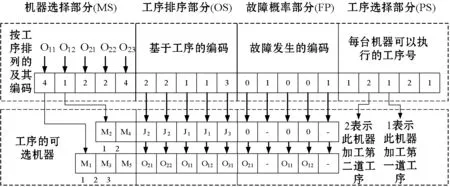
图1 多分段遗传编码

2.2 遗传算法的求解

2.2.1初始化

初始化是遗传算法中的第一步，T是最大进化代数，随机生成M个基因个体作为初始群体。本文根据需要考虑机器选择带来的机器负荷问题的原因，使用全局选择操作对染色体进行初始化，使得每个被选取的机器都能保证在工作，进而提高利用率。

全局选择的步骤如下：首先取一个长度与机器数目相同的整形数组，其中数组的序号依次为机器的序号，数组位置上的值初始化为0。随机选择当前要加工的工件，在可选机器中找到所花时间最小(工件移动到该机器的时间、机器上料时间以及机器加工工件的所需时间)的加工机器，将所选择的加工机器加工对应的数值更新到数组中，以此类推直到该工件加工完成。再重新选择一个工件开始，直到所有的加工任务完成。用全局选择方法可以保证机器加工时间最短的先被选中且机器加工的工作负荷平衡。

举例说明，假设第一次随机抽取到工件I1，第二次随机抽取到工件I2，则执行前两道工序的过程如图2所示。

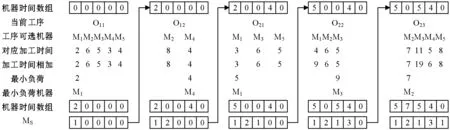
图2 全局选择流程图

2.2.2选 择

用上文全局选择方法对种群进行初始化后要执行选择操作，对机器选择、工序排序、故障概率和工序选择四个部分每次选取全局最优解中的90%，淘汰相对情况不太好的10%，以此得到最终较优的局部最优解。

2.2.3交 叉

对于选择进化出下一代的个体，随机找到两个不同的基因，根据交叉发生的概率，进行相互交换，产生新的下一代个体。交叉操作中一共分为机器选择部分、工序排序部分、故障概率部分以及工序选择四部分。

(1) 机器选择部分：为保证每个基因的先后顺序不变，此部分采用了均匀交叉的操作。主要步骤如下：

Step1在[1,T0]内随机产生一个整数r1，再随机得到r1个不同的整数；

Step2依据上述步骤得到整数r1，进而将父代染色体P1和P2内对应位置的基因根据目标位置机器数范围比例复制到子代染色体C1和C2中，保持它们的位置和顺序；

Step3将P1和P2余下的基因顺次复制到C1和C2中，保证它们的位置一致，顺序不变。

图3为机器选择部分的互换交叉过程。

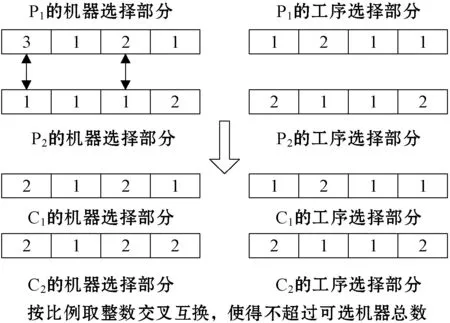
图3 机器选择部分的交叉

(2) 工序排序部分：将每个染色体中对多个工件进行操作，更好地继承父辈的优良基因。

Step1使得工件集{I1,I2,…，In}随机划分成两个不同的工件集；

Step2将父代染色体P1和P2中包含在上述划分的两个工件集中的工件复制到C1和C2，保证它们的位置一致，顺序不变；

Step3将P1和P2中不包括在上面划分的两个工件集中的工件复制到C2和C1，同时要保证它们的顺序不变。

图4为工序排序部分的互换交叉过程。

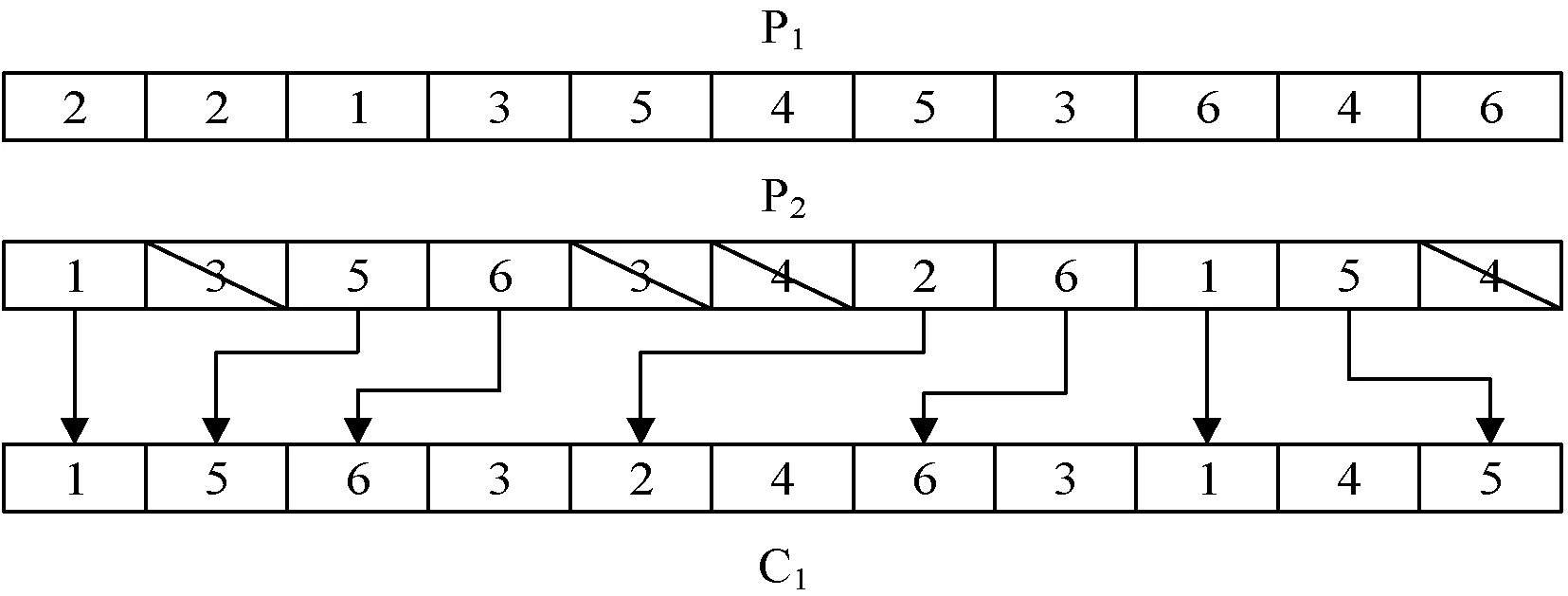
图4 工序排序部分的交叉

(3) 故障概率部分：

Step1在区间[1,T0]内随机产生一个整数r1，再次随机产生r1个互不相同的整数；

Step2将染色体P1和P2中对应的位置进行交叉。

图5为故障概率部分的互换交叉过程。

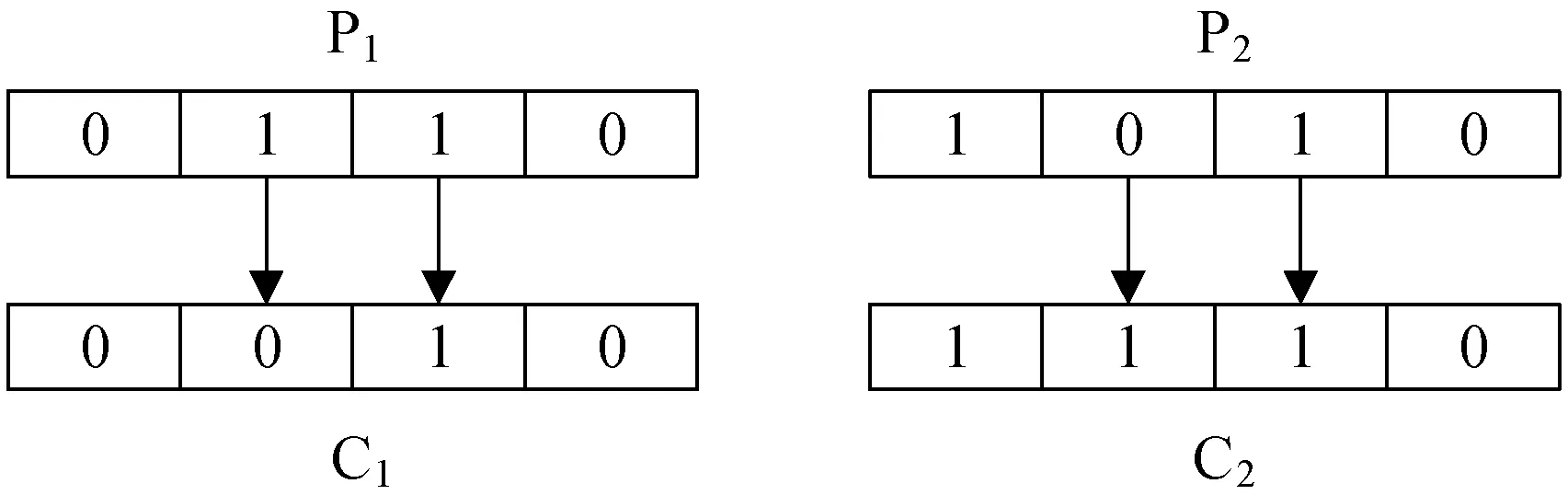
图5 故障概率部分的交叉

(4) 工序选择部分：

Step1在区间[1,T1]内随机产生一个整数r2，再随机产生r2个互不相同的整数；

Step2将染色体P1中r2个位置相互交换，P2以此类推。

图6为工序选择部分的互换交叉过程。

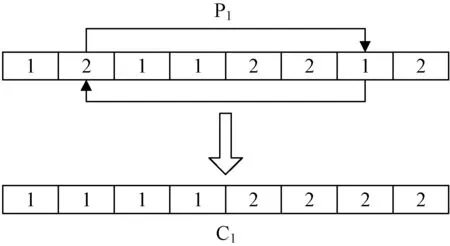
图6 工序选择部分的交叉

2.2.4变 异

变异通过对染色体的随机微小改变，使得产生一组新的个体，提高了种群多样性，并且一定程度上改变了局部搜索能力。

(1) 机器选择部分：

Step1在变异染色体中随机选取r1个位置；

Step2顺序选择所有的基因，对所有位置的机器设置为现在工序机器集合里可被选择且同时加工时间最短的机器。

(2) 工序排序部分：

Step1在变异染色体中随机选择r1个不同基因，然后根据选取基因生成此排序的所有邻域；

Step2将所有的邻域相应适应值进行评价，选出其中最优的个体作为下一子代。

(3) 故障概率部分：

Step1按照随机数r1再随机产生r1个互不相等的整数；

Step2将染色体P1和P2中对应的位置进行互换变异。

(4) 工序选择部分：

Step1按照随机数r1再随机产生r2个互不相等的整数；

Step2将染色体P1中r2个位置自身变异，变异成一个在工序数以内的随机正整数。

2.2.5创新特点

为了解决如何在机器的加工工序未知、引入机器故障的情况下选择出较优的加工分配方案的问题，本文在遗传编码中引入了工序排序部分和机器故障部分，提高了算法的并行性和准确性，进一步增加了此类问题结果的有效性。

3 算例实验

为了验证所建模型，本文使用一种在实际生产中被使用的智能化RGV动态调度测试算例进行验证。

根据不同的加工参数，此算法都能得到同时考虑系统稳定性和效率的解决方案，而不单单只考虑效率，并且不只使用同一种解决方案，体现了算法的动态性。

假设情况中可进行加工的机器共有8台，由1辆轨道式自动引导车(RGV)、8台计算机数控机床(Computer Number Controller，CNC)、1条直线轨道、1条下料传送带、1条上料传送带等附属设备组成，模拟图如图7所示。

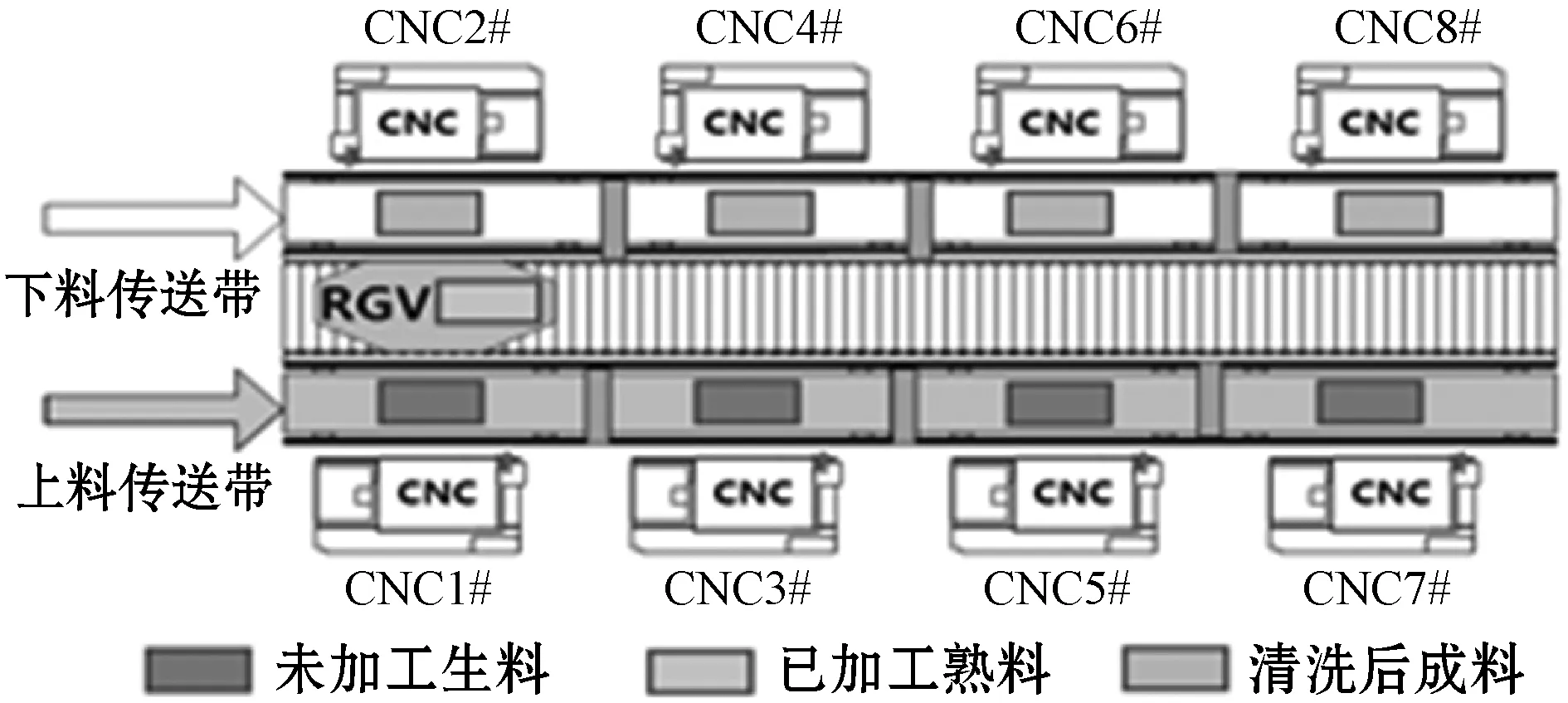
图7 智能加工系统示意图

由于尚没有可靠的标准算例可以用于此类柔性流水车间调度问题并被验证可靠，因此将其工作时的相关参数进行如表1所示的定义。

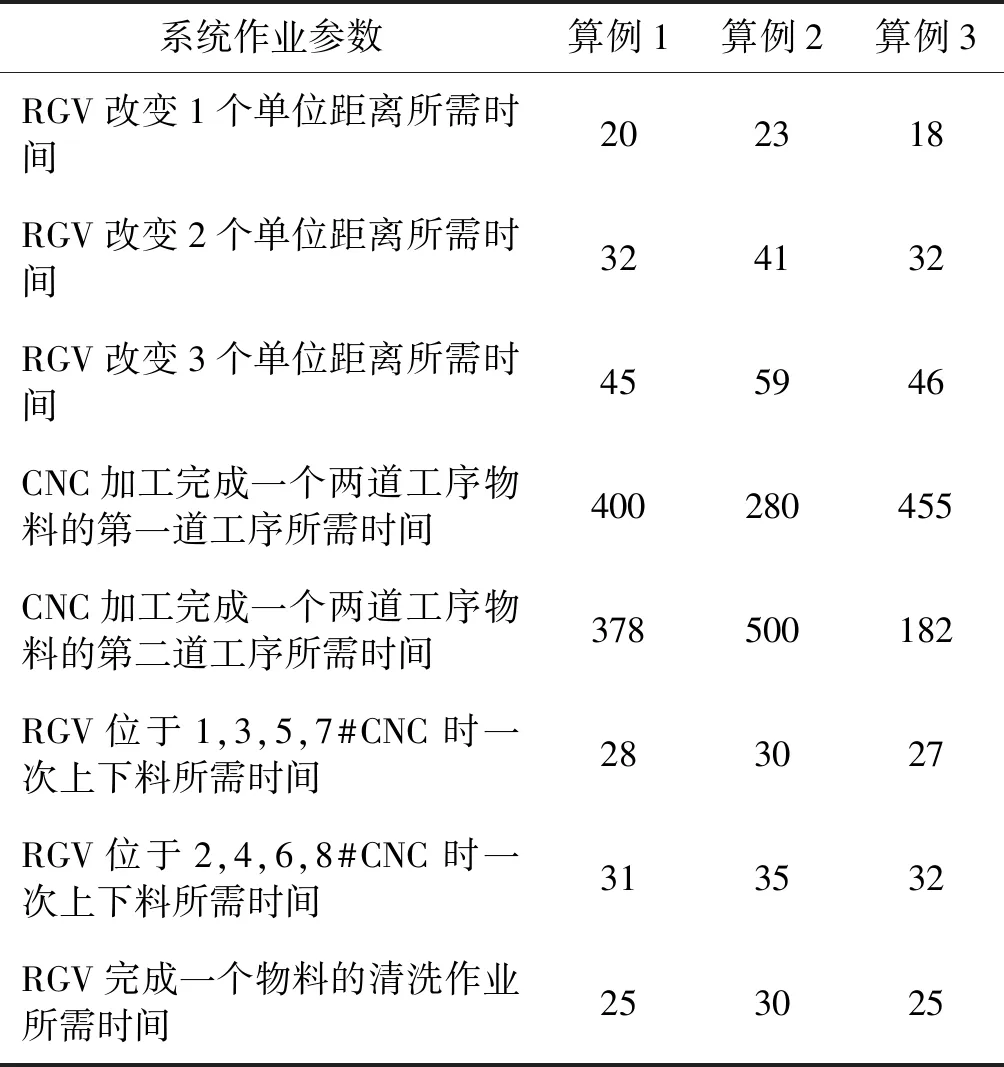
表1 加工系统作业参数 s

其在遗传算法中的参数、加工过程中的参数与稳定性函数中参数的数值定义如表2所示。

表2 参数设置

表中:pm是变异概率；pc是交叉概率；α、β是综合评价函数的两个参数；Errmin、Errmax是机器损坏时间的上下界。

假设一个元件被2台平行机器进行加工，一个加工第一道工序，另一个加工第二道工序。分别假设加工机器为单台加工机器和两台平行放置的机器，故用表1中的数据进行模拟时没有RGV的移动时间，8台机器加工的工件件数与2台机器加工的工件件数之比分别会小于4。为了评价该模型的实用性，2台机器加工设置了4、3、2三个指标，数值越高代表模型实用性较优，数值越低代表模型实用性较差。

表1中所给的三组数据共分为两种情况：情况一为加工第一道工序所需时间大于加工第二道工序所需时间，即算例1、算例3；情况二为加工第一道工序所需时间小于加工第二道工序所需时间，即算例2。两类流水线的示意图如图8所示。

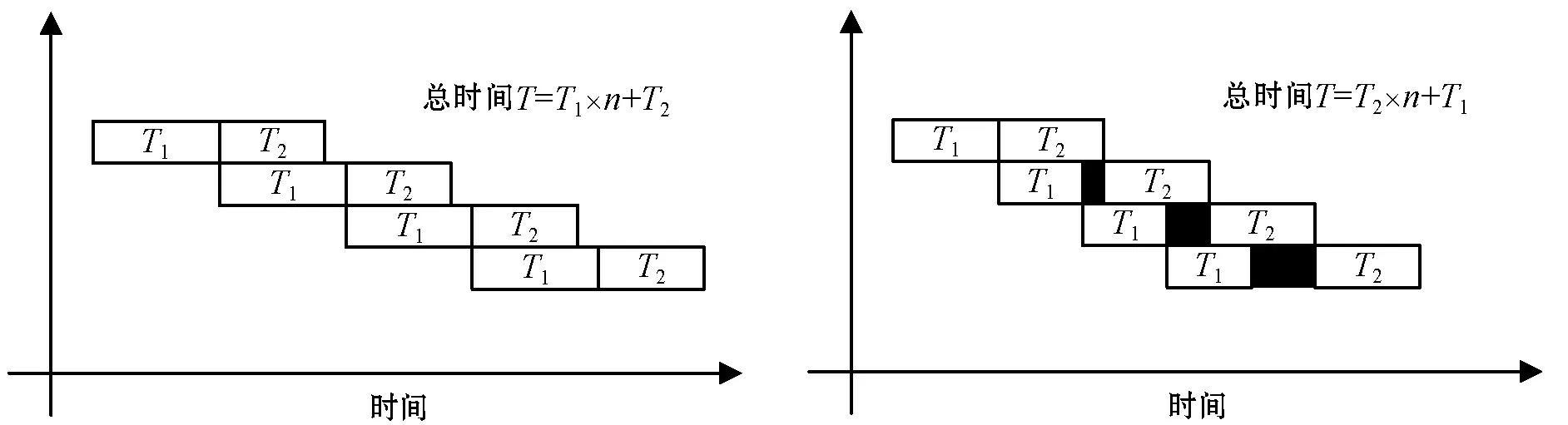
(a)(b)图8 两类流水线的示意图

假定使用2台机器分别加工第一道工序和第二道工序并且平行放置，则加工工件的最大值满足：

(15)

式中：ehk代表数组k中CNC加工第h道工序所需时间；q1k代表数组k中部分CNC一次上下料所需的时间；q2k代表数组k中另一部分CNC一次上下料所需的时间；ak代表数组k中RGV完成一个物料的清洗作业所需时间；e(3-h)k代表数组k中的CNC加工第3-h道工序所需时间，并要求ehk大于e(3-h)k。

以加工150个工件为例，计算8台机器在规定件数下加工所需的时间与只有2台机器时在规定件数下加工所需的时间长度数之比，结果如表3所示。并计算3种算例的平均数表示该模型的实用性，其平均值为3.34。由于作业参数比例越大越好并且其最大值为4，故该模型实用性较好。

表3 加工系统作业参数

同样以加工150件工件为例，对于无故障的加工时间求解来说就是在前面的基础上将故障概率部分都设为0。根据是否使用此调度算法得到了两种调度方案，不使用此调度方案的执行方式是可能在遇到损坏并还未维修完成的机器上仍旧进行加工，其可能导致之后将要加工时出现拥堵现象。对得到的两种不同的带有故障的时间与未带故障时求解得到的时间计算稳定性函数。

由于遗传算法的局限性和故障发生的随机性，一次运算的结果往往不具有代表性，因此本文对大量运算结果进行了处理。

在配置为：Intel i5-6300HQ的CPU，主频为2.3 GHz，内存为16 GB的个人电脑上运行。对每组进行50次重复实验，并求取各算例下不同算法的加工总时间，进一步求取平均值，得到减小每次随机误差后的综合评价值，结果如表4所示。

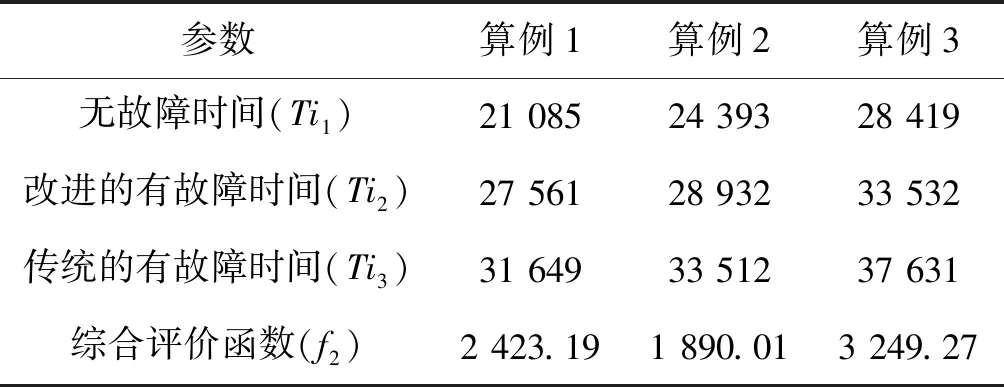
表4 模型的综合评价

将各个算例下不同算法的时间做成折线图，如图9所示。

图9 两类算法的时间对比

综上所述，此模型可以得到一个既满足稳定性高又满足所花时间少的调度优化结构。

4 结 语

本文在研究此柔性作业车间调度问题的相应特点的前提下，提出了解决该问题的多段染色体编码的遗传算法优化算法。该算法对机器选择部分、工序排序部分、故障概率部分和工序选择部分四部分，分别使用了不同的编码方式。多段编码保证了在求解过程中问题解的稳定性与可解性的提升。在实际问题的模型构建中，考虑了对于机器损坏的时间以及机器运动的时间，进而减少了约束条件，保证问题与实际相符合。同时通过使用相应算例对模型进行验证，由数据与对比结果进一步验证了此算法的有效性以及实用性。根据两种调度方案所需时间以及与得到的加工系统作业参数均值为3.34进行对比，进而验证本文所构建模型的实用性较好。

在实际问题中常常会出现机器的损坏，从而给最终结果造成极大的误差。为了避免此类问题的发生，我们引入了综合评价函数，使得最终结果在满足稳定性高的情况下得到数据的最大化。同时更贴近实际生产过程中会出现机器损坏导致作业中断的情况，即可能导致之后将要在损坏并还未维修完成的机器上进行加工时造成拥堵现象。最后通过调度算法有效缓解了该拥堵现象。