变上限积分求导定理课堂教学构思设计及实践效果

杨莉　朱立军

摘  要：变上限积分求导定理是高等数学教学中的难点，如何使本节课有效的进行，授课教师对其进行了精心的构思：提出问题→解决问题→问题总结→拓展探究，在此过程中融入启发式、探究式及团队式教学模式，教学课件丰富，教学语言诙谐，教学互动灵活，教学效果明显。

关键词：变上限积分;求导定理;课堂教学;构思设计

中图分类号：G642         文献标志码：A         文章编号：2096-000X（2020）01-0122-03

Abstract： Variable Upper Bound Integrals Derivative Theoremis the difficulty inCalculusteaching.To make this lesson effective， the teacher carefully designed it by following steps： ask questions，answer questions，summarize questions and expand inquiry. Heuristic， inquiry and team-based teaching modes are adopted in the process， which obtain rich teaching courses， humorous teaching languages， flexible teaching interaction and obvious teaching effects.

Keywords： Variable Upper Bound Integrals; derivative theorem; classroom teaching; conceptual design

《高等數学》是我校理工类和经管类的专业基础课，既能展现基础学科的理论特色又能兼顾专业课程的实践特色，同时也是学生学习其他后继课程的基础，在人才培育中占有重要地位。通过该课程的学习，能很好的培养学生的抽象思维能力、逻辑推理能力、空间想象能力、运算能力以及综合运用所学知识去分析和解决实际问题的能力。

如何提高高等数学的教学质量，已经成为《高等数学》教学活动中亟待解决的课题。对于民族院校经济类专业《高等数学》教学，需考虑学生的生源及个体差异性，对教学过程的设计需精心构思，目的激发学生对高等数学课程的积极性和热爱程度，使其一环紧扣一环的继续学习高等数学后续知识，并且更重要的是在数学课程中培养学生积极正能量的人格品质，从而为少数民族地区培育有用的服务型人才。

变上限积分是高等数学中联系不定积分与定积分的一个重要概念，其教学设计构思关系着整个教学效果的整体呈现。以下为变上限积分教学构思设计过程与实践效果。

一、承前启后，有效导入

全体同学请将你的美丽目光集中在这里（手势右手大展绕一圈指向左手手心，提示大家注意），同学们，早上好！

今天我们一起来探讨学习第6章定积分6.4节微积分基本定理之变上限积分求导定理。

上节课，我们提出了两个问题。

问题1：我们已经系统的学习了一元函数的微分学、初步的学习了积分学，我们要问：这两者之间是否有一定的联系呢？如果有，能说明什么问题？

问题2：截至目前，求定积分只能通过定义，然而定义中的和式极限给计算带来了一定的繁杂性，那么要问：是否有一种更巧妙简便的办法来计算定积分？

为此，我们引入了变上限积分。

通过拉窗帘活动，由已知（定积分）到未知（变上限积分），自然过渡到变上限积分的定义。

进入PPT：

一、变上限积分

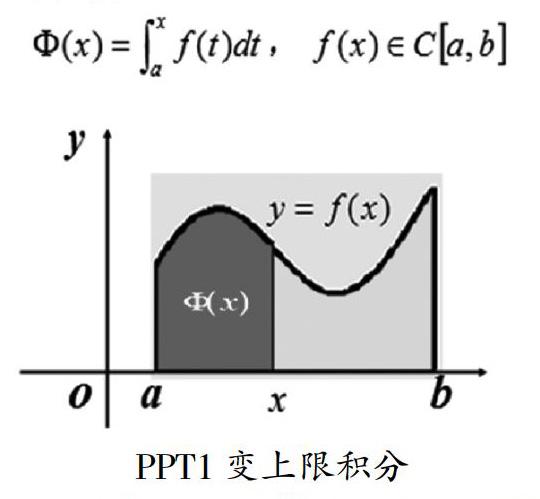
观察这个式子'（x）=f（x），认识一下？椎（x）和f（x）的关系。f（x）是？椎（x）的导函数，？椎（x）是f（x）的原函数。那也就是说在[a，b]上连续的函数f（x）必然存在原函数，下面以定理的形式给出。

PPT4变上限积分求导定理

变上限积分求导定理回答了上节课我们提出的第1个问题微分学与积分学的联系，它是沟通微分学与积分学的桥梁。同时说明了变上限积分的导数等于被积函数在上限处的函数值，也表明了闭区间上的连续函数必然存在原函数，而且这个原函数是由其本身生成的变上限积分函数。

趁热打铁，我们利用定理1求几个变上限积分的导数。

定理1是我们这节课的终极目标，目的达到，课程到此结束。

四、梳理总结，拓展探究

下面我们来简单梳理总结一下本节课。

由上节课提出的两个问题我们引入变上限积分，本节课比较严谨的分析推导变上限积分求导定理。在分析过程中遇到两个有趣的疑难点：

（1）                  复杂问题简单化;

（2）             ，将变量为？驻x→0时的极限转化为变量为？孜→x时的极限，问题简易化。

这也就是说我们在遇到困难时，一种办法行不通，我们得大胆尝试、探索寻求另一种方法来解决，那么我们想要的那个美丽的答案马上会得到。正所谓宋代诗人陆游《游山西村》中的一句诗所说“山重水复疑无路，柳暗花明又一村”。

下面布置作业，课下同学们可以试着完成两个任务。注：课下作业任务2同学们在“学习通”主题讨论中互相讨论;任务3的WORD编辑上传到“学习通”作业（在线课程任务）中。

PPT5课下作业

五、实践效果，问卷呈现

本节课于管理学院选修《高等数学》班级进行，通过对39名学生进行问卷调查（参见文献[5]），整体教学效果良好，抽选问卷（共12个问题）中的4个问题如下。

参考文献：

[1]同济大学数学系.高等数学（第六版）：上册[M].北京：高等教育出版社，2006.

[2]赵树嫄.微积分（第四版）[M].北京：中国人民大学出版社，2016.

[3]肖俊.关于变上限函数求导的教学实例[J].高等数学研究，2013，16（06）：49-51.

[4]变上限积分函数动态图[EB/OL].http：//img.bimg.126.net/photo/KEf5qTFJDxB_ovLzLHL7mQ==/4224376450474286368.jpg.

[5]6.4节微积分基本定理之“变上限的定积分”求导定理教学效果测评问卷调查[EB/OL].http：//mooc1.chaoxing.com/course/202227494.html