一种适用于开采沉陷的InSAR最大可检测形变梯度函数模型

高 建 陈炳乾 冯遵德

（1.江苏师范大学地理测绘与城乡规划学院，江苏徐州221116；2.煤炭资源清洁利用与矿山环境保护湖南省重点实验室，湖南湘潭411201）

合成孔径雷达干涉测量（Interferometric Synthetic Aperture Radar，InSAR）是近年来发展起来的一种新型大地测量手段，该技术能够进行大范围、高精度、低成本和长周期地表沉降监测［1］，很大程度上弥补了传统监测方法的不足，为矿区地表变形监测提供了新方法。尤其是高级InSAR 技术（如小基线集技术、永久散射体技术等）的出现，进一步克服了传统In-SAR技术时空基线的限制，并在一定程度上消除了大气影响，提高了InSAR技术监测矿区形变的精度和可靠性，使InSAR技术成为矿区变形监测的重要手段之一［2-7］。然而，当矿区地表发生大梯度形变时（如地表塌陷），其形变梯度超出InSAR 最大可检测形变梯度（MDDG）时，对应的干涉条纹会发生混叠［8-9］，此时若采用常规解缠算法则无法恢复矿区的真实形变相位。为有效判断InSAR 方法是否适用于地表变形区域探测，减少不必要的人力、物力与财力浪费，一些学者相继提出了InSAR 形变梯度检测模型。其中，Massonnet 等［10］于1998 年首次根据干涉测量的基本条件提出了MDDG 的概念并给出了InSAR 的MDDG理论公式，即为雷达波长的与像素大小的比值［10］。然而在实际InSAR 测量中，由于受时空去相干、大气、噪声等因素的影响，真实InSAR能够检测的MDDG 值远小于理论值。因此，Baran 等［11］于2005 年将相干性引入到MDDG 函数模型中，提出了基于In-SAR 相干性的MDDG 函数模型。在此基础上，蒋弥等［12］对Baran 模型进行改进，引入多视视数作为自变量，基于C 波段的SAR 影像，提出了融合InSAR 相干性和视数的MDDG函数模型。之后，王琪洁等［13］基于L波段的PALSAR数据建立了形式类似的函数模型。

以上函数模型为合理选择变形监测对象提供了有益参考，然而现有模型在实际应用中需要提前获取SAR影像计算相干性或相干性+视数来判断InSAR技术应用的适宜性，并且在应用于矿区开采沉陷时未能考虑矿区开采的实际情况和不同的地质采矿条件对开采沉陷的影响。本研究从煤矿开采引起的地表形变出发，结合开采沉陷的地质采矿影响因素，提出一种适用于矿区开采沉陷的InSAR 形变梯度函数模型。该模型无需事先获取SAR 影像计算相干性，只需利用地质采矿条件参数即可判断不同波长、不同分辨率和不同入射角的InSAR 数据的最大可检测值，其可靠性通过实际矿区的SAR 影像试验进行了验证。

1 影响开采沉陷的地质采矿因素

大量工程实践表明，矿区地表沉陷是自然地质与采矿因素综合作用的结果。自然地质因素包括煤层埋藏的几何条件（如煤层厚度、倾角和埋深等），构造因素（如褶皱程度和断层密度等）和岩石物理、力学和化学性质（如岩石硬度系数和水文地质性能等）［14］。以上因素属于不可控因素，因此本研究在后续建模过程中不予考虑。

影响地表沉陷的另一类主要因素是采矿技术因素，主要包括煤层开采深度、开采厚度、顶板管理方法和采空区尺寸等。现有研究表明：开采厚度越大，垮落带、导水断裂带高度越大，地表移动和变形值也越大；同时随着开采深度的增加，地表各种移动变形值减小，地表移动范围扩大，移动盆地更平缓［15］。地表移动和变形既与开采厚度成正比，又与开采深度成反比，因此开采深厚比可作为衡量开采条件对地表沉陷影响的估计指标［16］。

顶板管理方法决定了覆岩及地表的破坏程度、移动量大小。顶板管理方法有全部垮落法、充填法和煤柱支撑法等［17］。目前，全部垮落法是国内矿区普遍采用的顶板管理方法，因此假定顶板管理均采用全部垮落法，采空区尺寸影响地表的充分采动程度。当采动程度较小时，随着工作面尺寸的增加，地表移动盆地范围内各种移动变形值均增大，当达到充分采动后，工作面尺寸大小对地表移动和变形值大小无影响［18］。工作面尺寸大小对地表移动和变形值的影响规律可以用下沉系数来表征［14］。随着工作面尺寸的增加，采动程度逐渐变大，同时下沉系数逐渐增加，当工作面达到一定尺寸时，地表达到充分采动后，下沉系数趋于定值。因此，本研究将下沉系数作为后续建模的另一参数。

2 研究方法

本研究方法分为数据预处理过程和建模过程。数据预处理的主要目的是确定MDDG 与下沉系数之间的关系，生成初始模型，并探讨SAR 影像参数对两者关系的影响；建模过程是基于预处理中得到的结论来分析初始模型与开采深厚比的关系，从而将开采深厚比引入函数模型，最后选取合适的拟合函数得到最终的函数模型。由于数据预处理过程和后续建模过程的数据处理步骤一致，因此本节将着重阐述数据预处理步骤，如图1所示。

为确定下沉系数与MDDG 的关系，并研究SAR影像参数对两者关系的影响，在开采深厚比不变（所选开采深厚比为150）的前提下，选取不同的SAR 影像参数（波长、分辨率和入射角）和下沉系数进行分析。具体步骤如下：

（1）设置不同的下沉系数，利用概率积分法［19］模拟生成不同量级的形变场。

（2）基于步骤（1）中不同量级的形变场，设置SAR影像的波长、分辨率和入射角，并结合雷达干涉测量基本原理模拟得到对应的差分干涉相位。

（3）采用最小费用流方法对步骤（2）得到的模拟差分干涉相位进行相位解缠。以概率积分法得到的形变相位作为参考，对解缠后的相位进行准确性验证，并提取解缠正确的相邻两像元以计算形变梯度。形变梯度计算公式为

式中，Gradient 为O、P 两点间的形变梯度；ΔO和ΔP分别为两相邻像元O 点和P 点的下沉值；D 为像元间距离。

（4）统计分析步骤（3）获取的可检测形变梯度，得到不同SAR 影像参数（不同波长、不同分辨率）下下沉系数对应的MDDG 值。通过线性拟合分析下沉系数与MDDG值的关系，确定临界下沉系数。

（5）将步骤（4）得到的MDDG 值与临界下沉系数进行第一次回归分析，建立初始函数模型。

（6）预处理过程确定了临界下沉系数与MDDG的关系，排除了SAR 影像参数对初始模型的影响，即模型无需引入SAR参数变量。因此，建模过程中的模拟数据只需以开采深厚比为变量，数据模拟与预处理过程一致。以步骤（5）得到的初始函数模型为基础，探寻开采深厚比与初始模型的关系，并采用经验统计和二次回归分析方法，确定最终的MDDG函数模型。

3 试 验

3.1 数据预处理

本研究所有的模拟数据均在长度400 m、宽度200 m 的模拟工作面上获得，并且为保证矿区变形影响范围能够被完整地模拟，设置SAR 影像区域为1 000 m×1 000 m。采用概率积分法进行形变场模拟，选取的参数如表1所示。

?

3.1.1 数据模拟与分析

现有研究表明［17］：当开采深厚比小于30时，地表极易产生地裂缝、塌陷坑破坏，该地质采矿条件下的形变梯度较大，地表移动和变形在空间和时间上呈现不连续性，且地表变形不具有明显的规律性；当开深厚比大于200 时，地表变形也无明显规律。因此，本研究在保证表1中参数不变的前提下，固定开采深厚比为150，下沉系数在[ ]0.01,0.9 区间内变化，同时下沉系数以0.01为增量模拟生成90个形变场。

为确保所建立的函数模型适用于不同波长、不同分辨率和不同入射角的SAR 影像，模拟试验在将形变值转化为差分干涉相位时，分别选用了常用的C、L 和X 波段对应的不同分辨率、不同入射角等参数，具体参数取值如表2所示。

?

由表2 可知：3 种不同波长、不同分辨率和不同入射角条件下能够对应生成18 种不同SAR 影像参数下的形变相位，因此预处理阶段模拟的90 个形变场可对应生成1 620 幅差分干涉相位图。将差分干涉图经最小费用流解缠得到解缠相位图，以模拟变形转化的形变相位为基准值，规定基准值的为限差，筛选解缠正确的像元并求取像元间的MDDG值。利用经验统计方法分析MDDG 值和下沉系数的数据发现：表2 中每一组参数对应的90 幅差分干涉图（下沉系数变化区间为[ 0.0 1,0.9]），其求得的像元间MDDG 值与下沉系数之间的规律具有相似性，具 体如图2所示。

由图2可知：各个子图虽然选取的SAR影像参数不同，但其MDDG 值与下沉系数的关系在整体趋势上保持一致，即前期MDDG 值随着下沉系数呈线性增长，当MDDG 增大到某一值后，MDDG 将基本保持不变。这是因为：在前期下沉系数较小，地表最大形变值没有超过当前影像参数下的MDDG 值，InSAR 技术能够准确地监测矿区形变；随着下沉系数增大到某一临界值，地表最大形变梯度将等于该影像参数下的MDDG 值，这个临界值可称之为临界下沉系数，即图中的转点处；当下沉系数超过临界下沉系数后，解缠方法只能恢复MDDG 范围以内的像元，此时MDDG值将不随下沉系数发生变化。

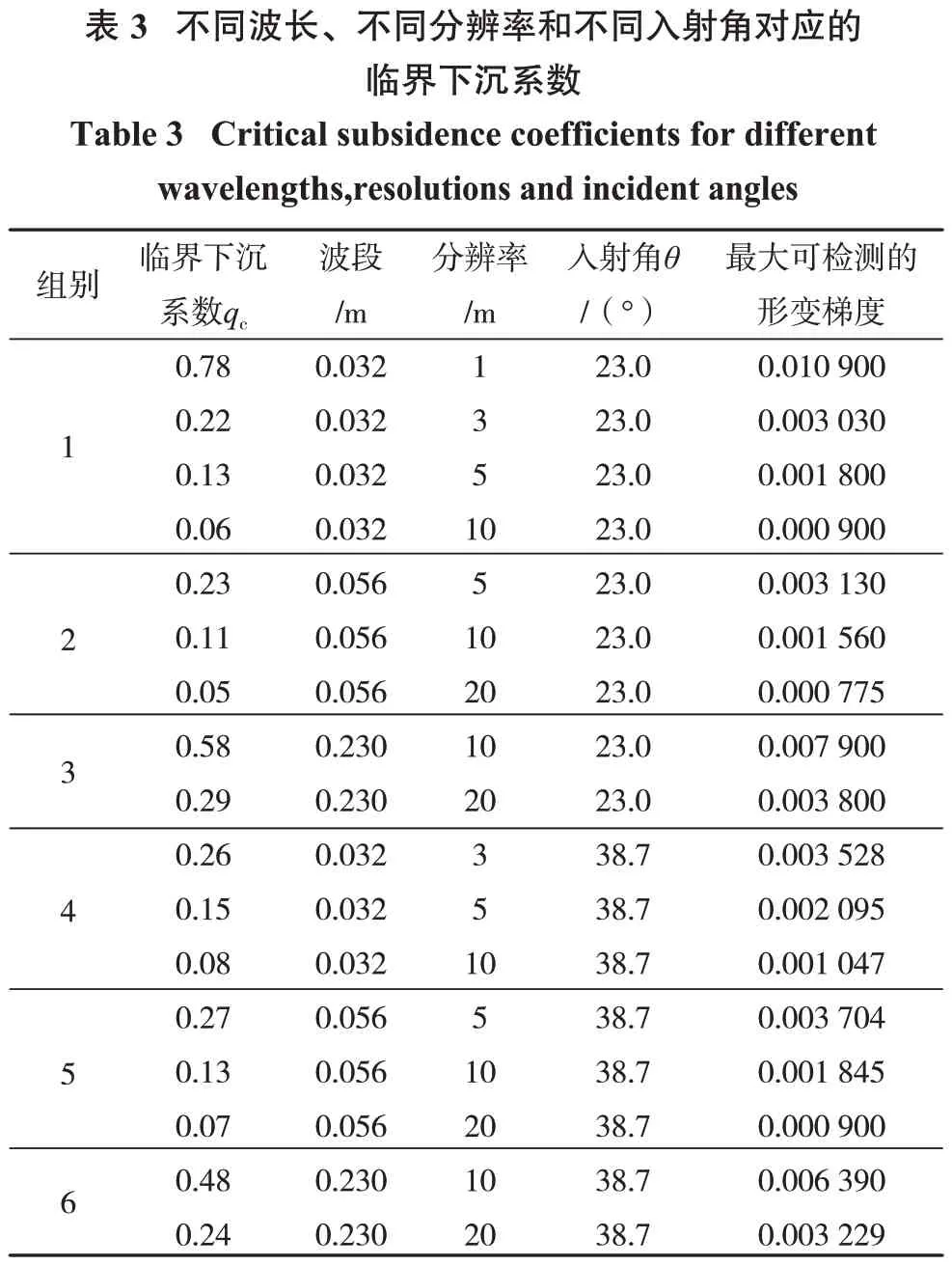
通过以上分析发现，InSAR 技术MDDG 值的求取关键在于临界下沉系数的确定。从模拟数据中提取了与波段、分辨率和入射角相对应的临界下沉系数及其最大可检测形变梯度，如表3所示。

由表3 可知：不同分辨率和波段条件下，临界下沉系数和MDDG 之间具有明显的正相关关系。因此，后续回归分析只需提取出临界下沉系数及其模拟的差分干涉图，即可构建函数模型。

3.1.2 初始模型的生成

为研究MDDG 和临界下沉系数之间的定量关系，并确定波长、分辨率和入射角对两者关系的影响，对表3 中的6 组数据进行了拟合分析，结果如图3所示。

?

由图3 分析可知：MDDG 与临界下沉系数之间存在明显的线性关系，波长、分辨率和入射角不影响MDDG与临界下沉系数之间的关系。

因此，利用表3 中的数据，对MDDG 与临界下沉系数进行了线性回归分析，得到的初始函数模型为

式中，Gmax为最大可检测的形变梯度MDDG 值；qc为临界下沉系数。

式（2）函数模型的均方根误差为9.877×10-5，说明拟合程度极为显著。

3.2 模型构建

为建立开采深厚比和临界下沉系数与MDDG 之间的函数模型，仍以表1 中参数不变为前提，下沉系数以0.01 为增量在[ ]0.01,0.9 区间内变化，开采深厚比以5 为增量在[ 30 ,60 ]区间内变化，共模拟生成了630个不同量级的形变场。

考虑到回归分析的精度问题和数据量冗余造成运算效率不高的问题，在该阶段的形变相位转化过程中去掉入射角38.7°的影像参数，其他参数仍与表2中一致。最终，形变场转化为形变相位的过程相比预处理过程减少了即一个形变场对应9 幅差分干涉相位图），则630个形变场共生成5 670幅差分干涉图。图4展示了不同下沉系数、采深采厚比对应的部分差分干涉图。其中，图4（a）、图4（d）、图4（g）影像参数均为C 波段，分辨率为5 m×5 m；图4（b）、图4（e）、图4（h）的影像参数均为X 波段，分辨率为1 m×1 m；图4（c）、图4（f）、图4（i）的影像参数均为L 波段，分辨率为5 m×5 m。所有影像的入射角θ均为23°。

本阶段对于干涉图处理、模型参数提取和拟合均与预处理过程一致，不再赘述。假设模型为

式中，a为模型系数；b为模型常数。

按开采深厚比的变化，一共拟合得到了7个初始函数模型，模型参数统计如表4 所示。分析表4可知：当开采深厚比在[ 30 ,60 ]区间内变化时，常数b较小，基本在0.000 2左右变化；结合式（3）可知，开采深厚比为150时，常数b量级缩小到原来的1/10。因此，开采深厚比对MDDG 的影响主要集中在系数a，常数b基本可以忽略。故而可将系数a视为有关开采深厚比的函数，即为。为分析系数a与开采深厚比的具体关系，根据表4 数据绘制了如图5 所示的曲线图。

?

由图5 可知：随着开采深厚比的增大，系数a 逐渐减小，系数a 与开采深厚比成反比。由于参数b 与之间并无明显的线性函数关系，且其数值在[ 0.0 00 2,0.000 4 ]区间内小范围变化，因此可进一步分析其变化情况。综上分析，为探究MDDG 与临界下沉系数和开采深厚比之间的关系，其模型可假定为

利用上述模型对模拟数据中提取的临界下沉系数和相应的开采深厚比进行了回归分析，结果如图6所示。由此可得到最终的函数模型为

式中，模型对应的均方根误差为0.000 079 38，说明该模型的准确性显著，符合要求。

4 实例验证

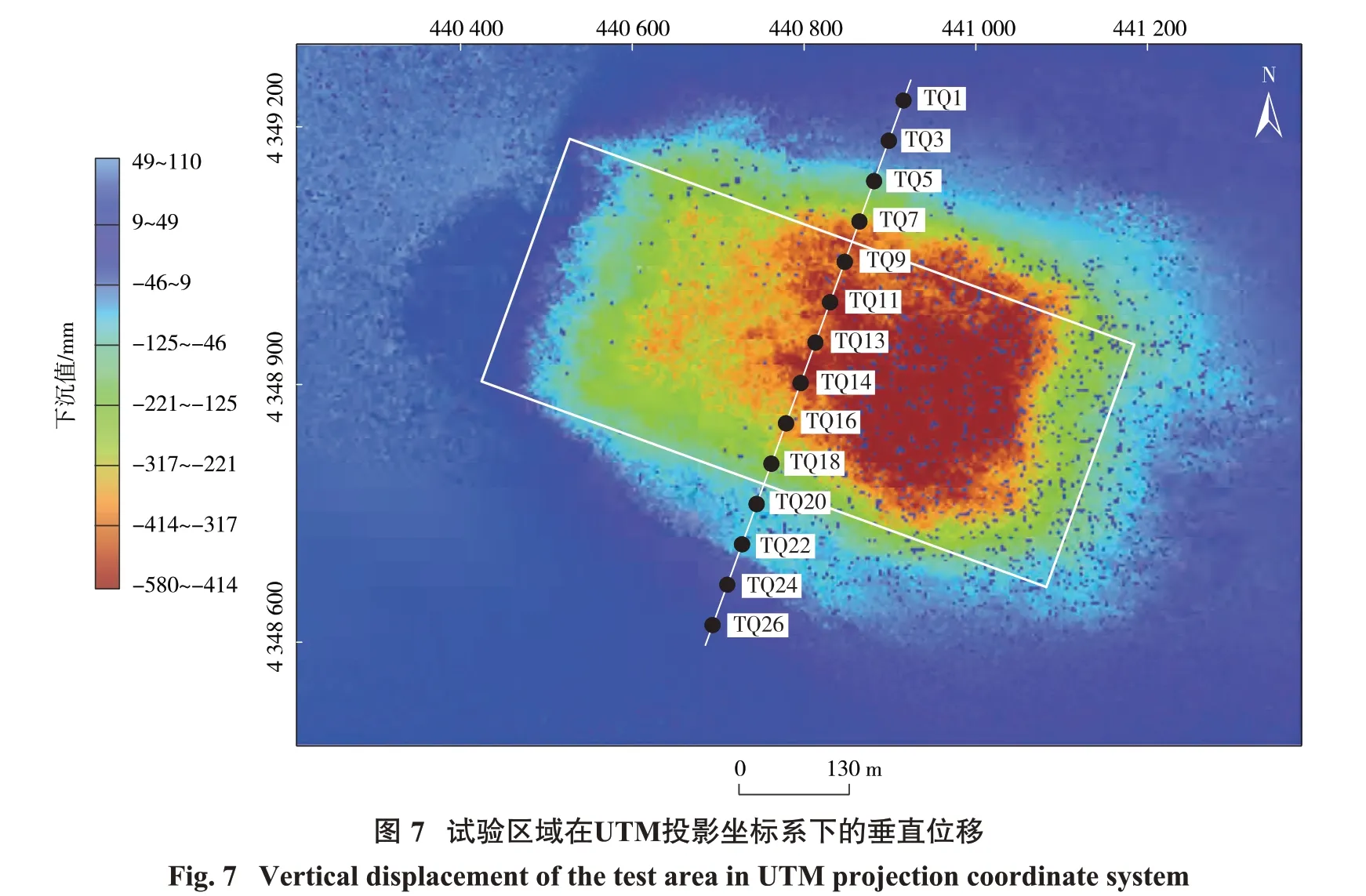
试验区域所在矿区的煤层平均厚度为6.94 m，开采深度为235 m，煤层倾角1°～3°，属于近水平煤层，工作面开采时间为2012 年10 月—2013 年3 月，研究所用的SAR 数据为TerraSAR-X 的High Resolution SpotLight 模式，方位向分辨率为0.85 m，距离向分辨率为0.91 m，时间跨度为2012 年11 月21 日—2013 年4 月2 日，共13 景数据。为获取地表充分采动后的最大下沉值，同时减少时间失相关对SAR 影像的影响，采用文献［20］方法，按时间先后顺序依次对13 景数据进行了干涉组合，生成了12组干涉对，之后对所有组合的干涉对进行叠加获取其总形变量，最终得到的垂直位移如图7 所示。此外，选用地表观测站的GPS 数据作为参考形变值检验所建立模型预计结果的准确性。

由图7 可知：矿区边缘位置条纹清晰，但在工作面中心由于变形较大发生干涉条纹混叠，条纹模糊无法分辨，该区域无法反映矿区真实形变信息。根据临界下沉系数定义并结合研究区工作面参数（开采深度235 m，煤层厚度6.94 m），通过模拟获得该工作面的下临界沉系数为0.14。利用式（5）求得在该时间段内InSAR 的MDDG 值为0.008 56。由于观测线的控制点以20 m 为间隔进行布设，因此根据模型分析结果可知，InSAR 技术在相邻控制点间能够检测的形变量不超过0.171 2 m。

为验证上述分析结论，提取的工作面地表控制点的GPS 点间监测差值如图8（a）所示。由图8（a）可知：在模型预计结果内点间形变梯度有5个部分。第1 部 分 包 括 TQ1～TQ2、TQ2～TQ3、TQ3～TQ4、TQ4～TQ5；第2 部分包括TQ6～TQ7、TQ7～TQ8；第3 部分在矿区中心区域，包括TQ12～TQ13、TQ13～14；第4部 分 包 括TQ19～TQ20、TQ20～TQ21；第5 部 分 包 括TQ22～TQ25。根据模型定义，当控制点两侧形变梯度小于MDDG时，该位置的变形能被InSAR技术有效监 测。故 分 别 选 取TQ1～TQ3、TQ7、TQ13、TQ20、T23～T25作为模型验证对象。为此，分别提取的地表控制点的InSAR和GPS监测值如图8（b）所示。

图8（b）显示：在控制点TQ1～TQ3 部分，InSAR 与GPS 监测结果相近，最大误差不超过0.083 m；控制点TQ7 处监测失真，误差达到0.272 m；控制点TQ13 处监测失真，误差超过3 m；控制点TQ20 处监测有效，误差为0.021 m；在控制点TQ23～TQ25 部分，GPS 和InSAR监测值基本吻合，相差最大不超过0.019 m。

由此可以看出，模型对连续点的检测能力较强，如：TQ1～TQ3这3个相邻控制点的点间形变梯度都在检测区域内，表明检测结果可靠。而当孤点处于检测区域内时，检测精度受到影响，如TQ7、TQ13 点都是这种情况。但有一个特例TQ20 点，其检测精度达到0.021 m。为分析其原因，将TQ7、TQ13 点与TQ20点的相邻点进行对比，发现TQ21～TQ22 点间的形变差值接近0.171 2 m，误差为9.8 mm，可称为近检测点；对于TQ7和TQ13两点，其相邻点的点间形变差值与0.171 2 m 的误差均达到分米级以上，说明这两点均为远检测点。因此可以判断：若孤点的相邻控制点为近检测点时，模型检测精度也会提高。综合上述分析可知，本研究模型对连续点或相邻控制点为近检测点的孤点有较高的检测能力。

此外，进一步利用蒋弥等［12］提出的形变梯度模型与本研究模型进行对比试验。采用文献［12］中的计算方法得到的矿区形变梯度为0.014 29，然后将SAR 影像多视比例设置为1∶1，利用生成的相干图计算出矿区相干均值为0.385。根据蒋弥模型［12］，该矿区在相干系数—形变梯度坐标系中的位置即为图9中五角星符号所在区域。图9 中阴影区域即为模型所求的可检测区，显然矿区的相干性与形变梯度无法采用InSAR技术进行有效检测。

通过与蒋弥模型［12］的对比试验可以发现，本研究模型克服了SAR 影像源和相干性的限制，能够在影像获取前提前计算出InSAR技术的矿区可检测值。同时，该模型精度优于蒋弥模型［12］，能够细化到判断任一控制点的可检测性。

5 结 论

（1）利用数值模拟与回归分析方法，分析了地质采矿因素与InSAR 技术可检测的最大形变梯度之间的关系，建立了适用于开采沉陷的InSAR最大可检测形变梯度模型。利用真实矿区的SAR 影像数据，将所提出的模型与已有模型进行了对比试验。结果显示：该模型无需提前获取SAR 影像，也无需计算SAR影像的相干性，只需利用开采深厚比和下沉系数两个参数即可预计不同开采深厚比、不同下沉系数条件下的不同波长、不同分辨率和不同入射角的InSAR数据的最大可检测值，此外该模型具有较高的预计精度，较强的细化水平，对于促进InSAR 技术在矿区开采沉陷监测中的应用有一定的参考价值。

（2）所建立的函数模型是在保证矿区煤层倾角为0的条件下获得的，且该模型仅考虑开采稳定后的变形情况，没有考虑动态开采过程中InSAR技术的可适用性，这将对该模型的应用造成一定的限制。因此，不同倾角煤层下的InSAR可检测函数模型的建立将是下一步的研究方向。