基于Matlab的山区急倾斜煤层开采沉陷预计系统

赵 博 梁乃森 吴 初 武 雄

（中国地质大学（北京）水资源与环境学院，北京100083）

煤层开采引起的地表移动变形与地表倾角大小、地形条件密切相关［1-4］。不同的煤层倾角、地形条件适用于不同的开采沉陷预计方法［5-7］，为计算方便，通常借助不同的计算机编程语言开发出多功能的可视化开采沉陷预计系统［8-10］，也有学者将机器学习算法应用于开采沉陷预计方面［11-12］。近年来，对于急倾斜煤层开采引起的地表移动变形规律和预计方面的研究，成果丰硕［13-16］，但对于山区条件下的急倾斜煤层开采引起的地表移动变形预计方面的研究深度稍有欠缺［17-18］。相关研究表明［7］：皮尔森Ⅲ型公式法适用于平地条件下急倾斜煤层开采地表移动变形预计，山区地表移动预计模型主要适用于山坡平均坡度小于30°的水平和缓倾斜煤层开采条件下的地表移动变形预计。本研究将皮尔森Ⅲ型公式法与山区地表移动预计模型［7］进行叠加，实现优势互补，在Matlab平台上开发预计系统，对山区急倾斜煤层开采沉陷进行预计。

1 系统设计及编程实现

本研究开采沉陷预计系统分为五大模块，即坐标转换、山地地表曲面拟合、地面移动变形计算、地面移动变形绘图、地表任意点移动变形值计算，通过代码编写、整合及界面开发，便于人机交互操作，实现数据的快速处理与分析。

1.1 计算原理

本研究系统开发是建立在对皮尔森Ⅲ型公式法和山区地表移动预计模型叠加的基础上，因此实现两者参数意义匹配较为重要。通过对公式分析可知，两者参数匹配不存在重大矛盾，皮尔森Ⅲ型公式法可直接应用，将山区地表移动预计模型坐标方向和部分参数意义与前者调整对应即可。

皮尔森Ⅲ型公式法的倾向主断面预计公式为［7］

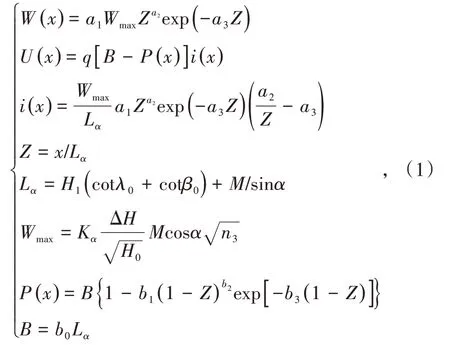
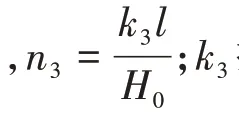
皮尔森Ⅲ型公式法采用的走向主断面概率积分法公式［19］如下：

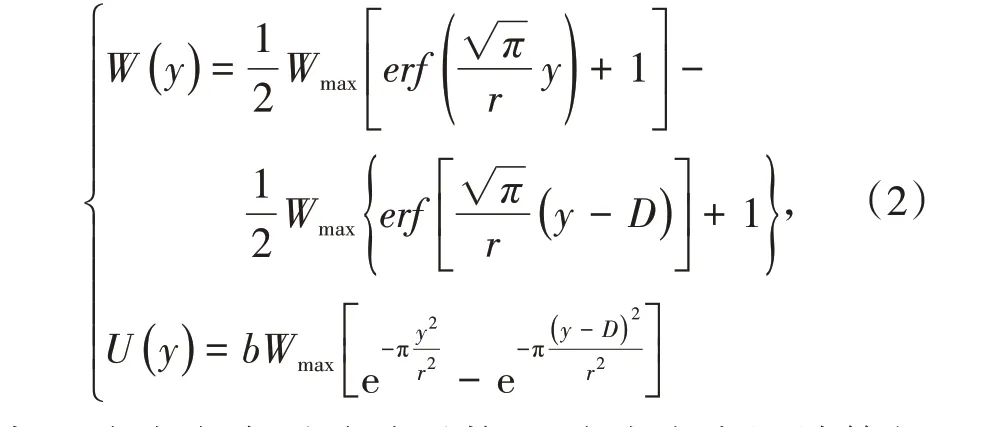
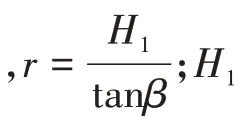
水平地面任意点( x,y )的下沉值W( x,y )和沿φ方向的水平移动值U( x,y)φ的计算公式为［7］

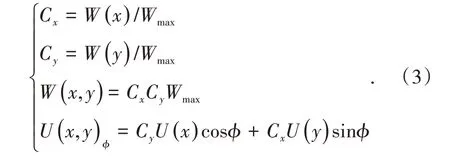
已进行参数调整的山区地表移动预计模型［7］计算公式为

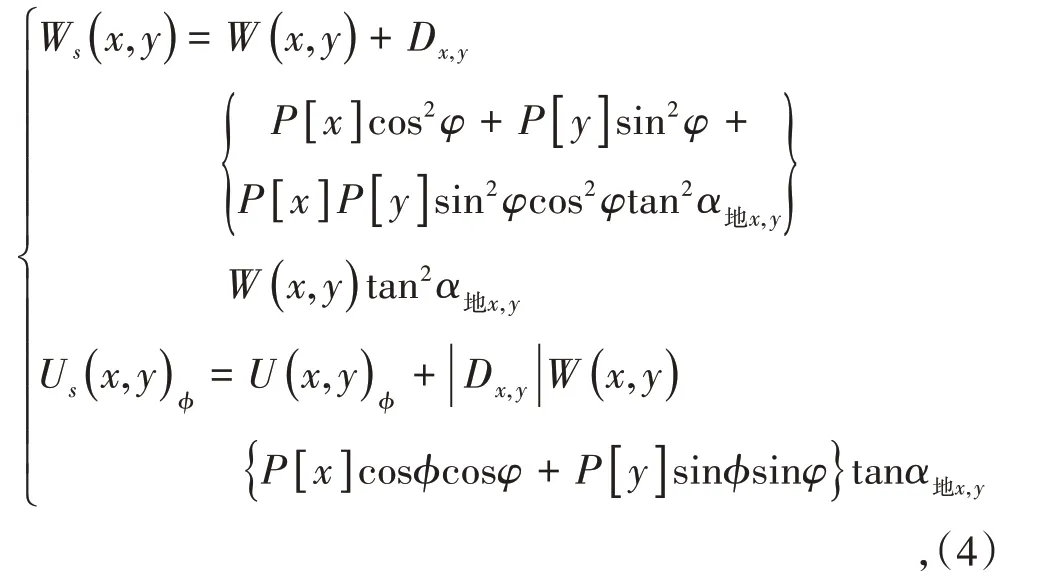
式中，W( x,y)、U( x,y)φ分别为相同地质、开采技术条件下，水平地面任意点( x,y )的下沉量和该点沿φ方向的水平移动量，按式（3）计算，m；Ws( x,y)、Us( x,y)φ分别为叠加山区地表移动预计模型后最终的下沉值和水平移动值，m；Dx,y为点( x,y )的地表特性系数，根据地表类型（表层土与地面植被特征、地貌）取值；α地x,y为点( x,y )的倾角，（°）；φ为点( x,y )的倾斜方向角，（°）；φ为计算方向角，（°）；φ、φ由x轴正向按逆时针方向计算；P[ x]、P[ y ]分别为倾向和走向主断面的滑移影响函数，按下式计算：

式中，S 为工作面倾向方向的计算长度，即倾向主断面下沉盆地全长，m；L 为工作面走向方向的计算长度，即走向主断面计算长度，m；Wm为理论最大下沉值，参考皮尔森Ⅲ型公式法计算，m；A、p、t 为滑移影响参数，参考值分别为2π、2 和π；r 为主要影响半径，计算公式为

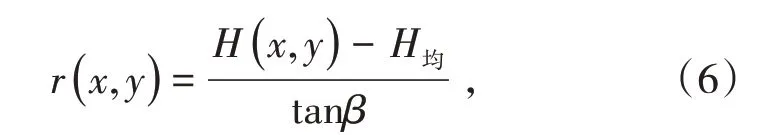
式中，H( x,y )为地表点( x,y )的高程，m；H均为工作面底板平均高程，m；tanβ为主要影响角正切。

1.2 系统开发

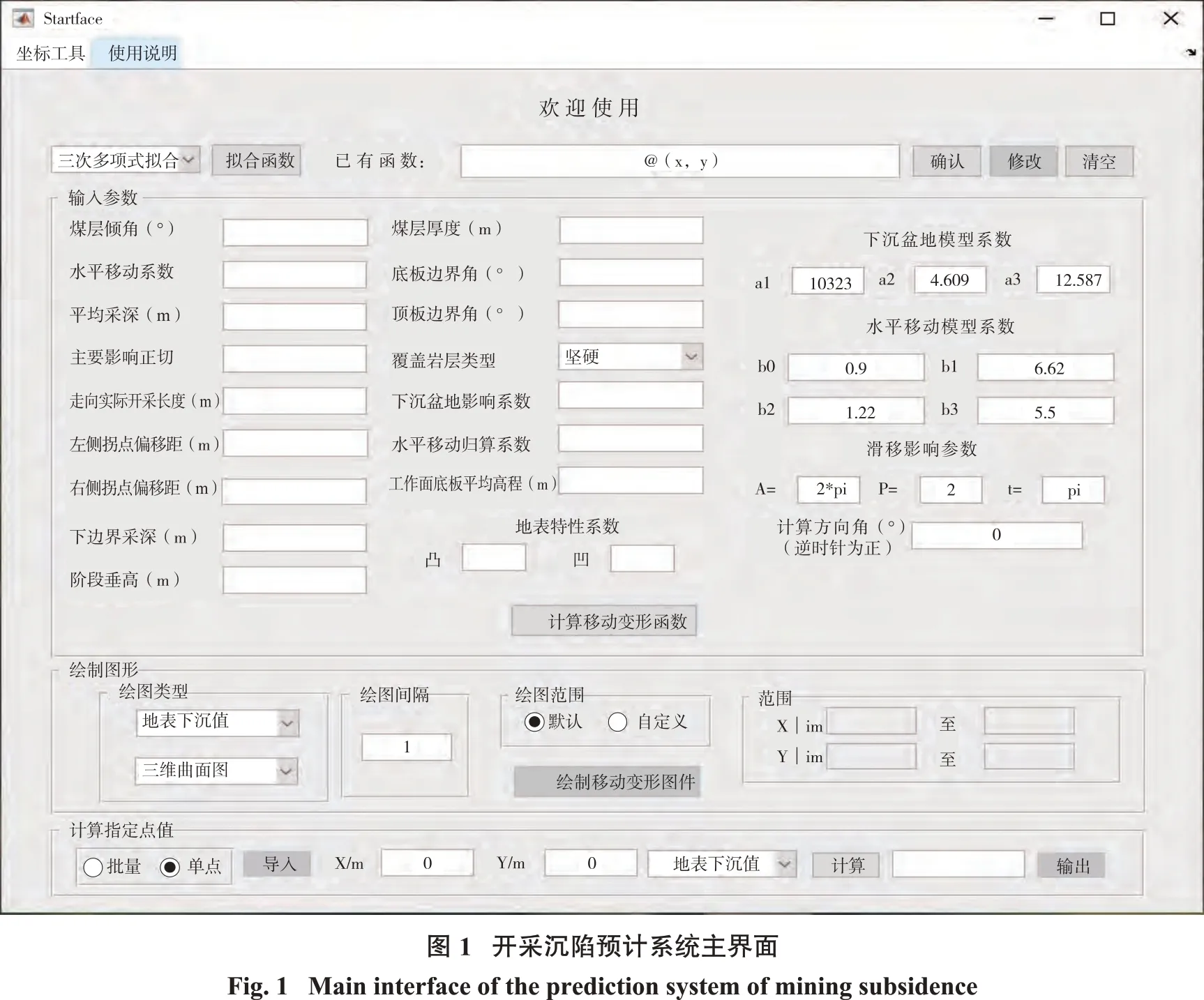
结合皮尔森Ⅲ型公式和山区地表移动预计模型的特点，本研究在Matlab 环境下设计了山区急倾斜煤层开采沉陷预计系统，系统主界面如图1 所示。

1.2.1 统一计算坐标系

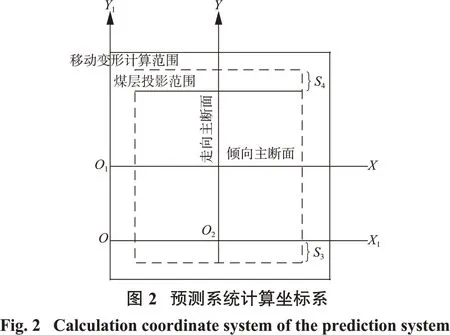
如图2所示，皮尔森Ⅲ型公式法的原始坐标系分别为倾向O1X 与走向O2Y 两个单轴坐标系，为符合平面计算习惯，系统统一计算坐标系为由原始主断面坐标系中O1X 与O2Y 分别向下、向左平移至O1、O2重合形成新的坐标系X1OY1，方便理解计算，本质上没有改变任何变量，其中S3、S4为工作面走向左、右拐点偏移距。

1.2.2 坐标转换工具箱

如图3所示，工作面的计算坐标系根据煤层产状而定（X2OY2），既有的经纬度及高程数据或投影直角平面坐标系以正东、正北为轴（X1OY1），因此需要将后者进行坐标转换以匹配前者，方便计算。若后者为经纬度数据，工具箱将会自动按照经纬度与实际距离长度（m）的换算关系进行近似换算。

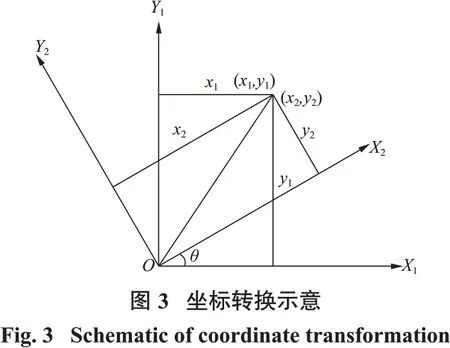
坐标轴旋转公式为

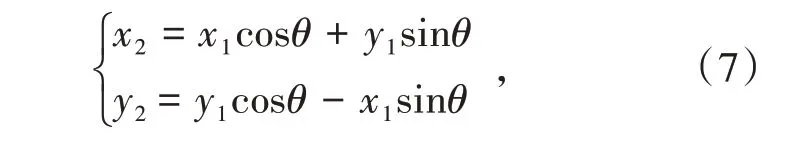
式中，x1，y1为原始坐标，x2，y2为坐标轴绕原点逆向旋转θ角后的坐标。

1.2.3 山区地表曲面函数拟合

山区地表移动预计时需要对坡面任意点的倾斜方向角、倾角、地表特征等进行取值，但由于地貌特性不一，人工取值的数据量巨大，难以实现。本研究对采集的地表三维数据利用Matlab 软件的fit 函数进行多项式拟合，利用高程数据拟合出二元曲面函数方程，模拟山区的地形起伏形态，便于后续计算；利用三维向量夹角计算方法计算坡面任意点倾斜方向角和倾角，通过判断任意点的凹凸性从而给定地表特性系数值。Matlab软件中fit函数提供有三次、四次和五次多项式拟合方法，在本研究系统中分别对应的地形复杂程度为简单、一般、复杂，主要参考地形相对高差、起伏复杂程度进行选择。

部分函数代码如下（“%”之后为代码释义）：

C=importdata（［path，file］，'，'）；%将X，Y，Z格式的三维高程数据文本导入

X=C（:，1）；

Y=C（:，2）；

Z=C（:，3）；

f=fit（［X，Y］，Z，'poly55'）；%利用fit函数将三维数据进行五次多项式拟合

syms x y；%定义x和y符号变量

z=f.p00+f.p10.*x+f.p01.*y+f.p20.*x.+f.p11.*x.*y+f.p02.*y.+f.p30.*x.+f.p21.*x..*y+f.p12.*x.*y.+f.p03.*y.+f.p40.*x.+f.p31.*x..*y+f.p22.*x..*y.+f.p13.*x.*y.+f.p04.*y.+f.p50.*x.+f.p41.*x..*y+f.p32.*x..*y.+f.p23.*x..*y.+f.p14.*x.*y.+f.p05.*y.+f.p23.*x..*y.+f.p14.*x.*y.+f.p05.*y.；%根据函数对象f 的属性（f.p00 等）获取系数值并生成曲面符号函数。

H=matlabFunction（z）；%将符号函数转换为匿名函数，即地表拟合函数，为山区地表任意点的倾斜方向角、倾角计算提供方便.

1.2.4 地面移动变形函数计算

地表移动变形函数计算是整个系统实现中最重要的部分，该模块将上述提及的各计算公式进行耦合编程，在上一模块地表函数拟合完毕后，利用曲面函数和手动输入的计算参数生成各个移动变形预计函数，为下一模块移动变形图绘制提供计算基础，图4所示为主要计算流程。

1.2.5 皮尔森Ⅲ型公式法

皮尔森Ⅲ型公式法主要由三部分组成：倾向主断面计算、走向主断面计算、地面任意点计算。倾向主断面计算依据式（1）以匿名函数进行计算，走向主断面计算依据式（2）概率积分法以匿名函数进行计算，地面任意点计算依据式（3）将前两者组合而成，现仅给出下沉值和水平移动值函数计算代码。

倾向主断面下沉值与水平移动值函数部分代码如下：

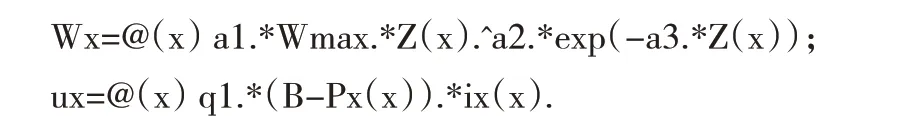
走向主断面下沉值与水平移动值函数代码如下：

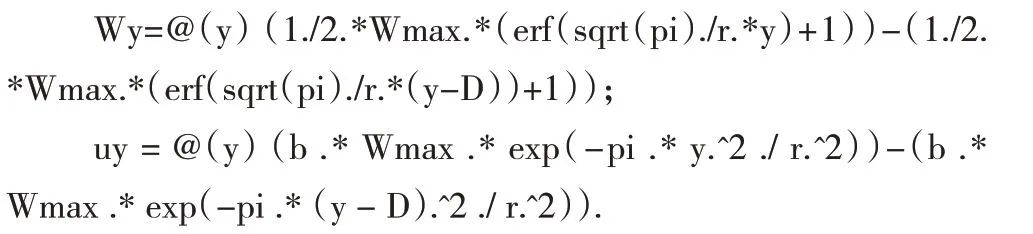
地面任意点下沉值与水平移动值函数代码如下：

syms x y；

Cx=Wx（x）./Wmax；

Cy=Wy（y）./Wmax；

w=Cx.*Cy.*Wmax；

u=Cy.*ux（x）.*cosd（Phi）+Cx.*uy（y）.*sind（Phi）；

Wxy=matlabFunction（w，'Vars'，［x y］）；

uxy=matlabFunction（u，'Vars'，［x y］）；%由Wxy 与uxy 即得到平地急倾斜煤层开采地表移动值任意点的匿名计算函数。

1.2.6 山区地表移动预计

由上述分析得到了地表曲面拟合函数，利用曲面法向量与X 轴和Z 轴的方向向量夹角计算方法，可以得到公式所需的坡面任意点的倾斜方向角和倾角，以此来代替对地表坡面的数据采集。

曲面法向量采用偏导数计算得到，程序代码为

syms x y

vx=matlabFunction（-diff（H，x），'Vars'，［x y］）

vy=matlabFunction（-diff（H，y），'Vars'，［x y］）

vz=1.

坡面任意点的倾角计算代码为

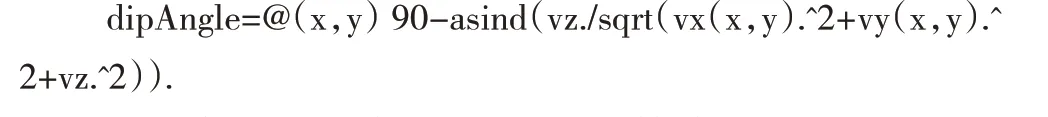
坡面任意点的倾斜方向角计算代码为

dirAngle=@（x，y）Angle（x，y，vx，vy）；

function dirAngle=Angle（x，y，vx，vy）

if vy（x，y）＞0 %用于判断倾斜方向角与x轴正向逆时针旋转夹角是否大于180度

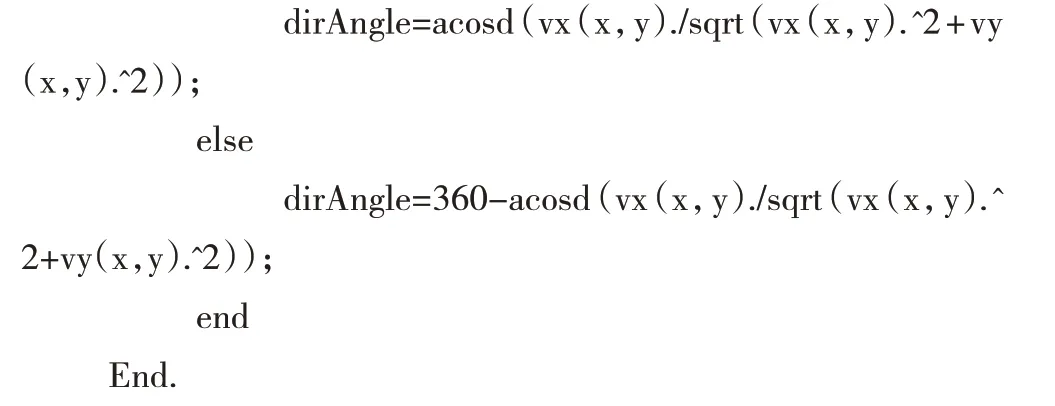
地表特性系数在凹凸处不同，根据曲面函数可计算任意点的凹凸性从而对该点赋值，计算函数为SurfaceValue( x,y)，可在任意点获取对应值。

最后，山区地表移动预计模型[ 式 (4)]与皮尔森Ⅲ型公式法[ 式 (3)]叠加得到最终计算函数，下沉值与水平移动值计算的函数代码如下：

曲率值、水平变形值、倾斜值等函数计算可采用对函数Ws 或us 求导的办法得出。至此，根据所需要输入的参数类型在系统用户界面输入相应的数值，点击“计算”便可得到山区急倾斜煤层开采地表移动变形函数。

1.2.7 地面移动变形图形绘制

在完成了地面移动变形函数计算后，本模块“计算”按钮自动开启，可对地表下沉值、地表水平移动值、地表倾斜值、地表曲率值、地表水平变形值等进行二维及三维图形绘制。为控制图形绘制精度和时长，系统默认绘图采样间隔为1 m，随着绘图间隔增大，绘图时长减小。默认绘图范围由上一模块函数计算时自动生成，可在系统默认的绘图范围内进行修改。

根据绘图采样间隔可得计算坐标列表并生成网格采样点，可将网格点直接代入函数即可得到对应网格点上的地表移动变形值，程序代码为

x=Xmin:interval:Xmax；%interval为采样间隔

y=Ymin:interval:Ymax；

［X，Y］=meshgrid（x，y）；

Z=Ws（X，Y）；

Z=us（X，Y）.

根据得到的X,Y,Z 值，便可通过图形绘制函数生成对应的二维或三维图形，代码为

surf（X，Y，Z，'EdgeColor'，'interp'）%三维图形

contour（X，Y，Z，v，'ShowText'，'on'，'LabelSpacing'，6000）%平面等值线图。

1.2.8 地表任意点移动变形值计算

本研究开采沉陷预计系统可对计算范围内任意点的地表移动变形值进行计算和查询，可以单点查询或批量查询，单点查询直接输入相应点位的( )x,y坐标，批量查询时可导入点位( )x,y 坐标的txt文档，选择计算值类型，点击“计算”。单点查询时可以直接显示，批量查询时则输出为新的txt文件。

2 实例分析

根据甘肃省某矿区山区地下急倾斜煤层开采参数，采用本研究预计系统（登记号：2019SR0590923）对其进行地表移动变形预计和分析。

2.1 预计参数

该采区共有上下两层煤，矩形工作面采用综采放顶煤开采方法，煤层厚度分别为7.2～8.2 m 和29.87～44.82 m，平均厚度分别为7.7 m 和35.6 m，工作面走向长800～1 200 m，煤层平均倾角为52°～53°。根据实际矿区开采和观测资料分析，结合“三下”开采规范［7］中提供的地表移动经验参数值，确定的本研究开采沉陷预计参数如表1所示。

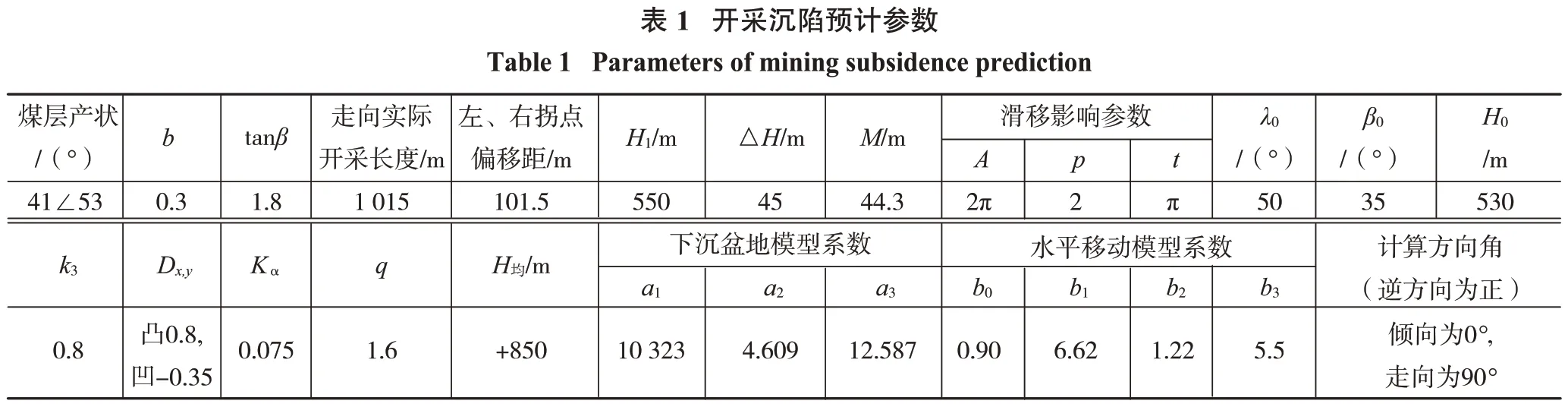
注：Kα、a1、a2、a3、b0、b1、b2、b3等参数参考文献［7］取值。

2.2 开采沉陷预计

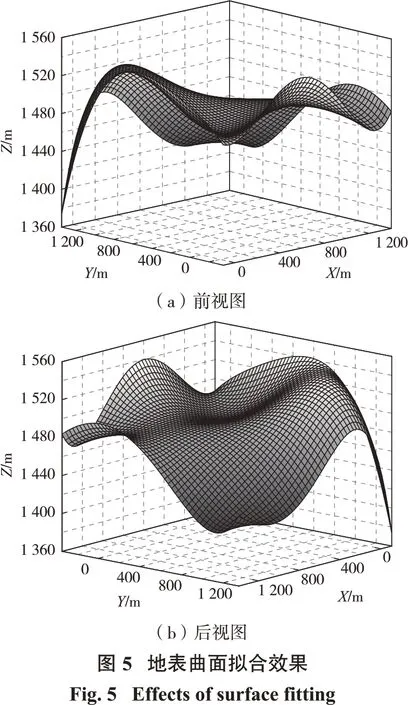
根据计算原点和采区范围将研究区的地表三维高程数据转换为符合系统统一坐标系的数据格式，而后通过Matlab 的fit 函数对该地区复杂地形进行五次多项式曲面拟合，拟合效果见图5。

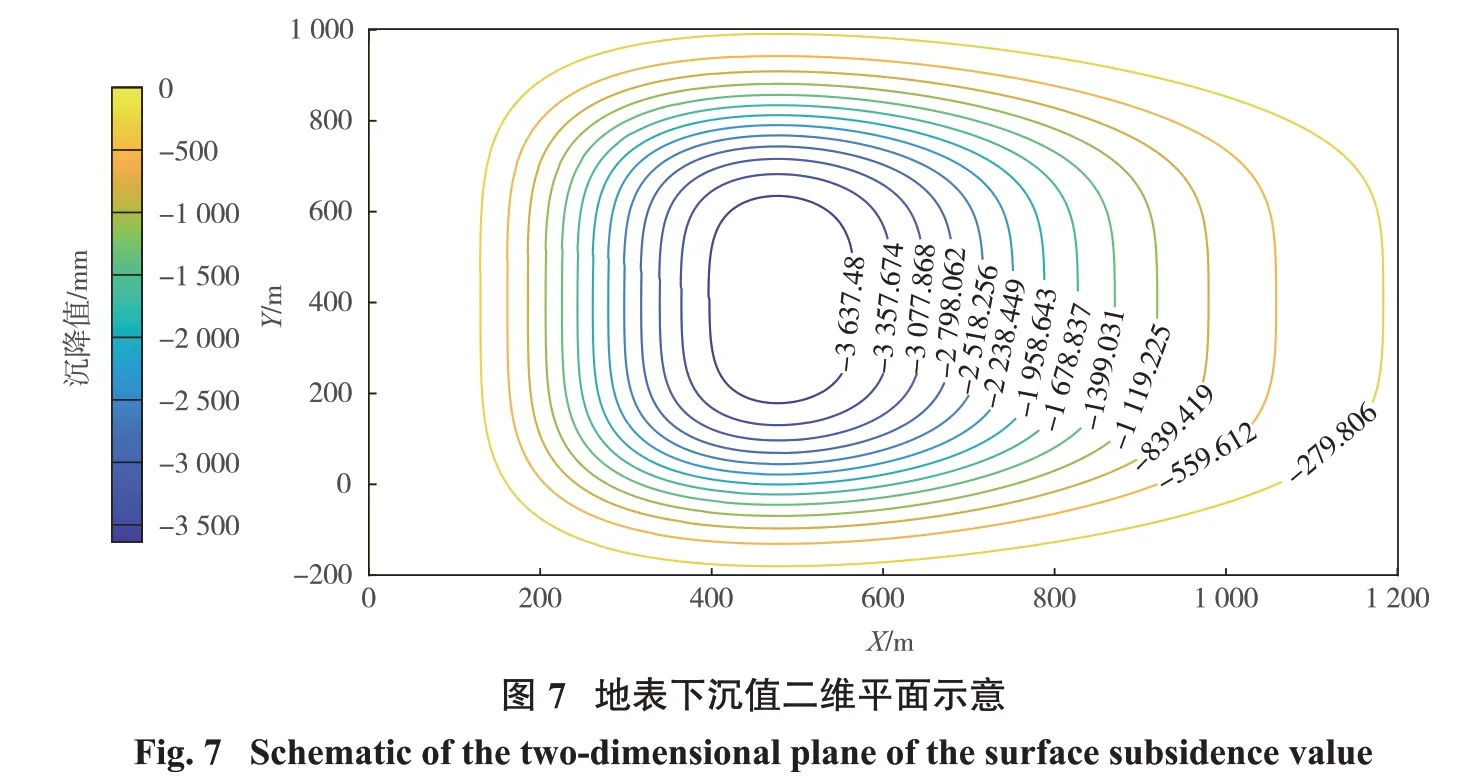
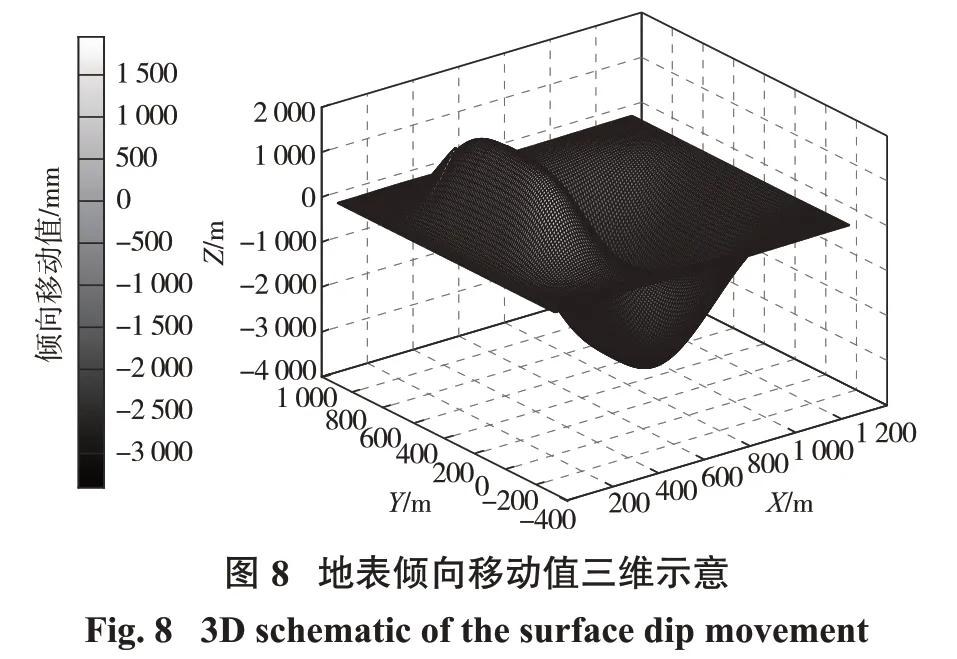
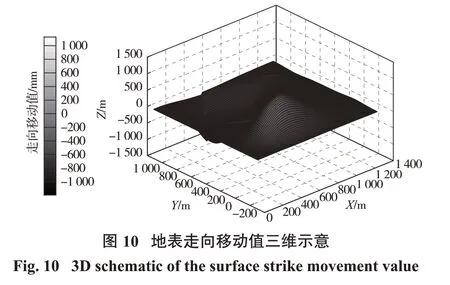
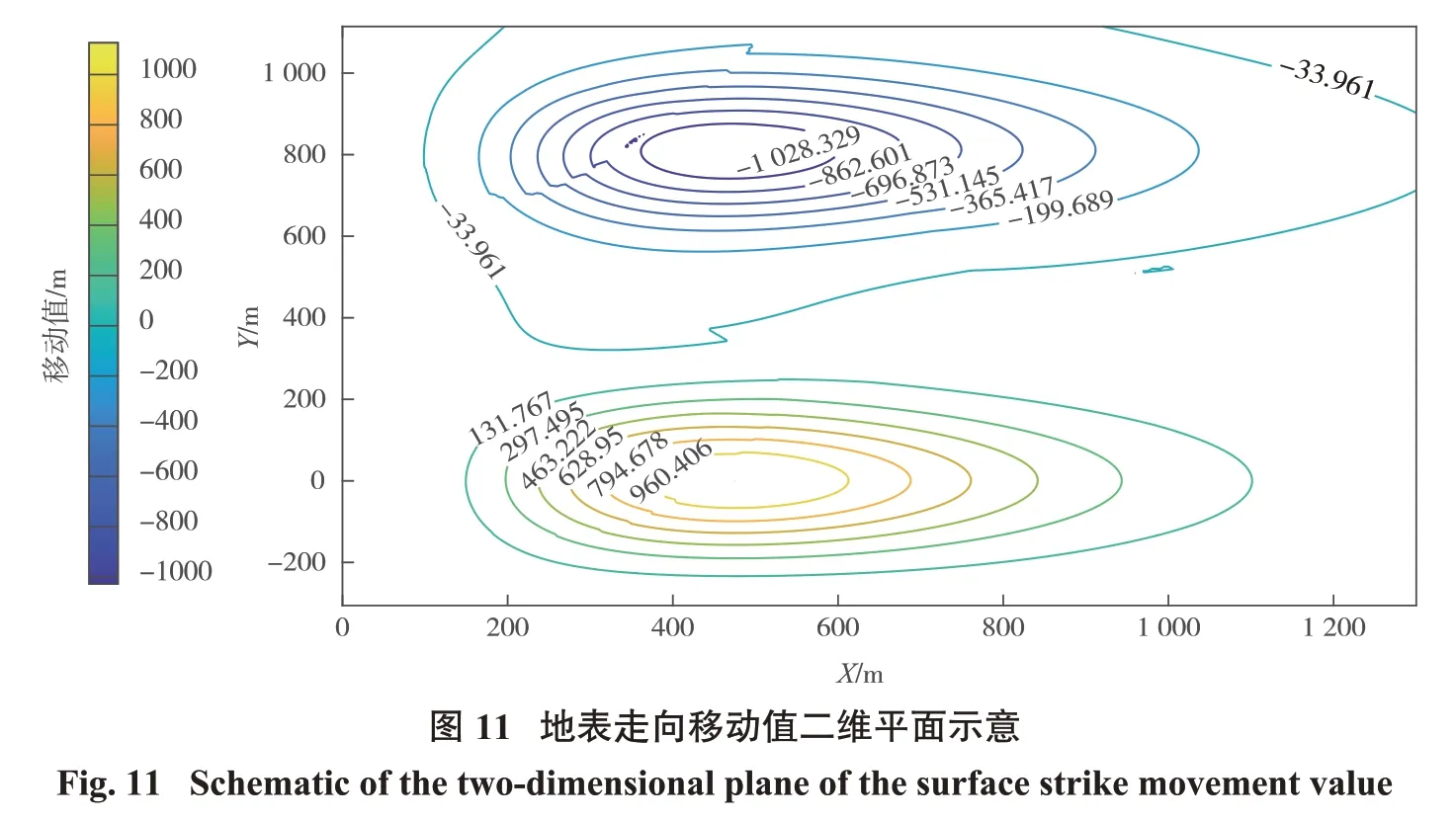
根据地表曲面拟合函数和预计参数进行地表移动变形函数计算并绘图，由本研究预计系统绘制的地表下沉值的三维、二维平面图如图6、图7 所示，绘制的地表倾向、走向移动值的三维、二维平面图见图8～图11。

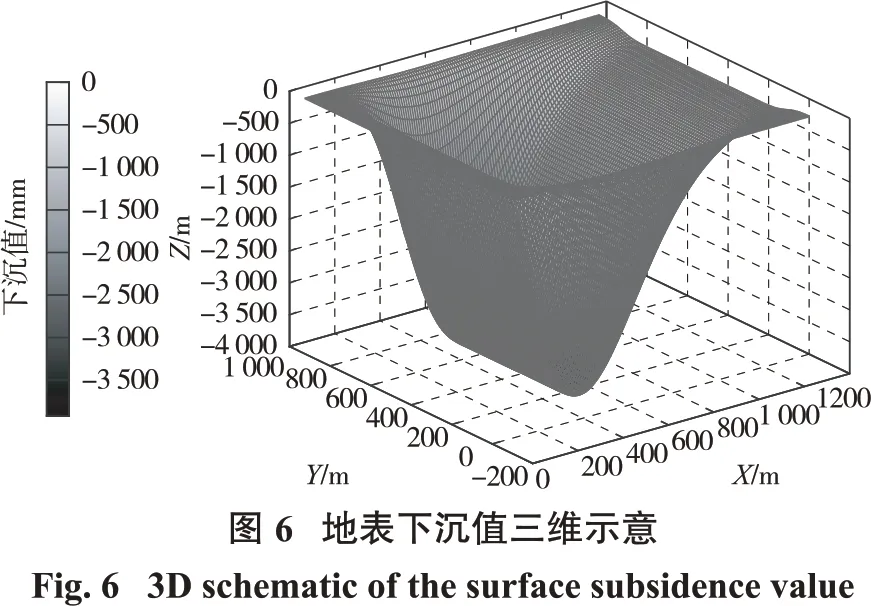
通过观察地表下沉值图形可看出等值线仅有轻微折曲现象，等值线表现较规则，整体来看地表下沉值受山区条件的影响较小；对地表倾向、走向移动值图形观察发现，等值线出现明显的折曲变化，尤其对于走向移动方向的影响较强，而对于倾向方向移动影响较弱，反映出水平移动值受山区条件的影响较大。

2.3 数据验证分析

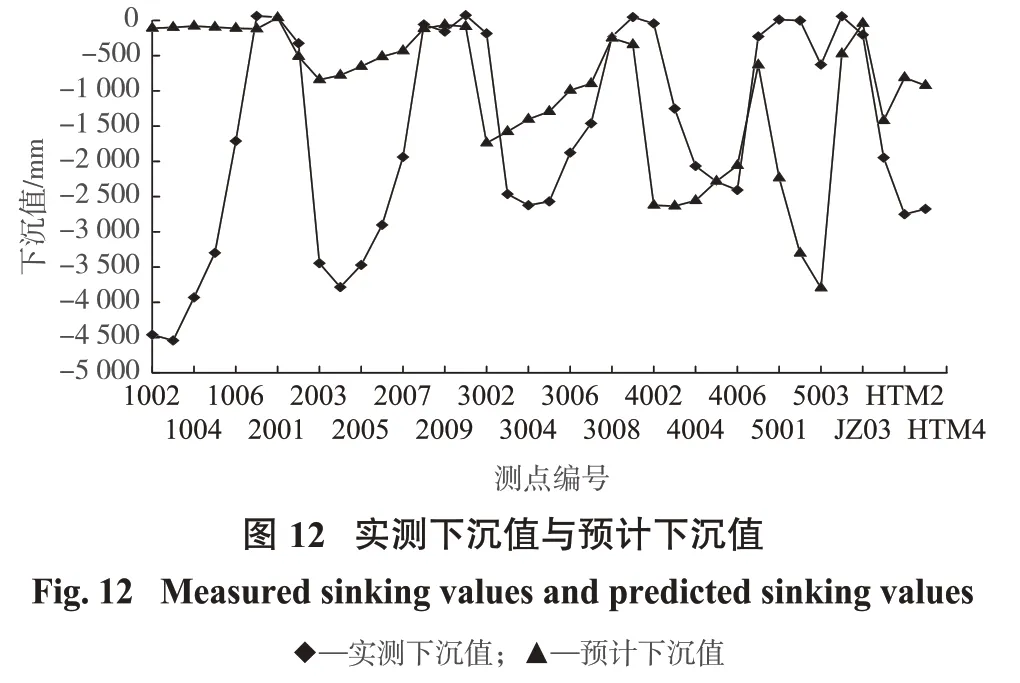
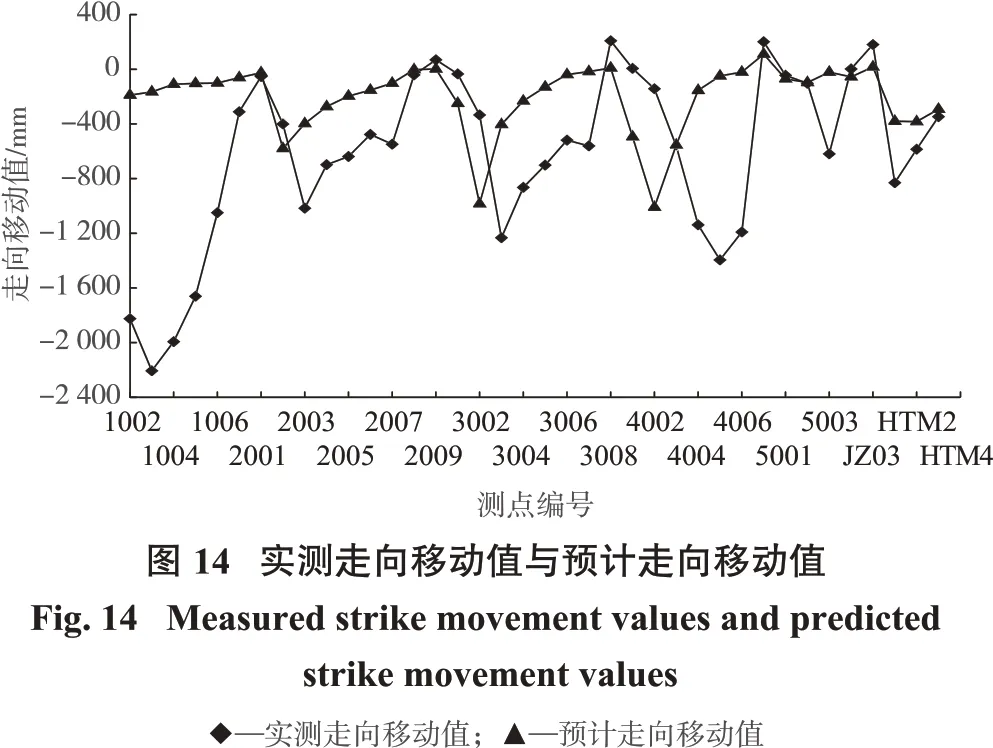
矿区在地表布设有若干观测点，并已获取到一定时间段内的经纬度和高程观测数据，通过坐标转换工具箱将原始数据转为系统内对应坐标，位于默认绘图范围内的观测点有38个。将观测点在统一坐标系内的坐标值输入系统进行批量查询，并输出系统预计值。预计值与实际观测值的对比结果如图12、图13、图14所示。

本研究预计系统可针对地表移动变形值的变化提供较好的趋势发展预计结果。图12 中，点1002～1006 间预计下沉值较小，下沉趋势呈现同步水平下沉，与实际观测值呈现的凹形下沉趋势差别较大，其他点位间的预计值与实际观测数据之间呈现出良好的凹形发展趋势。图13 中，预计倾向移动值的变化趋势与实际观测值相似，但移动方向相背，趋势表现不同步，表明在本例中对倾向移动值的预计没有意义，但是否对所有的矿区都不适用，需要进一步研究。图14 中，预计走向移动值与实际观测值间的发展趋势与图12 的下沉值相似，在点1002～1006 间预计值与实测值的凹形发展趋势相差较大，在点1007 之后的预计值与实测值整体表现出良好的凹形发展趋势，仅在个别点位出现偏差。

通过进一步分析可知：下沉值与走向移动值的预计结果较好地符合了实测值的发展趋势，符合发展趋势的点位占全部观测点的86.8%，而对倾向移动值的预计背离了实际，基本与实测值呈现相反的移动方向，无法提供有效的预计结果。在本例中所体现的数据误差来自几个方面，一是预计系统中地表曲面拟合产生的误差，地形越复杂误差越大，可能对水平移动值产生影响；二是采用的矿区参数不能完全反映实际开采情况，本例中工作面邻近区内已经存在有其他开采工作面，叠加效应将影响到实测值的变化，且并未排除，因此出现了实测下沉值大于预计下沉值的现象；三是受地质条件、数据采集精度等因素影响。

3 结 论

（1）将皮尔森Ⅲ型公式法与山区地表移动预计模型进行叠加计算，可实现对山区急倾斜煤层开采地表移动变形的近似预计。实现方法主要是通过Matlab语言对计算公式封装开发出可视化预计系统，系统将山区地表拟合生成曲面函数，为计算地表坡面任意点的倾斜方向角、倾角等参数提供了方便。另外，预计系统可以对最终生成的移动变形函数进行采样绘图，实现在预计范围内的二维、三维可视化分析，从而可以更加直观地展示预计结果和地表变形规律。

（2）通过结合实际矿区的开采条件和观测数据，确定了采区相关参数，利用本研究预计系统进行地表移动变形预计，得到了观测点的预计值，并将预计值与实测值进行了对比分析。结果表明：实测下沉值、走向水平移动值与预计值的整体发展趋势基本符合，仅个别点位存在误差，倾向水平移动值的预计效果较差，在本例中没有参考意义，可能受到系统地表曲面拟合精度、采区地质条件、数据采集误差等因素的影响，仍需要进一步验证分析并继续改进。通过分析可知：本研究开发的预计系统可以对山区急倾斜煤层开采引起的地表移动变形发展趋势进行近似预计，但由于受到误差影响，会出现偏离预计的现象，因此应尽可能保证各项开采沉陷预计参数精确取值。