基于压缩感知和随机像素置换的多图像联合加密方案
田强宝,谢 冬
(安徽师范大学计算机与信息学院,安徽 芜湖 241002)
0 引言
传统的信号获取与处理过程包括采样、压缩、传输、解压缩4个部分,其采样过程遵循奈奎斯特采样定理.这种方式采样数据量大,先采样后压缩,浪费了大量的传感元、时间和存储空间.压缩感知(Compressed Sensing,CS)理论是由D. Donoho、 E. Candes以及华裔科学家T. Tao等人提出[1-3].CS的优势在于在采样信号的同时,就对采样数据进行压缩处理.这种“少采样,巧计算”的原则,用后端处理器的计算优势减轻前端采样设备的负担,使得超带宽信号的处理更加有效.除了在信号处理领域以外,CS也被应用于图像加密[4],无线传感网络[5],遥感图像处理[6],图像采集设备的开发[7],光学成像系统设计[8],数字水印[9]等领域.
多图像加密作为一种新兴多媒体安全技术,在信息安全领域更是一个重要的内容.常用的图像加密技术包括置乱[10]、混淆[11]与扩散[12].但传统的图像加密方案并不能减少密文数据量,如采用数据加密标准(Data Encryption Standard, DES)或高级加密标准(Advanced Encryption Standard,AES)对像素点进行加密.而压缩感知加密实现了发送端采样、压缩和加密同时完成以及接收端解密、解压、重构同时完成;并且在此过程中能够保证图像传输的实时性和安全性.非常适合用于图像这种大数据量和高冗余度的信号通信中.目前国内外对压缩感知与图像加密相结合的研究也较多.吴小博等[13]等从图像的像素级与位级设计了联合加密技术,测试数据显示了其加密方案有效性.唐等提出了一种基于位平面和混沌映射的多图像加密算法[14].然而该算法每次只能加密4幅图像.2005年,HE等[15]提出了基于相位匹配技术的多图像加密和水印算法,实现了多图像隐藏加密,显著提高了数据传输的效率.
为提高多图像内容传输安全性,提出基于压缩感知理论与随机像素交换算法相结合的多图像联合加密方案,在降低密钥的空间大小同时提高加密系统安全性.本文中对算法进行了测试,证实了算法的有效性.
1 基础知识
1.1 压缩感知
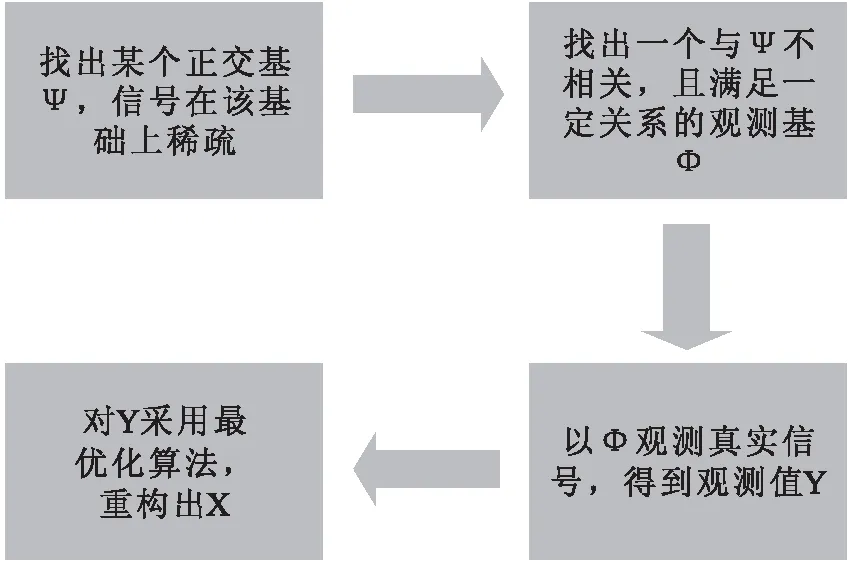
图1 压缩感知理论基本过程图Fig.1 Basic process of compressed sensing theory
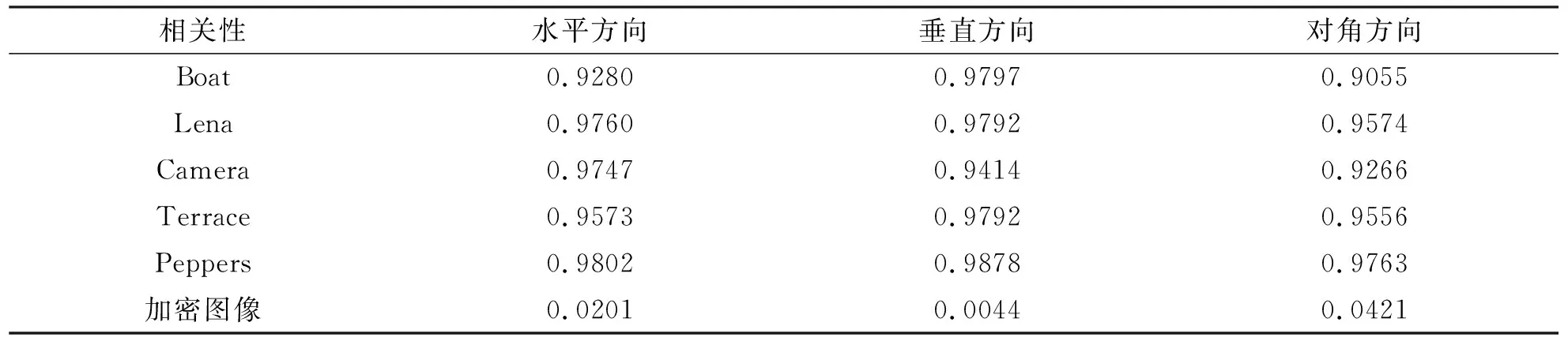
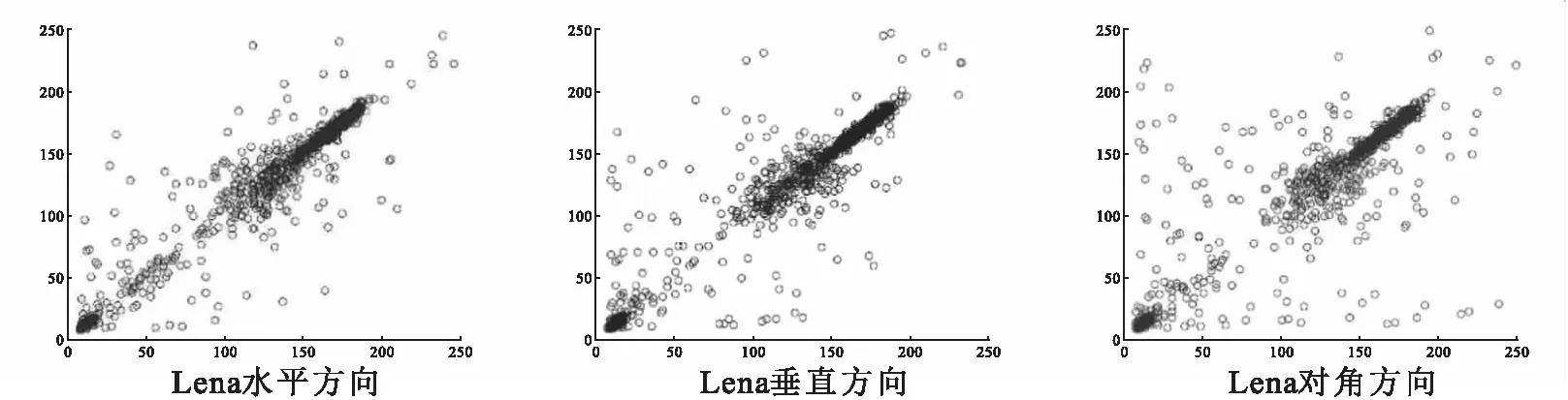
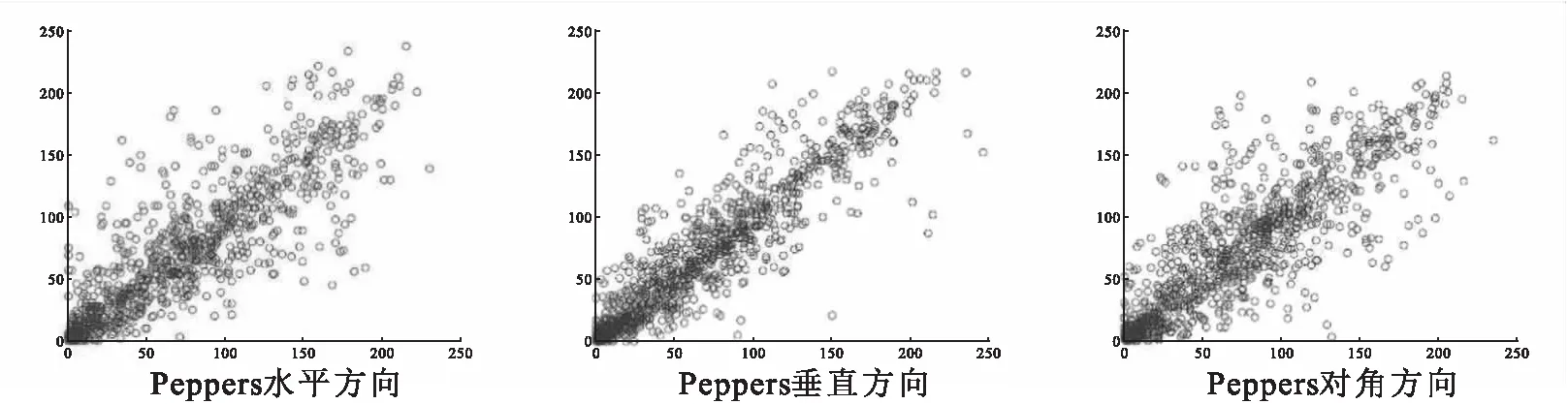
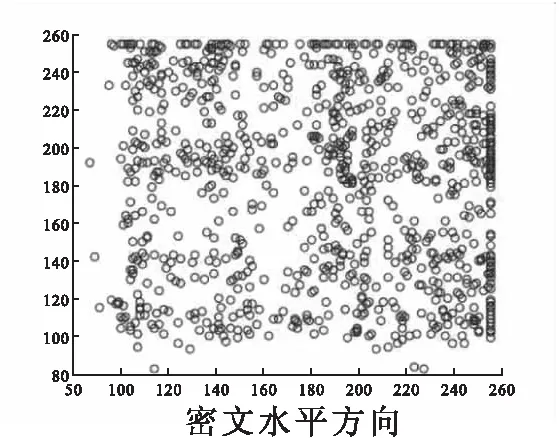
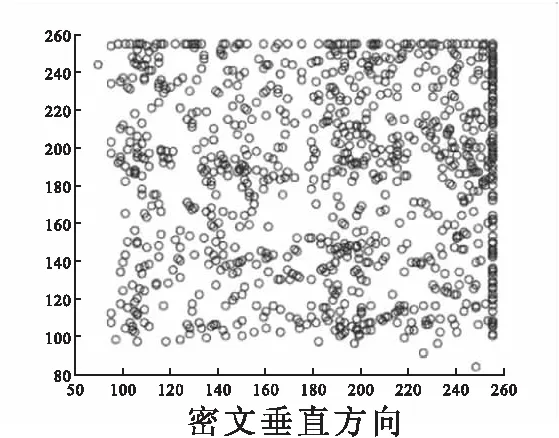
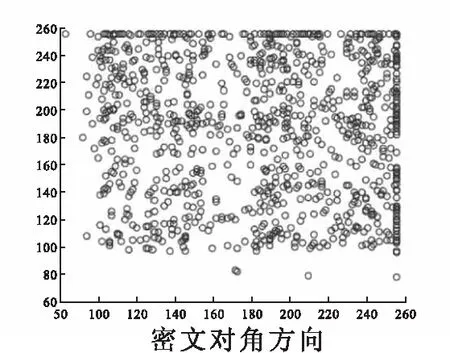
传统压缩技术从信号本身特性来寻找和消除数据冗余,这种压缩算法复杂消耗较大.而压缩感知直接感知压缩后的信息,信号采集和压缩同时完成,只要一个信号在某个变换域中是可压缩的或稀疏的,就可以利用测量矩阵将高维信号转换为低维空间,进而信号重构问题也就转换为一个优化问题求解.其理论依据如下[16]: 1)假设有一个长度为N的信号X在某个正交基Ψ上是K稀疏的(即含有K个非零值);2)找到一个与Ψ不相关的观测基Φ;3)用观测基Φ观测原信号得到M维的观测向量Y,其中K 随机像素交换[17](random pixel exchanging, RPE)是对相同维度图像中像素进行交换的方法.假设I1与I2分别是两个维度相同的矩阵,矩阵大小为M×N,R是一个与I1、I2维度相同的随机矩阵(本文取同维的测量矩阵),值范围限于[0,1],‘’表示交换两个矩阵位置的值,A1'和A2'表示完成随机像素交换后的矩阵.随机像素置换算法数学公式如下: (1) 1≤m≤M, 1≤n≤N,其中M,N是随机矩阵R的维度,‘round’表示四舍五入函数.随机矩阵R的平均值计算如下: (2) 图2 随机矩阵置换过程图Fig.2 Random permutation process 本文采用OMP[18]算法(正交匹配追踪算法)来对密文图像进行解密重构.OMP算法沿用了MP算法中的原子选择准则,即通过求余量r与感知矩阵Φ中原子之间内积的绝对值来选择最佳原子组合,不同的是OMP在分解的每一步对所选择的全部原子进行正交化处理,这使得在精度要求相同的情况下,OMP算法的收敛速度更快. 对于n幅明文图像,方案的加密过程首先利用Logistic混沌序列构造测量矩阵进行压缩,然后对压缩后每两幅图像之间利用RPE算法进行多轮交换置乱,以此来提高密文的安全性(如图3所示).对于解密过程,首先将密文图像分割成n部分,按照RPE逆顺序对n幅分割的图像进行随机像素逆交换得到压缩图像,再利用OMP重构算法依次进行解密(如图4所示). 图3 加密过程Fig.3 Encryption process图4 解密过程Fig.4 Decryption process 2.1.1 加密过程 Logistic混沌映射为: Xn+1=μXn(1-Xn),Xn∈(0,1) (3) 图5 图像间像素随机置换Fig.5 Random replacement of pixels between images 其中μ∈[3.57,4].假设测量矩阵维度为M×N,首先利用初值为X1的Logistic混沌映射产生长度为M×N×q+1的序列,每隔q个元素取一个元素依次填充到测量矩阵中[20].其次将矩阵随机像素交换与测量矩阵捆绑.具体加密过程如下: ①利用密钥X1,X2,…, Xn构造n个大小为M×N的测量矩阵Φ1,Φ2,…,Φn.分别使用Φ1,Φ2,…,Φn测量A,B,…,N,测量结果为A1,B1,…,N1.②按照图5所示的顺序对测量后的图像进行像素交换.由于随机矩阵R1,R2,…,Rn的元素值范围都固定在[0,1],测量矩阵的元素值范围为[0,λ],且随机矩阵和测量矩阵的维度相同,因此将随机矩阵和测量矩阵捆绑.设定Rn=Φn/λ.如图5所示图像A1与图像B1交换使用随机矩阵R1,图像B1与图像C1交换使用随机矩阵R2,以此类推. 2.1.2 解密过程 解密的执行过程如下:①随机像素逆置换.按照RPE的逆交换顺序进行像素交换,得到压缩后的图像.②OMP重构算法对压缩图像进行解密. 为验证所提出加密方案的正确性,实验首先用256*256灰度图片Lena和Building作为第一组联合加密的明文图像.Logistic混沌映射的初值要求范围在(0,1),本组实验分别取X1=0.11,X2=0.23,μ=3.792,q=2,M=192(将图像加密压缩为原图的3/4).加密和解密结果如图6所示. 为扩大联合加密的样本容量,并同时分析本文所提出的算法对奇数张和偶数张图片是否都适用.本组实验使用256*256的灰度图像Lena、Peppers和Bear作为实验样本.实验测量矩阵初值分别为X1=0.11、X2=0.23和X3=0.89.混沌序列的参数为μ=3.798,q=2,测量次数M=192.加解密效果如图7所示. a)明文Building; b)明文Lena; c)密文图像; d)解密的Building; e)解密的Lena图6 加解密效果示意图(Ι)Fig.6 Effect demonstration of encryption and decryption(Ι) a)明文Building; b)明文Lena; c)明文Bear;d)密文图像; e)解密的Building; f)解密的Lena; g)解密的Bear图7 加解密效果示意图 (Ⅱ)Fig.7 Effect demonstration of encryption and decryption(Ⅱ) 为分析方案的容错率,本组实验将采用4副256*256的灰度图像Lena, Couple, Boat以及Plane作为实验样本.实验测量矩阵的4个初值分别取X1=0.11,X2=0.23,X3=0.1,X4=0.3.混沌序列的参数为μ=3.99,q=2,测量次数M=192.加密解密效果如图8所示. 为验证奇数张图片以及融合非标准测试图片下方案是否可靠,本组实验采用256*256的灰度图像Boat,Lena,Camera,Terrace以及Peppers作为实验样本.测量矩阵的初值分别取X1=0.11,X2=0.23,X3=0.1,X4=0.3,X5=0.34,混沌序列参数为μ=3.1779,q=2,测量次数M=192.加密解密效果如图9所示. 以上4组实验表明本文方案提出的多图像加密算法可以针对任意多副的明文图像进行联合加密,且解密端重构的图像效果较好. a)明文 Lena; b)明文 Building; c)明文 Bear; d)明文 Lady ; e)密文图像; f)解密的Lena; g)解密的Building; h)解密的Bear; i)解密的Lady图8 加密解密效果示意图(Ⅲ) Fig.8 Effect demonstration of encryption and decryption(Ⅲ)a)明文Building; b)明文 Farmland; c)明文 Plane; d)明文Movie; e)明文 Ship; f)密文; g)解密的Building; h)解密的Farmland; i)解密的Plane; j)解密的Movie; k)解密的Ship图9 加密解密效果示意图(Ⅳ)Fig.9 Effect demonstration of encryption and decryption(Ⅳ) 表1 2幅图像联合加密不同方向的相关系数Tab.1 Two images jointly encrypt correlation coefficients in different directions 表2 3幅图像联合加密不同方向的相关系数Tab.2 Three images jointly encrypt correlation coefficients in different directions 表3 4幅图像联合加密不同方向的相关系数Tab.3 Four images jointly encrypt correlation coefficients in different directions 表4 5幅图像联合加密不同方向的相关系数Tab.4 Five images jointly encrypt correlation coefficients in different directions 表1至表4分别介绍了2副、3副、4副以及5副图像联合加密后所得出的明文图像和密文图像不同方向的相关性系数.通过对比可以发现各个试验中明文图像的不同方向相关性系数接近于1而密文图像不同方向的相关性系数均小于0.1,此结果说明明文图像像素点之间相关性较高,而密文图像像素点之间相关性较小.图9 展示了5副图像联合加密的明文图像以及密文图像各个方向上的相关性.以上相关性分析可以得出本文所提出的算法具有较好的明文图像置乱效果,算法安全性较高. 图10 5幅图像联合加密明文图像以及密文图像各个方向上的相关性Fig.10 Five images combined with encrypted plaintext images and correlations in all directions of ciphertext images 本文基于压缩感知与随机像素交换技术,提出一种可以实现多幅图像同时加密传输的方案.将Logistic映射产生的测量矩阵与随机像素交换矩阵相捆绑,提高了整个加密系统的安全性.实验结果表明方案具有正确性,抗攻击性较强特点.1.2 随机像素交换算法


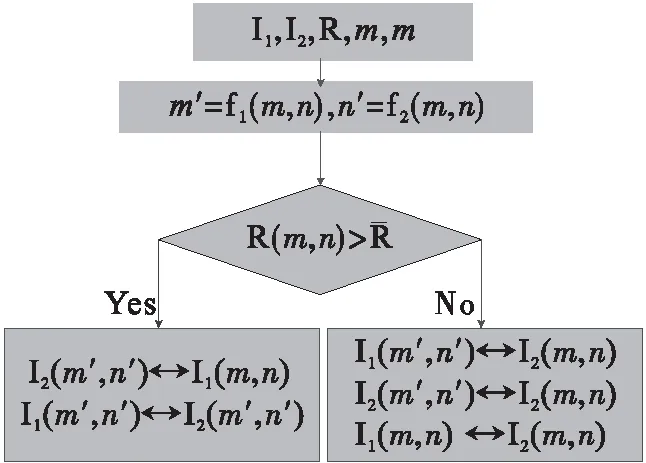
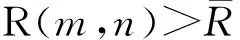
1.3 图像解密算法
2 基于压缩感知和随机像素置换的多图像联合加密方案
2.1 方案描述


3 实验分析
3.1 正确性


3.2 加密解密结果相关性分析

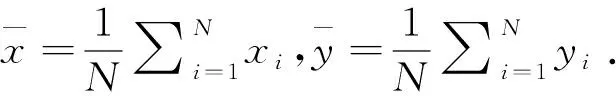





4 结论

