均值-方差联合模糊不确定情况下的委托代理问题

张 琪，陈晓燕，朱元国

(南京理工大学理学院，江苏 南京 210094)

近年来，隐藏行为的研究文献主要是在奈特不确定下，即产出的分布具有模糊不确定的框架下对委托代理的最优契约问题进行研究. 2002年Chen 和Epstein[1]利用倒向随机微分方程和等价概率测度，在连续时间模型下考虑了产出存在均值模糊的情况，指出委托人和代理人在模糊厌恶的态度下会选择相同的最悲观的概率测度或分布.2008年Epstein和Schneider[2]在离散时间模型下考虑了产出方差的模糊情况，通过假定工资是产出的线性函数，给出不同代理人在模糊厌恶下也会选择相同的最悲观的概率测度或分布. 2010年Weinschenk[3]在离散时间下同样假定工资为产出的线性函数，考虑委托人和代理人具有相同的模糊厌恶态度.结论是，若产出只有均值(或方差)模糊，那么委托人和代理人会选择相同的最悲观的概率测度或分布.但是，当产出的均值和方差联合模糊时，该文献发现委托人和代理人可能会选择不同的概率测度或分布.2015年Miao和Rivera[4]考虑了连续时间情况下产出具有均值模糊的委托代理问题，发现最优契约是激励与模糊分担之间的一种权衡. 2018年Sung[5]在连续时间模型下，在均值方差联合模糊不确定的基础上，考虑了对产出的均值的控制.该文献给出了最优工资方案是产出和产出的可验证方差的线性函数，并证明了委托人和代理人在同样模糊厌恶的情况下会选择相同先验的概率测度或分布. 在该文献的基础上，2018年ChenX[6]通过假设工资为产出和产出的可验证方差的线性函数，论证了委托人和代理人在模糊厌恶态度下会选择相同的均值和方差所对应产出的先验概率分布，并证明了绩效工资敏感度贝塔是随预测的产出波动率递减的，这与1999年Aggarwal和Samwick[7]的经验数据一致.

本文主要是在均值方差联合模糊不确定的基础上，考虑对均值和方差均有控制，给出了契约形式.结果表明，考虑第一最优契约问题时，委托人与代理人关于最糟糕的先验选择是能达成一致的，且模糊与控制并不会影响产出的风险分担和模糊补偿.

1 预备知识

1.1 模型

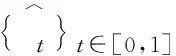
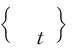
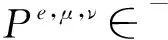
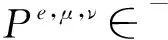
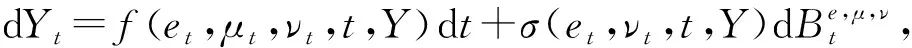
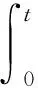
在分析合约问题之前，定义如下的Hamiltonians式子.对于((e,μ,ν),β,θ,t,Y)∈U×Dt(Y)×R×R×[0,1]×Ω,HA(μ,ν;e,β,θ;t,Y)=-c(e,t,Y)+φA(μ,ν;e,β,θ;t,Y),

且对于(e,β,θ,(μP,νP),p,t,Y)∈U×R×R×Dt(Y)×R×[0,1]×Ω,

HP(μP,νP;e,β,θ;p,t,Y)= -c(e,t,Y)+φP(μP,νP;e,β,θ;p,t,Y)+

本文所要解决的最优问题的一般形式为如下问题：

(1)

s.t.dYt=f(u,v,t,Y)dt+σ(u,v,t,Y)dBu,v,

其中，g,q,h,f,σ为实值函数，使得g,q,h,f:U×D×[0,1]×Ω→R,σ:U×D×[0,1]×Ω→R+

Ho表示如下的Hamiltonian式子：对于所有的(ut,vt,p,t,Y)∈Ut(Y)×Dt(Y)×R×[0,1]×Ω,

(2)

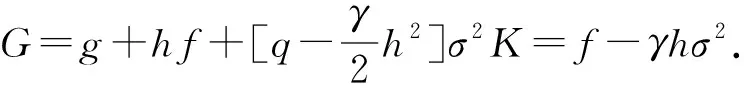
1.2 假设条件

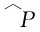
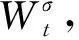
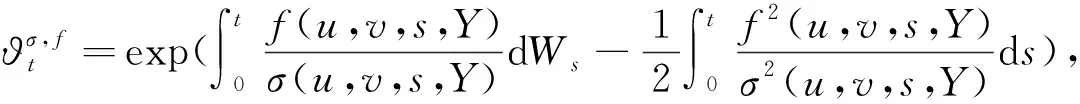
注：在本文中，Pu,v=Pe,v=Pe,μ,ν.

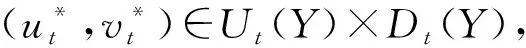
假设4假设f,σ,c分别关于(e,μ,ν),(e,ν),e是连续可微的；f,c,σ关于e严格递增，σ关于ν严格递增.

注：Ee,μ,ν表示测度Pe,μ,ν(Pe,v)下的期望算子，记为Ee,v；Ee,ν表示测度Pe,ν下的期望算子，记为Ee,ν.

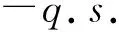
2 容许合约的表示形式

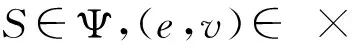
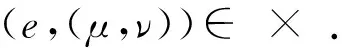
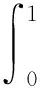
(3)

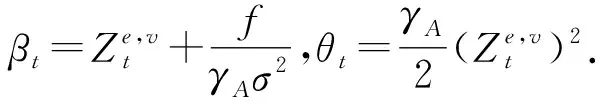
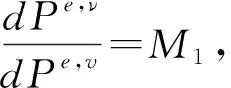
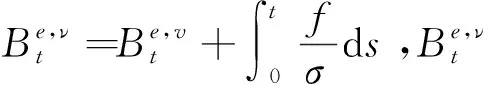
因此，由测度变换可知，代理人的期望效用等价于

s.t.dYt=σ(et,νt,t,Y)dWt,

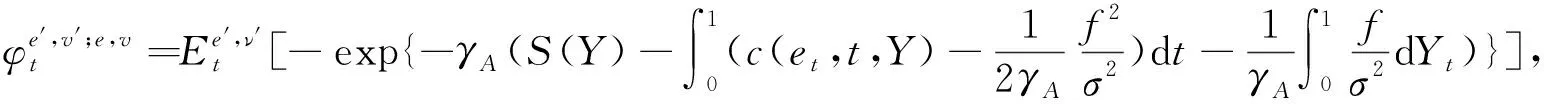
(4)

(6)

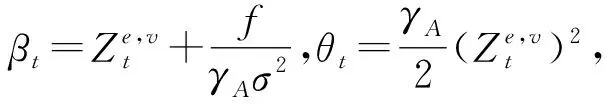
3 第一最优契约问题

问题1(第一最优)委托人与代理人通过解决下面的问题来签订一份合约.

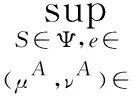
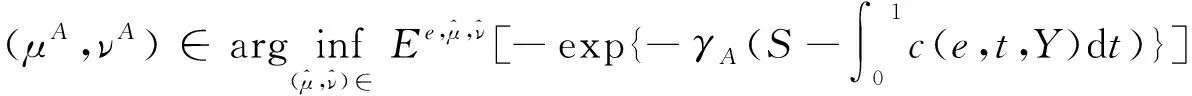
约束(ⅱ)使得代理人选择最糟糕的模糊参数过程.约束(ⅲ)可以保证代理人的参与，即达到他的保守效用.

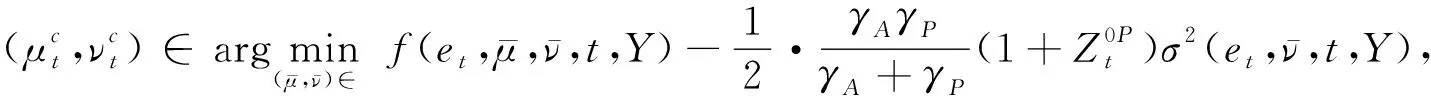
(8)

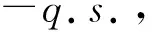
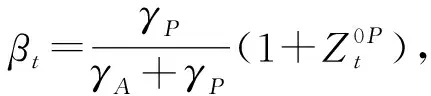
证明(1)求出关于问题1的Hamiltonian式子

类似于文献[5]定理3的证明，问题1的后两个约束条件可以被替换为如下的约束条件：

(9)

因此，委托人的问题可以被等价地表示为如下形式：

(2) 求出最优化问题所对应的一阶条件

由于φA和φP都是连续可微的且Dt(Y)满足KKT(Karush-Kuhn-Tuckler)约束条件，因此,关于(μ,ν)的一阶条件是委托人和代理人的最优化问题的必要条件，且运用包络定理得到关于(e,β,θ)的一阶条件，如下：

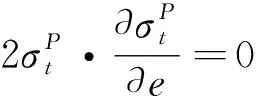
(10)

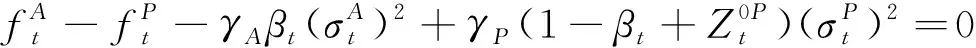
(11)

(12)

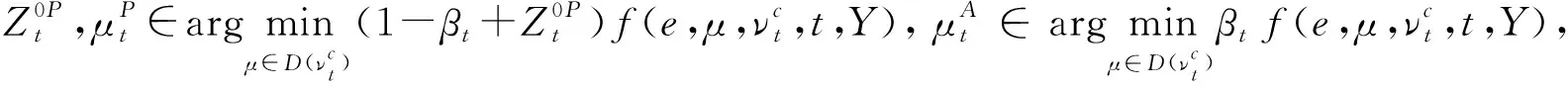
(3)具体分析，并给出最优解

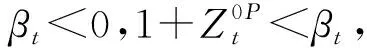
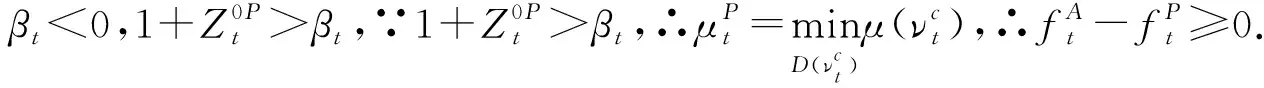
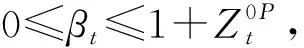
(13)

(14)

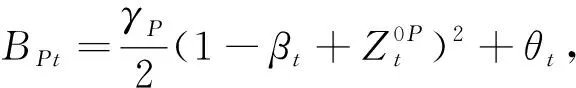
(15)

(16)

那么，委托人和代理人问题关于(μ,ν)的一阶条件如下：存在拉格朗日乘子λPt,λAt≥0,使得

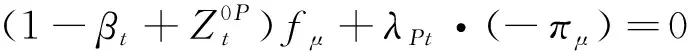
(17)

(18)

λPtπ=0,π≥0

(19)

βtfμ+λAt(-πμ)=0

(20)

(21)

λAtπ=0,π≥0

(22)

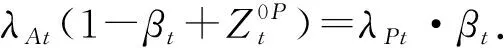
根据θt=0且βt满足式(13)，最糟糕的先验选择最小化φA和φP等价于解决式(8).由此可以得到定理2所给出的最优契约的形式.命题得证.

4 结论

通过考虑产出的均值和方差具有模糊和控制时，定理1给出了最优契约形式.结果表明，在定理1所给出的最优契约形式下，考虑第一最优契约问题时，委托人与代理人关于最糟糕的先验选择是能达成一致的，且模糊与控制并不会影响风险分担和模糊补偿.因此，在考虑第一最优契约问题时，不需要考虑对产出均值和方差的模糊及控制，只需要考虑产出的风险不确定性，这大大简化了第一最优契约的模型.