粗糙势能对Frenkel-Kontorova晶格热传导性能的影响

周步云， 艾保全

(华南师范大学物理与电信工程学院， 广州510006)

近20年来，低维热传导机理的研究引起了广泛关注，低维热传导也表现出与宏观材料不同的特性，最大区别是在低维系统中傅里叶定律是否有效. 一般来说，一维模型可以分为3类[1-2]：(1)可积分系统,例如关于谐波链的研究[3]表明在这一类系统中不存在温度梯度，并且热导率是发散的；(2)不可积分系统,Frenkel-Kontorova模型[4-5]和Lorentz气体模型[6]都是经典的例子，傅立叶定律在此类系统中有效；(3)特殊的不可积分系统，例如Fermi-Pasta-Ulam链[7-8]和双原子Toda链[9]等，该链中存在温度梯度，但热导率随热力学极限发散. 对低维材料的理论研究不仅增加了对热传导机理的认识，而且为设计各种热装置开辟了道路. 一些研究提出了有趣且实用的热学器件，例如整流器[10-13]、热二极管[14]、晶体管[15]、热逻辑门[16]、隔热斗篷[17-18]、热记忆[19]、热泵[20-21]、热限流器[22]和恒热源[22]等，这些研究关注非线性响应机制. 在非线性响应状态下，负微分热阻(NDTR)是一种违反直觉的、特殊的物理现象，其热流随温度差的增加而减小，这可能成为某些热器件的物理机制，近年来引起了广泛关注.

目前对Frenkel-Kontorova模型的研究集中于标准Frenkel-Kontorova晶格模型[5,23]、由2段Frenkel-Kontorova晶格组成的模型[10,14]和由3段Frenkel-Kontorova晶格组成的模型[24]，但是对原子所处的粗糙势能对热传导影响的研究尚少.

1 研究方法

具有粗糙周期性的FK链哈密顿量可描述为：

其中，pi表示第i个原子的瞬时动量；xi表示第i个原子偏离平衡位置的瞬时位移.V(xi+1-xi)表示最近相邻原子的交互势能：

其中，K0为FK链的弹簧常数.U(xi)表示粗糙周期势能：

其中，V0为势能的高度；r为粗糙势能的高度；ω为粗糙部分势能的频率. 如图1所示，当选择r=0时，则标准的FK链势能曲线光滑；当r≠0时，势能变得粗糙并带有凹槽. 增大ω会使总势能的粗糙度增大，因此可以通过改变r或ω来改变粗糙势.

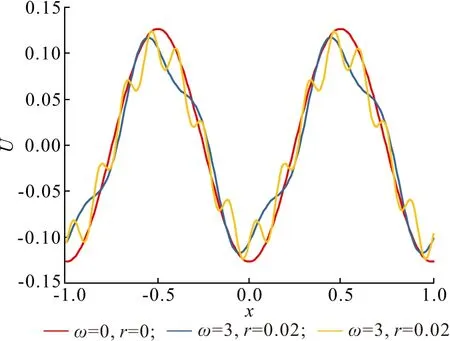
图1 V0 = 5时粗糙势能U(x)随x的变化

Figure1 The rough potentialU(x) as the function of displacementxin the case ofV0= 5

在数值模拟中，FK链的两端分别固定在T+和T-温度下，以实现稳定的热流. 链两端的温度由Langevin heat baths提供. 为了固定链，x0和xN+1都作固定边界条件，取值为零.

其他原子的运动方程为：

其中，m是原子质量.γi和ξi的定义如下:

γi=γ(ξ+δ1,i+ξ-δi,N)，

ξi=(ξ+δ1,i+ξ-δi,N)，

其中，γ表示摩擦系数；δ表示狄拉克δ函数；ξ表示高斯白噪声. 其耗散关系为：

〈ξ(t)ξ(t′)〉=2γkBTδtt′，

〈ξ(t)〉=0，

其中，kB是玻耳兹曼常数；〈…〉表示一段时间内的总体平均值.

为便于计算，将玻尔兹曼常数和原子质量设为1，即kB=γ=1. 计算局部热流的方程为：

计算局部温度的方程为：

经过长时间的模拟，系统达到稳定状态，局部热流ji与原子位置i无关，因此总热流可以通过J=Nj计算.

通过声子态密度(PDOS)解释热传递性质是一种有效方法. PDOS是在给定频率间隔内变化的动能分布. 通过计算速度自相关函数的傅立叶变换，PDOS可描述为[25]：

其中，ω是声子的频率；vj表示第j个原子的速度矢量，〈…〉表示所有原子和所有时间的平均值.

2 结果与讨论

2.1 粗糙势能对负微分热阻的影响

2.1.1 负微分热阻与粗糙高度的关系 在ω=3、T-=0.001、V0=5、K0=0.5、N=32条件下，不同r=0～0.10时，绘制总热流与T+的函数图像(图2).

图2 不同r取值时总热流J随T+的变化

注:T-=0.001，ω=3，V0=5，K0=0.5，N=32.

在一定温度范围，如果出现温差较大而产生的总热流较小，则说明出现NDTR. 当r<0.05时，NDTR 出现；当r>0.05时，NDTR消失. 与r=0的情况相比，当r<0.05时，增加r会使NDTR的范围变小. 图2还说明存在一个临界温度Tc，当温度T+>Tc时J随r的增加而增大. 这是因为高温使颗粒易于克服势能，原子更加趋向远离x=0处的势能凹槽中，势能凹槽的深度随r的增加而增大，增加r可使槽中的原子比标准FK链中的原子获得更多的动能，故增加r时热流J增大.

当r=0.01和T-=0.001时，NDTR出现规模效应(图3). NDTR的范围变得更小，最终随着系统大小N的增大而消失. 这是因为NDTR可能是某种边界机制的结果，例如声子边界散射或边界热阻，当N增加时，边界机制的影响减小. 在T+=0.070、0.154、T-=0.001情况下，得到PDOS图(图4). 与T+=0.154的情况相比，当T+=0.070时，PDOS在低频下较高，因此，热流在T+=0.070时比在T+=0.154情况下的大，NDTR出现. 当r=0.05时，在T+=0.154情况下，PDOS的低频部分大于T+=0.070的情况，因此NDTR消失.

图3 不同系统大小(N)条件下总热流J 随T+的变化

Figure 3 The change of total heat fluxJas a function ofT+for different system sizes (N).

注:T-=0.001，ω=3，V0=5，K0=0.5.

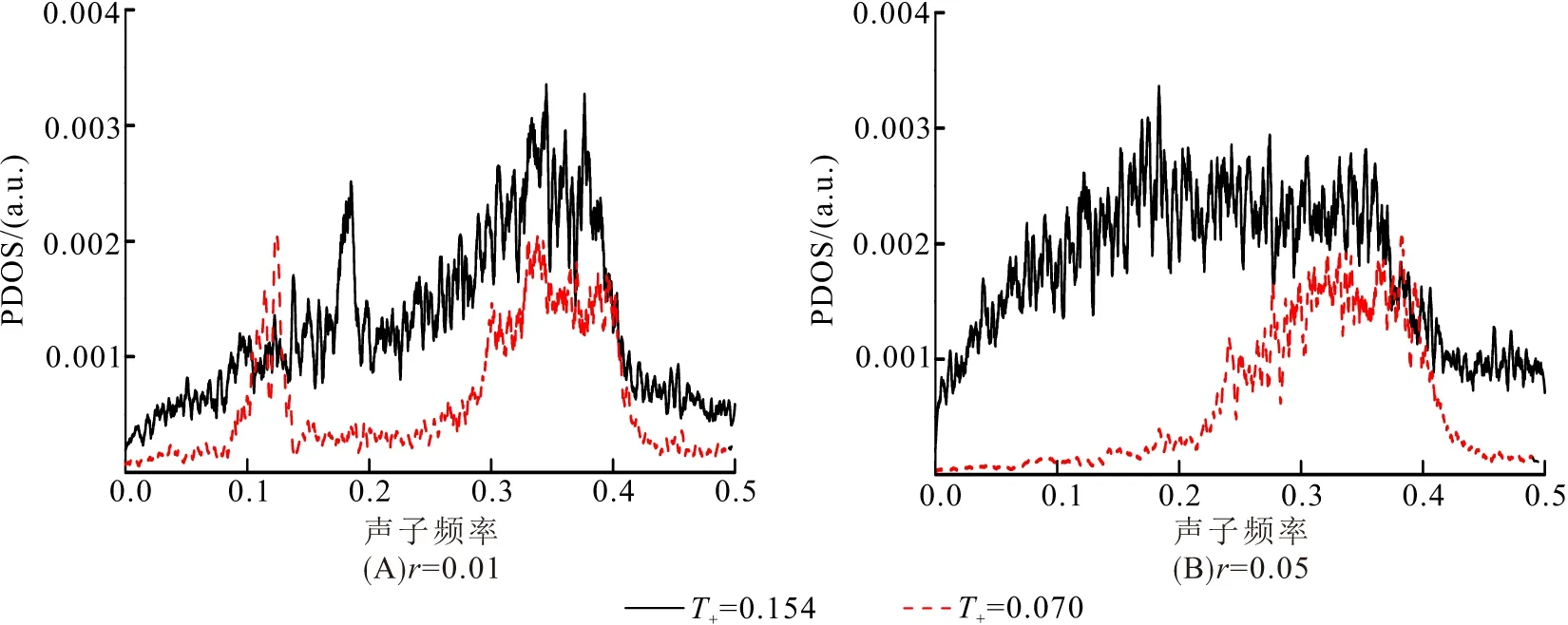
图4 PDOS与频率的函数图像

2.1.2 负微分热阻与粗糙频率的关系 由总热流J与T+的关系(图5)可知，当固定T-=0.001，而对ω取不同值时，NDTR出现，但随着ω的增加，NDTR逐渐消失. 随T+增大，ω对热流的影响减小，最后热流趋向相同，这是因为温度升高原子运动剧烈，粗糙势能对原子的作用力比热源的作用力小，因此改变ω热流的变化不大. 当T+=0.154时声子态密度的低频部分比T+=0.070时的大，NDTR消失(图5).

图5 不同ω与T+时的总热流和PDOS图像

2.2 粗糙势能对热导率的影响

对于不同的ω，热导率κ与粗糙势能高度r的关系如图6所示.r对热导率κ的影响随粗糙度频率ω的不同而变化. 当ω=1时，κ与r单调增加，这是由于总势能高度r降低所致. 当ω从1开始增加时，κ会增加，然后随着r的增加而减少，即存在一个峰值κm，κm是ω的函数.

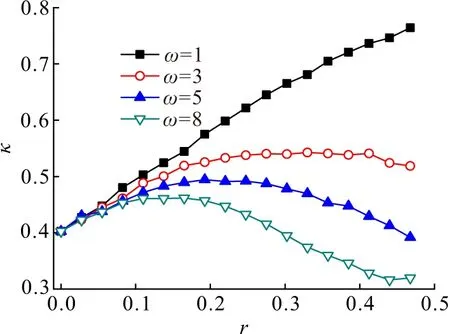
图6 热导率κ与r的关系

当ω=1时，粗糙势可以写成

其中，

φ=arctan(r-1)，

它表明增加r会降低势能的最大值，因此热流增大. 由图1可知，当ω>1时，粗糙势能会引起沟槽. 与r=0的情况相比，当r≠0时处在凹槽底部的原子将获得较少的势能，并且随着r的增加，凹槽越深，获得的势能越小，势能越小原子获得的动能越大. 当r较小时，原子可以穿过x=0附近的凹槽到达远离x=0的凹槽，增加r可使处在槽中的原子比处在标准势能的原子获得更多的动能，在这种情况下，增加r意味着原子更容易传导热流. 当r增加时，原子被困在接近x=0的凹槽中，这使得热流变小.

由图7可知，κ随ω的增加而单调减少，并且设置不同的r可以控制κ的下降速度. 这是因为随着ω的增大，势能作用在原子上的力增大，导致原子运动的速度和范围变小. 因此，热流更难以从高温区域传递到低温区域，热导率减小. 由系统尺寸对热导率κ的影响(图8)可知，当系统大小N=64、128时，随r的增加，热导率κ先增大后减小，也具有最大值.

图7 热导率κ与ω的关系

图8 热导率κ与r的关系

3 结论

研究了Frenkel-Kontorova晶格处于粗糙势能下的热传导性能. 结果表明：当粗糙势能的高度、粗糙度的频率增加时，NDTR的范围变小，最终消失. 研究了热导率与粗糙势能高度和频率之间的关系，结果表明：在不同频率ω下，存在一个粗糙高度r最优值，热导率κ在该处取最大值. 随着系统尺寸的增加，粗糙势能仍可以对热导率起作用. 粗糙势能的频率增大可以使热导率单调降低. 粗糙势能的高度或频率增大将缩小NDTR的范围，这可能是导致在实际材料中几乎找不到NDTR的原因，因为在现实中建立标准势能场是一项较难的操作. 本文提出了一种可能的方法，即通过改变粗糙度FK势的高度和频率来控制低维晶格中的热导率.