多元线性模型在滨城区农田水利规划中应用
刘 帅
(滨州市滨城区水利局,山东 滨州 256600)
随着水资源短缺的问题日益严峻,水资源成为制约科技发展,社会进步的重要因素之一。合理利用水资源,加强农田水利建设规划,是水利部门的重要任务。
1 多元线性回归模型
1.1 多元线性回归模型的形式
由于在实际经济问题中,一个变量往往受到多个原因变量的影响,所以,在线性回归模型中的解释变量有多个,这样的模型被称为多元线性回归模型。多元线性回归模型参数估计的原理与一元线性回归模型相同,只是计算更为复杂。以多元线性回归模型的一般形式——K元线性回归模型进行分析,其模型结构如下:

式中:Y是被解释变量(因变量、相依变量、内生变量);x是解释变量(自变量、独立变量、外生变量),是随机误差项;i,i=1,…,k是回归参数。线性回归模型的意义在于把Y分成两部分:确定性部分和非确定性部分。
1.2 滨城区农田改造的分析
滨城区现存在Ⅰ类耕地0.27万hm2、Ⅱ类耕地0.50万hm2和宜垦荒地0.10万hm2,Ⅰ类耕地比Ⅱ类耕地条件好,适宜农作物种植。此地区主要农作物为小麦,靠7 000万m3地表水和30万m3地下水进行灌溉,小麦扬花时期恰逢枯水季节,可提供700万m3水资源。为进一步合理利用水资源,可采取两种措施:1)农田改造,可将Ⅱ类耕地部分改造成Ⅰ类耕地,每亩投资18元。对荒地进行开垦,改造为Ⅰ类耕地每亩投资105元,改造为Ⅱ类耕地每亩投资80元。2)修建水库,丰水期蓄水,小麦扬花期可增加750万m3水资源,建设水库投资500万元。规划期内计划总投资额度为950万元,规划年该地区对小麦的需求量及国家征购指标共计2.5万t,超出部分每吨净产值增加110元。各条件下灌溉定额及净收益见表1。
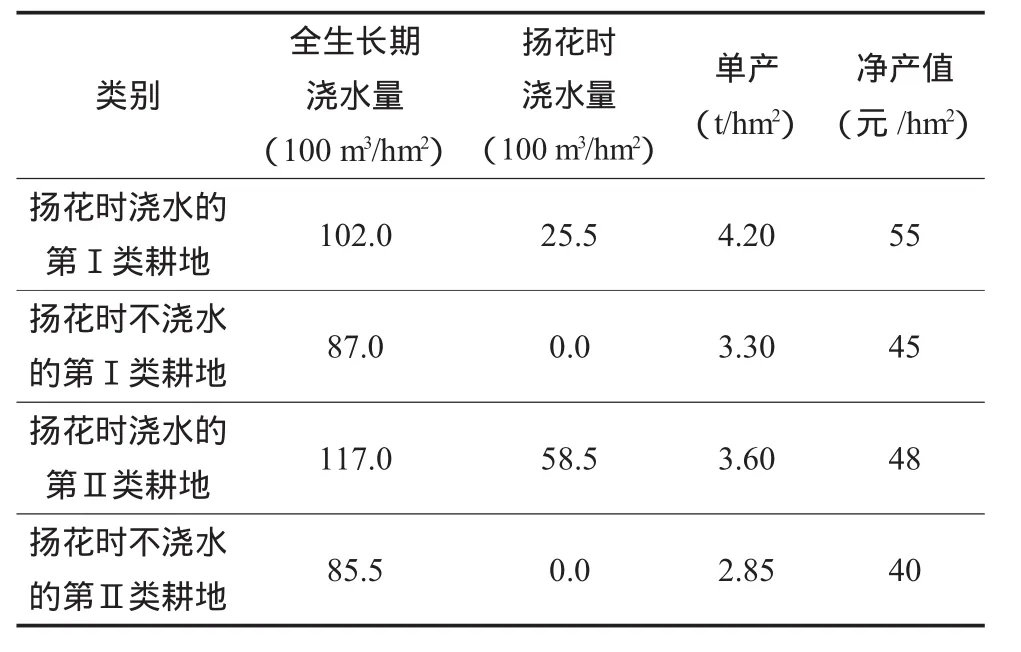
表1规划年各种条件下的灌溉定额及净收益
2 农田水利规划模型建立
选取合理的经济效益评价指标体系,建立简单规划模型。结合各类耕地需水量、单产及净产值数值,在供水量、投资额、小麦需求及征购量、土地面积的限制条件下,求出在充分利用水资源条件下的经济效益最优值。经计算,随规划期的增加,达到最大经济效益时的耕地水利建设模式基本保持不变,Ⅰ类耕地扬花期浇水面积为0.18万hm2,Ⅱ类耕地全部改造为Ⅰ类耕地,荒地开垦为Ⅰ类耕地面积为0.11万hm2,荒地不开垦为Ⅱ类耕地,不修建水库的方案下,可达最优经济效益。但长期规划情况下,建设水库才可达最优经济效益。之后结合粮食需求量、GDP增长、科技水平的进步等实际情况,建立优化模型,求出最优经济效益。
3 模型计算过程
设置 x1、x2、x3、x4、x5五个自变量,由题意可知,Ⅰ类耕地有0.23万hm2,Ⅱ类耕地有0.57万hm2,此外尚有宜垦荒地0.30万hm2,则:各类耕地面积为:

土地面积限制条件:结合实际情况可知,各类土地面积需不小于零,则有xi(i=1,2,3,4,5)≥0。
改造的耕地面积需不大于原有耕地总面积,则有:
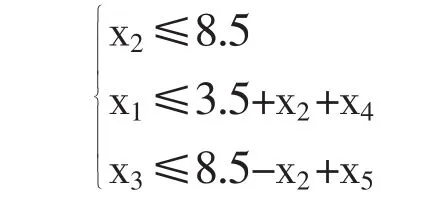
规划年收入:

目标函数:

运用lingo 11.0编程求解,规划期为1年时,各变量随规划期时间变化情况见表2。
由表2可知,从第5年开始将Ⅱ类耕地全部改造为Ⅰ类耕地,荒地改造为Ⅰ类耕地的面积为0.11万hm2,Ⅰ类耕地扬花时期浇水面积为0.18万hm2,不修建水库的方案下,可充分利用水资源,发挥最大的经济效益,此时获得最大利润。
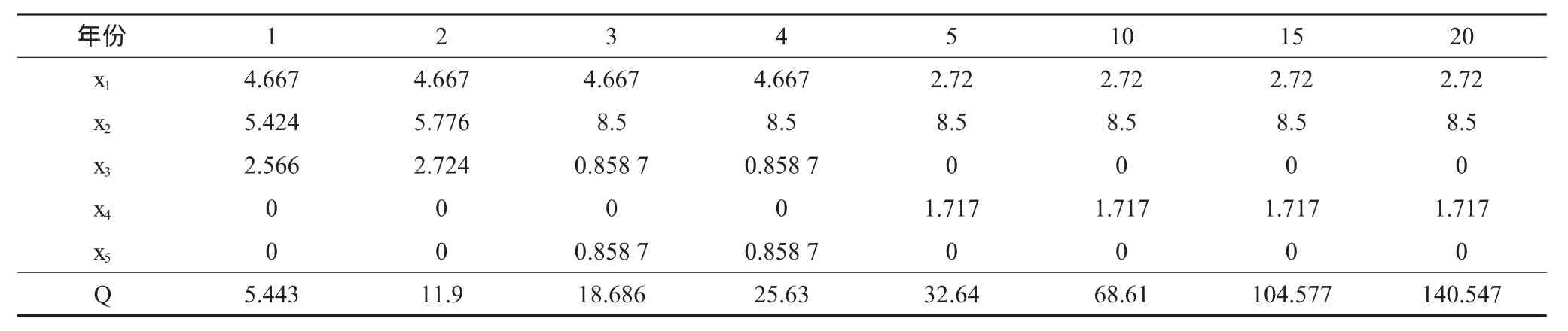
表2各变量随规划期时间变化情况表
4 结论
根据提供的耕地条件、需水量、小麦产量、投资额为限制条件,建立模型,运用lingo 11.0求解得:规划期为短期时,将Ⅰ类耕地扬花期浇水面积为0.18万hm2,Ⅱ类耕地全部改造为Ⅰ类耕地,荒地开垦为Ⅰ类耕地面积为0.11万hm2,荒地不开垦为Ⅱ类耕地,不修建水库的方案下,可达最优经济效益;规划期为长期时,将Ⅱ类耕地全部改造为Ⅰ类耕地,荒地改造为Ⅰ类耕地的面积为58 hm2,修建水库的方案下,可充分利用水资源,发挥最大的经济效益。结合国民生产总值、粮食需求量、农业科技水平等社会因素,建立优化模型,农田水利建设规划方案不变。

