平面向量数量积课堂教学的反思与重构
程仕然

[摘 要] 文章对向量数量积课堂教学中内容衔接问题、物理背景引入问题和如何发展学生抽象素养问题进行反思. 在反思的基础上,重塑概念产生的过程,发展学生数学抽象素养,“落实四基,发展四能”来进行课堂重构,并对课堂教学进行实录.
[关键词] 课堂教学;反思;重构;向量数量积
问题研究缘起
我校特级教师蒋智东老师曾上过一节“平面向量数量积”的公开课,并写了篇实录及反思文章[1](下称文1),至今仍被同行所津津乐道. 今年笔者在上这节课前,向蒋老师进行了请教和交流.蒋老师认为,新的课程标准更关注数学学科核心素养的形成和发展,更重视学生学习的过程. 所以,上过的那节课还有很多地方需要反思改进,建议重塑概念产生的过程,发展学生数学抽象素养,本着“落实四基,发展四能”来进行重构.
关于本节教学内容的若干反思
针对本节内容,笔者再次认真学习了教材,学习了课程标准.结合蒋老师的文1,重点对向量知识板块的内部衔接及数学文化渗透、物理背景引入、如何培养数学抽象素养等方面进行了反思和研究.
1. 关于向量知识板块的内部衔接及数学文化渗透的思考
文1的“情景创设”部分:
问题1:物理学中,向量的运算比较多,比如求位移、速度、合力的大小等,用到了向量的加法、减法和数乘运算,那么,物理中还有没有其他的向量运算呢?
设计意图:本课通过物理学中的求功运算来创设教学情景,使学生自然提出问题:求功运算与数学知识有怎样的联系?
蒋老师紧扣课程标准,通过向量丰富的物理背景,从位移、速度、合力的大小等实际情境入手,理解向量的概念与运算法则,快速进入主题. 在实际的课堂教学中,这种方式是实用有效的,也是值得学习和借鉴的.
2. 关于教材向量数量积概念的物理背景引入的思考
在实际的教学实践中,向量这一部分内容往往放在高一下学期进行学习,课本上,这节课是以物理上功的运算这一物理模型进行引入展开的. 但这个时候学生物理上对功的学习也是刚刚展开,并且物理课本上是这样介绍功的:用F表示力的大小,用l表示位移的大小,用W表示力F所做的功,……,当力F的方向与运动方向成某一角度(α),……,所以W=Flcosα,这就是说,力对物体所做的功,等于力的大小、位移的大小、力与位移夹角的余弦这三者的乘积[2].
用物理背景引入,存在物理学科描述和数学学科描述的符号及说法上的不同.如上面所说,物理中,用“F”表示力的大小,用“l”表示位移的大小,而没有用F和l表示,这在学习之初,多少给学生带来困扰.
3. 关于本节内容在课堂教学中培养数学抽象素养的思考
文1关于数学抽象部分:
问题4从求功的运算中,可以抽象出什么样的数学运算?
教师指出数学抽象的方向:舍弃抽象原型的物理意义,抽取其中的数量关系.
平面向量的数量积
(1)最初的认识
学生讨论:把力F和位移S抽象地看成两个向量a和b,把力F和位移S的夹角θ看作向量a和b的夹角,就可以得到一种新的运算,它是从向量a,b得到一个数量(即abcosθ)的运算.
(2)进一步表述
引进“向量的数量积”等术语后,就可以把上面的结果进一步表述为:
已知两个向量a和b,它们的夹角为θ,我们把数量abcosθ叫做a和b的数量积(或内积),记作a·b,即a·b=abcosθ.
蒋老师以问题驱动思考,步步深入,从物理“功”抽象出数学平面向量的数量积运算,实现概念的自主建构,也让学生领悟到数学的发展源于实践.这种学习方式是建立在从物理到数学的“联想”基础上的.
我们知道,数学抽象是指通过对数量关系与空间形式的抽象,得到数学研究对象的素养. 主要包括:从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,并用数学语言予以表征[3].
与前面所学的向量运算结果不同,向量的数量积的结果不再是向量而是数量,学生是首次接触像这样运算结果与运算对象不是同一范围的运算. 如果设计一个微探究,让学生自己在熟悉的数学内容中抽象出新的数学内容,让学生充分经历和体验“发现定义”的过程,领悟数学发展的内部需求,不是更能激发学生的探究兴趣和积极性吗?
向量数量积课堂教学重构
1. 向量数量积课堂教学重构的指导思想
(1)重塑概念产生的过程,发展学生数学抽象素养,“落实四基,发展四能”;
(2)多一点数学文化熏陶,多一点数学本质探索,多一点数学素养培养.
2. 重构后向量数量积课堂教学实录
师:同学们,通过前面的学习,我们知道向量兼具“数”与“形”的双重形态,是沟通几何与代数的桥梁. 其实,前面,我们已学习了向量的概念及表示、线性运算和坐标表示,这些内容的产生和发展经历了漫长的时间. 大致可以分为三个阶段:向量1.0原始版:古希腊的亚里士多德已经知道两个力的合成,可以用平行四边形的法则得到,这点向量知识,形成不了多少有意义的问题,只是向量的原始萌芽形态[4]. 向量2.0社会版:牛顿第一次用有向线段表示向量;平面向量基本定理的出现,使得向量可以用两个非零向量进行分解,形成了一簇向量,相当于一个社会. 向量3.0高科技版:當时间进入十九世纪时,哈密尔顿引进新运算,沟通了代数、几何与三角函数,诸多几何问题都可以用向量方法“一揽子”解决了,向量进入了“高科技时代”.
我们将通过下面的学习来揭开“高科技版”的面纱.
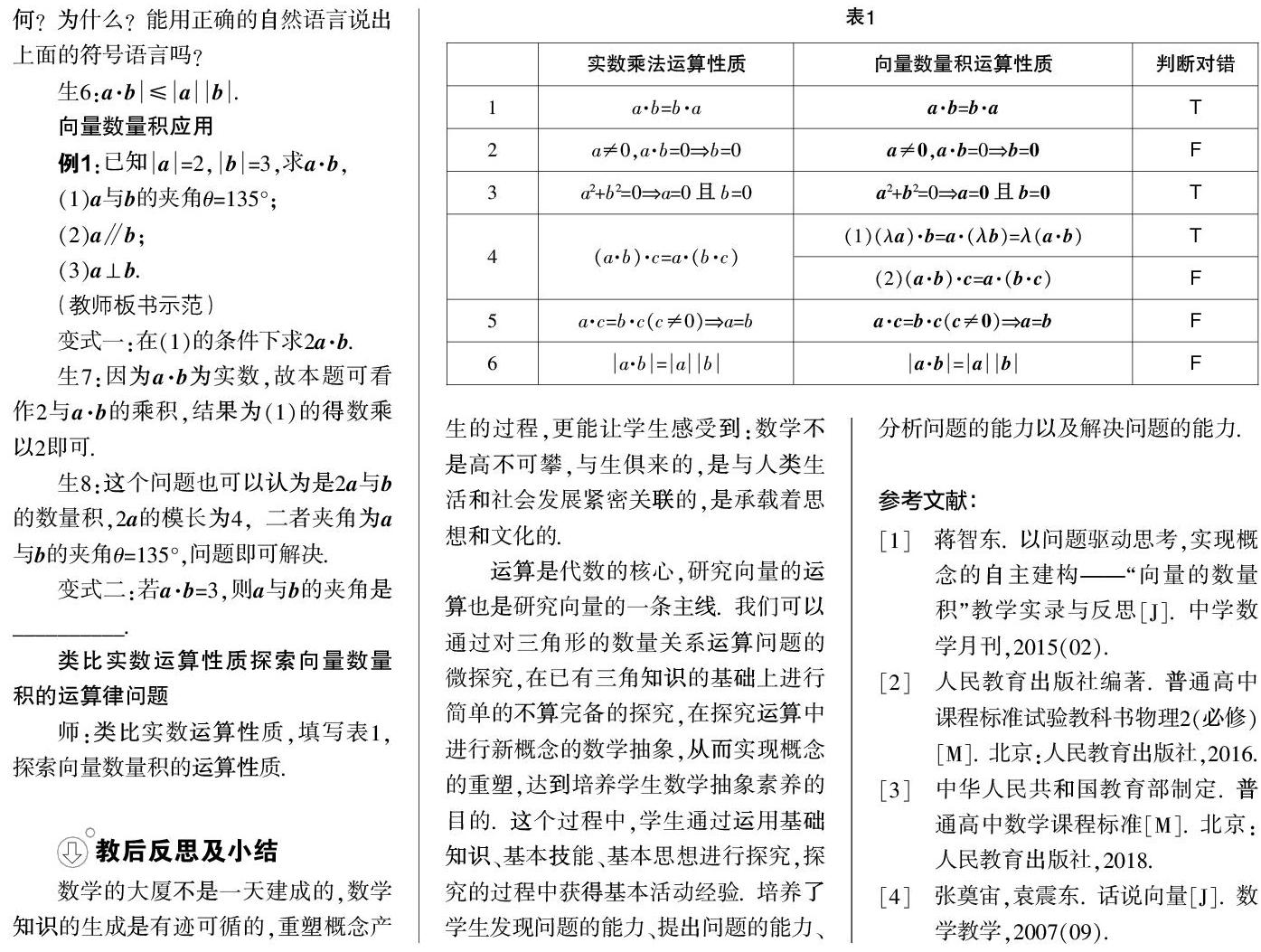
师:类比实数运算性质,填写表1,探索向量数量积的运算性质.
教后反思及小结
数学的大厦不是一天建成的,数学知识的生成是有迹可循的,重塑概念产生的过程,更能让学生感受到:数学不是高不可攀,与生俱来的,是与人类生活和社会发展紧密关联的,是承载着思想和文化的.
运算是代数的核心,研究向量的运算也是研究向量的一条主线. 我们可以通过对三角形的数量关系运算问题的微探究,在已有三角知识的基础上进行简单的不算完备的探究,在探究运算中进行新概念的数学抽象,从而实现概念的重塑,达到培养学生数学抽象素养的目的. 这个过程中,学生通过运用基础知识、基本技能、基本思想进行探究,探究的过程中获得基本活动经验. 培养了学生发现问题的能力、提出问题的能力、分析问题的能力以及解决问题的能力.
参考文献:
[1] 蒋智东. 以问题驱动思考,实现概念的自主建构——“向量的数量积”教学实录与反思[J]. 中学数学月刊,2015(02).
[2] 人民教育出版社编著. 普通高中课程标准试验教科书物理2(必修)[M]. 北京:人民教育出版社,2016.
[3] 中华人民共和国教育部制定. 普通高中数学课程标准[M]. 北京:人民教育出版社,2018.
[4] 张奠宙,袁震东. 话说向量[J]. 数学教学,2007(09).

