基于Kendall重现期的华南中小流域洪水峰量联合分布研究

赵玲玲, 杨 兴, 刘丽红, 刘昌明

(1.广东省遥感与地理信息系统应用重点实验室, 广东 广州 510070;2.广州地理研究所 广东省地理空间信息技术与应用公共实验室， 广东 广州 510070；3.广州地理研究所， 广东 广州 510070； 4.中国科学院 地理科学与资源研究所， 北京 100101；5.安徽理工大学 地球与环境学院， 安徽 淮南 232000； 6.北京师范大学 水科学学院， 北京 100875)

水文极端事件的风险概率及其相应的重现期标准是当前设计洪水计算中迫切需要解决的重要科学与工程应用问题。受亚热带季风性气候影响，华南地区天气系统复杂中小尺度天气系统十分活跃，汛期降雨具有强度大，季节性强，时间短、范围小、致灾性重等特点[1]，山区地貌陡峻，河道坡降大，山洪灾害频发。在气候变化背景下，山区中小流域增大了极端降水频率与强度，产生的山洪灾害已成为防灾减灾的重点[2]。研究年内洪水最大洪峰和洪量的分布类型和重现期，均可为防洪工程的建设和优化提供依据。但是单变量频率的分析并不能满足洪水多个特征属性的特点，且变量之间存在相依性，因此同时考虑洪峰和洪量两个洪水特征之间的联合频率，对流域洪水特征的分析是一个重要的研究方面。近年来，对洪峰、洪量和洪水历时等多变量联合分析受到关注[3-11]，其中Copula函数能够灵活的联结两变量或多变量的水文因子联合分布，在水文变量分析中得到广泛的应用。Nelson[12]总结了Copula相关研究领域的主要成果，谢华等[13]对水文频率研究中二维联合概率采用的4种阿基米德族Copula函数及其综合选优做了述评。侯芸芸等[14]、陈子燊等[9]应用Copula函数，探讨洪水三变量的联合概率分布和条件概率分布，验证了Copula函数可以在三维洪水变量中的适用。郭生练等[15-16]对多变量水文分析计算中的应用与研究进展作了述评，指出对于给定的重现期如何合理地选择联合设计值是关键问题。

目前联合频率分析多集中在对两要素的“或”和“且”重现期上，Salvadori等[17]和有关研究[9,15]表明使用Copula函数计算多变量“或”联合重现期和“且”联合重现期十分简便，可为风险分析提供一种非常简单而又有效的方法。但“或”联合重现期和“且”联合重现期在危险域或安全域划分上存在局限性，Salvadori等[18]等引入了一个新的可与特定事件联合重现期相关联的分布函数——Kendall测度，并定义了一个新重现期Kendall重现期，其涵义为超过阈值事件的平均到达时间(临界事件)。相比于传统重现期，Kendall联合重现期的提出改进了多变量联合设计的可靠性[19]，为处理潜在危险(破坏性)的随机事件的频率分析领域提供了新的研究途径，Corbella S等[20]等在海岸侵蚀中进行了应用；陈子燊等[8]在城市洪涝中基于Kendall重现期推算的不同历时暴雨组合的设计暴雨分位值，验证了Kendall重现期优于传统的重现期；刘章君等[21]考虑了洪峰、洪量与水库调洪规则的交互作用中发现Kendall和生存Kendall重现期也存在不同程度的偏低或偏高；范嘉炜等[22]、史黎翔等[23]在城市洪涝、无定河流域中应用研究，也验证了Kendall重现期的合理性。但是对于山区中小流域山洪特点下Kendall重现期的相关研究存在不足，能否适用于山区中小流域洪水设计工程中还有待研究。因此，本文拟通过对华南三个山区中小流域的洪峰和洪量联合分布的实例，分析“或”重现期、“且”重现期和Kendall重现期的设计水平之间的差异，以期为多变量洪水频率分析在山区洪水中的应用提供理论参考。

1 理论与方法

1.1 Copula函数

Copula理论指出多个变量的联合分布可分解为多个不同的边缘分布，通过一个Copula函数构建联合分布。据此理论，设(x,y)为二维随机变量，u=FX(x)，v=FY(y)为连续的边缘分布函数，则有唯一的Copula函数C使得：

F(x,y)=P(X≤x，Y≤y)

=C〔FX(x)，FY(y)〕=(u,v)

(1)

式中：F(x,y)为联合分布函数，关于Copula函数性质的更详细描述可参阅Salvadori等(2007)[24]的论述。

1.2 重现期定义

(2)

(3)

式中：μ——两个连续事件的平均到达时间。

1.2.2 Kendall分布函数与Kendall重现期 从“或”和“且”重现期可知，相同的累积频率均可产生相同的重现期，不会因u，v组合事件的不同而改变。为解决由“或”和“且”重现期存在的对安全事件与危险事件错误的识别，又将其分为亚临界(安全域)、临界(警戒事件)和超临界(危险域)3种情景[24-25]。通过判定累积概率不超过某临界概率，将多维的极值事件投射为一维分布，完全区分了安全事件与危险事件在空间域的分布。黄强等[11]对此作了详细的图解说明。与Copula函数累积概率为t的(u,v)组合值相关联的Kendall测度KC为：

(4)

式中：φ(t)为KC生成元；φ′(t)为φ(t)的右导数。由Kendall测度确定的重现期称为Kendall重现期(TKEN)：

(5)

Graler等[26]对二维Copulas的“或”、“且”和Kendall重现期三种联合重现期(JRP)的不等关系作了图示解释(图1)：对于一固定的设计事件(u,v)，其累积分布单位平方图内不同的重现期TOR，TKEN和TAND可以用1/(1-面积(安全事件))表示。如图1所示，“或”重现期定义仅将左下角矩形中的所有事件视为安全的。Kendall重现期将左上角和右下角的曲线区域(KEN)与左下角的矩形区划为安全域，从而使同一设计事件(u,v)产生的重现期比“或”重现期更大。“且”重现期则进一步添加了左上角和右下角的矩形，从而得到最大的重现期。由式(2)—(5)和图1可知“或”、“且”和Kendall重现期之间的不等关系为：TOR≤TKEN≤TAND。

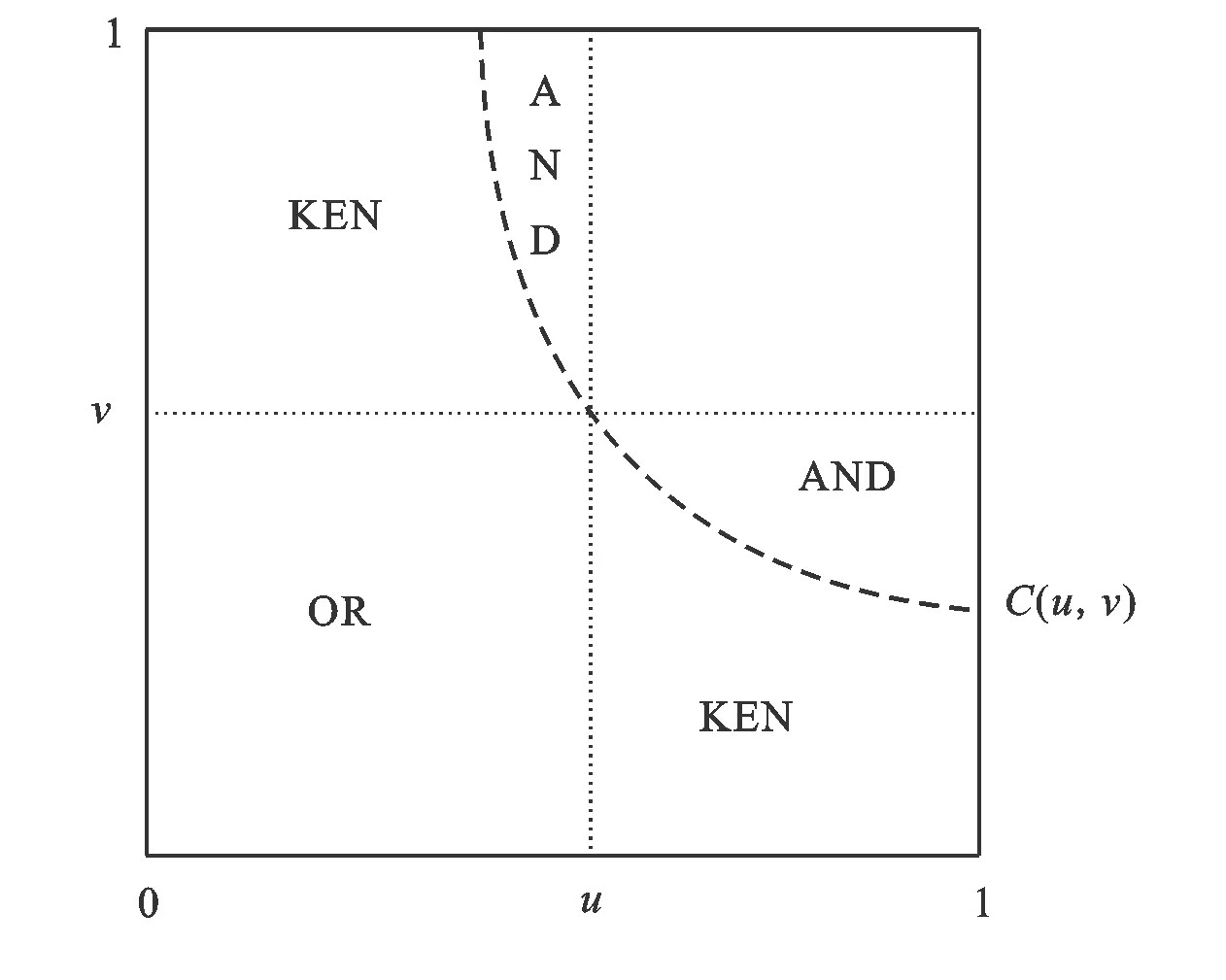
注：(u,v)为某一设计事件；C(u,v)为Copula水平曲线；KEN为Kendall重现期定义的安全域；AND为And重现期定义的安全域；OR为or重现期定义的安全域。

图1 3种联合分布重现期定义的图示说明[26]

1.3 水文特征设计值

由概率论，Q≥q条件下W≥w的累积概率分布为:

P(W≥w|Q≥q)=

(6)

此条件概率属于超值概率，可定义为遭遇概率。分析二者的遭遇概率有助于进一步认识流域洪水事件的统计规律，对于防洪管理决策具有重要的参考意义。

由于对某预定的重现期存在无数个满足防洪标准的多变量分位值组合，如何合理地推算联合设计值的问题成为一个关键问题[15]。有关研究指出，在重现期分位值相同情况下，必然存在一个组合值使得联合概率密度达到最大值，可利用以下公式推算联合分布设计值：

(7)

f(u,v)=c(u,v)f(u)f(v)

(8)

式中：(um,vm)为两变量联合概率密度 达到最大值时的组合设计值；f(u)，f(v)为边缘分布的概率密度函数；c(u,v)为二维Archimedean Copula的概率密度函数。

2 实例分析

2.1 流域概况

本文选取广东省中小流域曹江、田头水和罗坝水流域作为研究区，各站点位置为大拜水文站E111°09′N22°03′，结龙湾水文站E114°11′N24°54′，赤溪水文站E113°08′N25°03′，其中田头水流域只有广东省内水系。3个流域均为山区中小流域，地形崎岖、河流坡度大并且人为影响较小，其中曹江流域是广东省三大暴雨中心，出口断面大拜水文站集水面积394 km2，流域多年平均年雨量可达2 160 mm，最大平均年雨量达3 150 mm。赤溪水文站位于广东乐昌市庆云镇赤溪，是珠江流域北江水系武江支流田头水流域的控制站，集水面积为396 km2。结龙湾水文站是珠江流域北江水系一级支流墨江下游罗坝水流域的控制站，集水面积81 km2，流域多年平均年径流量2.75×108m3。

本研究分别收集了大拜水文站1967—2013年、赤溪水文站1967—2016年、结龙湾水文站1967—2016年场次洪峰流量数据。依据超定量法[27]，首先根据3个水文站枯水年最大洪峰流量为最小阈值，然后按各场洪水流量过程线提取洪峰流量并计算出该场洪水的洪量与历时，并剔除较差线型的洪水样本。为保证不同洪水之间的独立性，各场次洪峰发生的时间间隔要求大于流域汇流时间。3个流域分别抽取了231，169，264场洪峰流量和相应洪量作为峰量联合分布的分析样本。

根据洪水流量过程线(图2)提取洪峰流量Q(m3/s)、洪水历时D(天)和洪水总量(洪量)W：

D=te-ts

(9)

(10)

式中：ts为洪水开始时间；te为洪水结束时间；q为日流量序列。

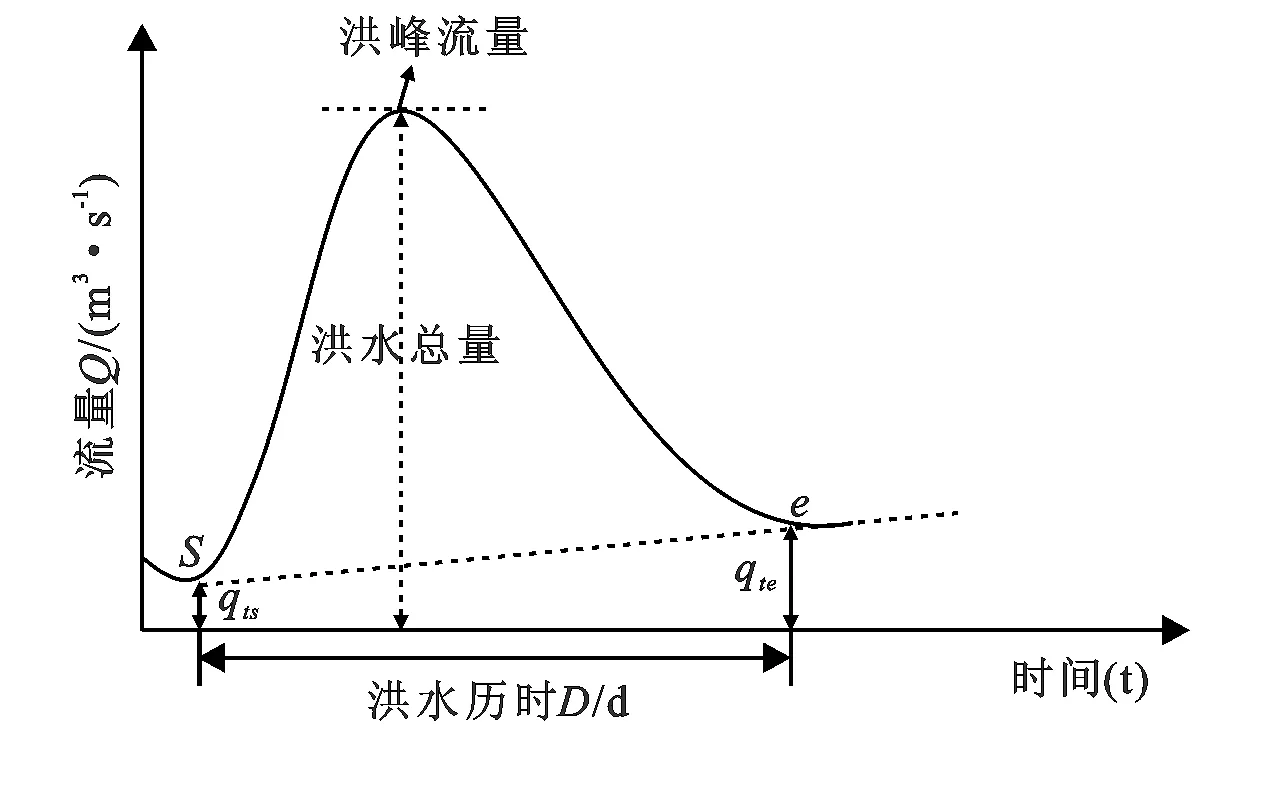
注：S，e为洪水基流切割点；qte为洪水开始点流量；qts为洪水结束点流量；Q为流量；D为洪水历时。

图2 洪水过程及相应的洪量与历时

2.2 Copula函数的选取

根据3个水文站多年洪水流量数据，用水文频率分析中常用的4种三参数概率分布：对数正态分布(GNO)、广义极值分布(GEV)、广义Logist(GLO)分布和皮尔逊三型分布(P-Ⅲ)，使用较稳健的线性矩方法[28]，分别对洪峰流量和洪水总量样本加以拟合。并对4种参数拟合的结果采用均方根误差(RMSE)和概率点据相关系数(PPCC)检验其拟合优度选择最优水文频率分布函数，拟合结果见表1。大拜站洪峰洪量序列宜选用GNO分布，赤溪站分别选用GLO分布和GEV分布，结龙湾站分别选用GLO分布和P-Ⅲ分布。

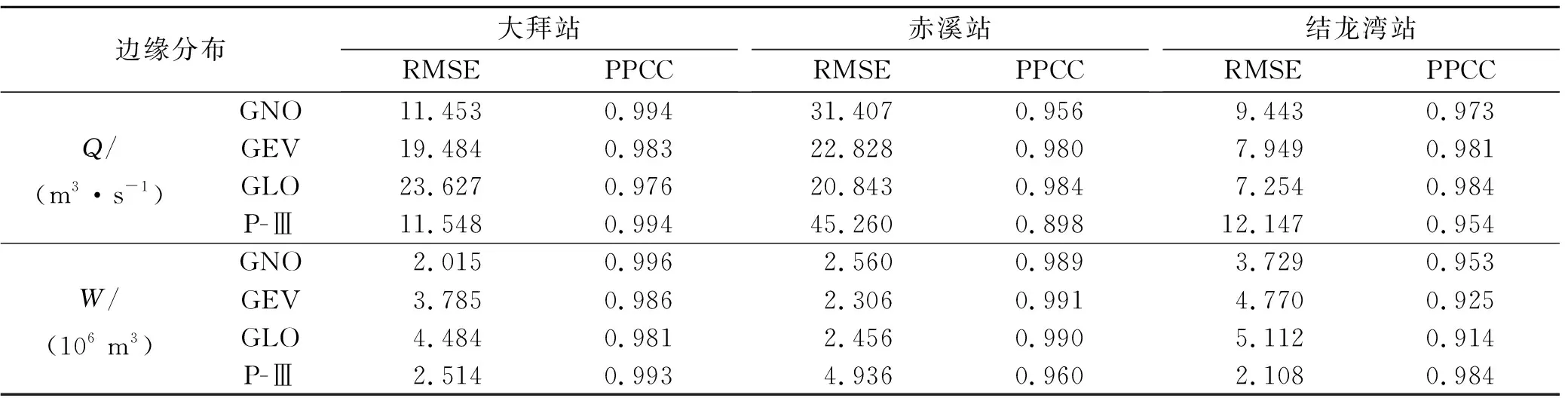
表1 3个流域洪峰和洪量的概率分布参数与拟合优度检验值

注：GNO为对数正态分布；GEV为广义极值分布；GLO为广义Logist分布；P-Ⅲ为皮尔逊三型分布；RMSE为均方根误差；PPCC为概率点据相关系数。

计算洪峰流量和洪水总量之间的Kendall相关系数，得到大拜水文站、赤溪水文站和结龙湾水文站的洪峰Q和洪量W的Kendall相关系数分别为0.79，0.80，0.76，表明洪峰流量和洪水总量之间具有较强的相关性。

采用基于秩相关的Kendall相关系数的计算洪峰Q和洪量W联合分布的4种阿基米德Copula参数θ，并采用Akaike信息准则法(AIC)和最小二乘法准则(OLS)确定结果(见表2)，可见4种Copula函数拟合结果较好，依据AIC和OLS结果选择最优Gumbel Copula函数来构建3个流域洪峰Q和洪量W的联合分布函数，各站构建的Copula分布模式如下：

大拜站：C〔FQ(q),FW(w))〕=exp{-〔(1-lnFQ(q))4.703+(-lnFW(w))4.703〕1/4.703

(11)

赤溪站：C〔FQ(q),FW(w))〕=exp{-〔(1-lnFQ(q))4.967+(-lnFW(w))4.967〕1/4.967

(12)

结龙湾站：C〔FQ(q),FW(w))〕=exp{-〔(1-lnFQ(q))4.142+(-lnFW(w))4.142〕1/4.142

(13)

表2 4个Copula函数的参数及其拟合优度指标

注：OLS为最小二乘法准则，AIC为信息准则法，θ为参数。

2.3 条件概率分布

洪峰流量和洪水总量都属于洪水过程的随机变量，在最大洪峰流量Q和最大洪水总量W都属于洪水过程的随机变量，估计出洪峰Q和洪量W之间的联合分布函数之后，就可以推求出给定某种事件发生概率的条件下的另一种事件发生的概率。分析特定设计洪峰流量条件下出现洪水总量的概率分布，由公式(6)可以求出洪峰洪量条件概率值。

根据洪峰洪量条件概率结果(见表3)，3个流域出现概率大于等于表中概率的洪峰流量时，洪水峰量同频率遭遇概率很大，且由于洪峰洪量具有高相关性，还有很大可能出现洪峰遭遇更小频率的洪量。其中，曹江流域大拜站峰量同频率遭遇大于84.1%，主对角线以上二者遭遇的概率则大于98.4%；田头水流域赤溪站峰量同频率遭遇大于85%，主对角线以上二者遭遇的概率则大于98.7%；罗坝水流域结龙湾站峰量同频率遭遇大于81.8%，主对角线以上二者遭遇的概率则大于97.3%。

由以上分析可见，此3个流域洪水峰量的遭遇风险概率基本接近，当洪峰大于或等于某一设定频率时，洪量出现大于该频率的条件概率随之增大。上述结果表明洪水峰量联合分布可能存在着多种结果，分析多种组合出现的不同遭遇概率有利于现实中防汛减灾的风险管理。

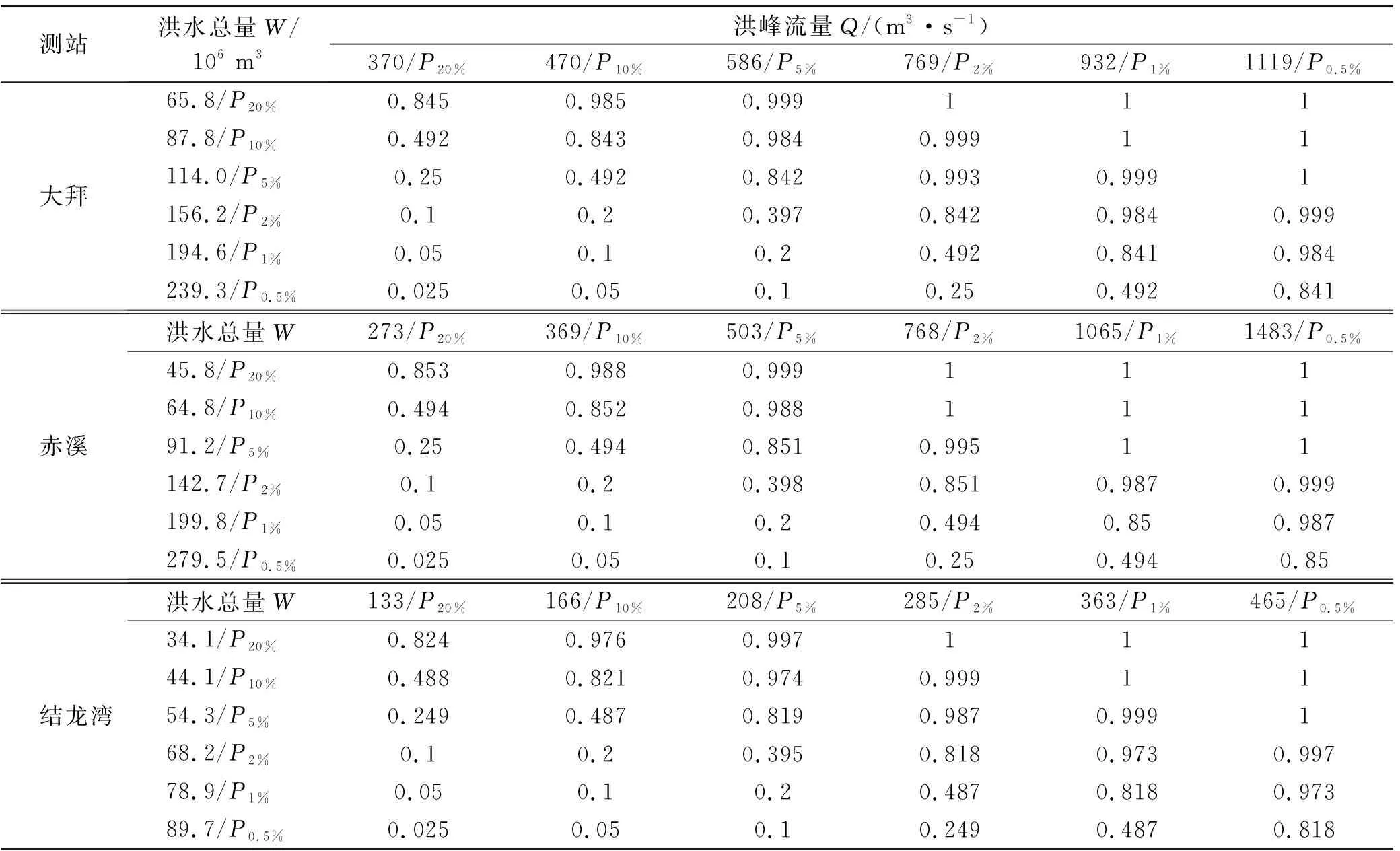
表3 华南中小流域洪峰洪量条件概率〔P(W≥w|Q≥q)〕

2.4 联合分布重现期

采用Gumbel Copula联结函数根据式(7)求洪峰Q和洪量W组合的“或”、“且”和二次重现期结果(见表4)。从3个流域洪水峰量联合分布计算结果可看出，对于特定的设计重现期，Kendall重现期都介于“或”和“且”重现期之间，并且大于设定重现期。“或”联合重现期最小且小于设定的重现期，“且”重现期最大且大于设定的重现期。“或”、“且”和二次重现期联合分布重现期与特定的设计重现期之间两者的相对为误差为，TOR：-0.12%～-0.15%，TAND：0.16%～0.22%，TKEN：0.08%～0.11%。Kendall重现期联合分布设计值最为接近设定重现期，对洪水峰量之间任一要素超标致灾的重现期标准宜采用Kendall重现期。3种联合重现期较为接近，或与此3个中小流域同处华南气候区，洪水事件具有相近的背景有关。

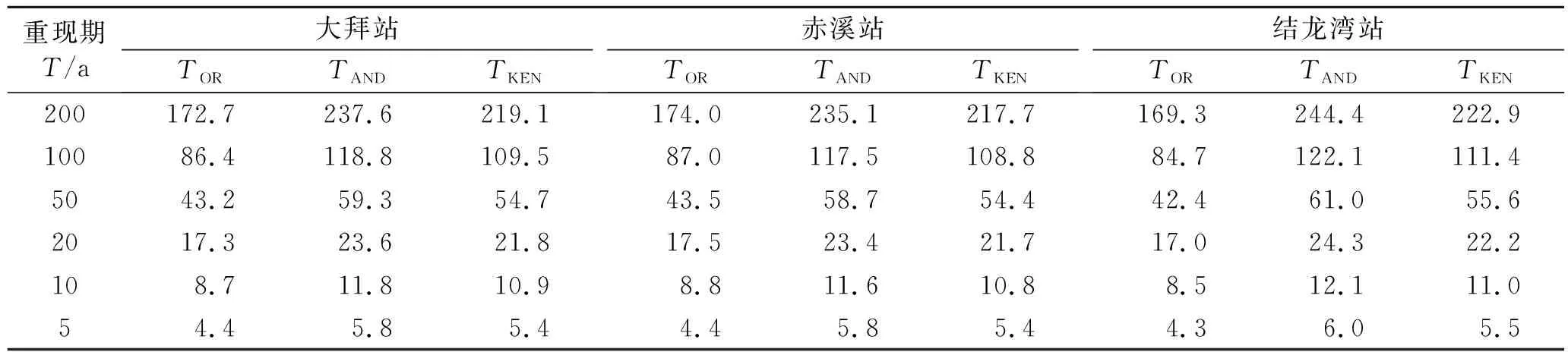
表4 华南中小流域洪水峰量联合分布的重现期

2.5 设计洪水分位值

根据重现期计算方法的不同，分别求设定重现期下各水文站的洪峰流量和洪水总量单变量设计值列于表5。分析表5中3个流域不同重现期下洪峰流量与洪水用量的设计值特征，可以得出以下结论。

(1) 对于设定的重现期，3个流域的单变量设计洪峰流量和设计洪水总量及其联合设计值，以赤溪站最大，大拜站次之，结龙湾站最小。虽然赤溪站所在的田头水流域和大拜站所在的曹江流域集水面积大致相同，但主要与田头水流域2006年7月14—15日2 d内遭遇652.5 mm特大降雨形成的超百年一遇大洪水有关。

表5 3个流域不同重现期下洪峰流量与洪水总量的设计值

注：Q为洪峰流量(m3/s)；W为洪水总量(106m3)。

(2) Kendall重现期推算的值小于“或”重现期设计值和边缘分布推算的设计洪峰流量和设计洪水总量设计值，两者的相对为误差为，大拜站：洪峰流量:-0.7%～1.1%，洪量:-1.3%～0.7%；赤溪站：洪峰流量:-4%～0.4%，洪量:0%～3%；结龙湾站：洪峰流量:-5.9%～-3.4%，洪量:-2.2%～-0.1%。

上述结果表明，Kendall重现期推求的设计洪水值大于洪水、峰量边缘分布设计值，并介于“或”和“且”重现期设计值之间。与表4联合分布结果一致，因此Kendall重现期可以作为洪水峰量联合分布的待选方法，为防洪工程安全与风险管理提供更好的选择。为进一步比较分析，推算洪峰洪量同频率分布设计值[29]：

u1=u2=〔1-(1-Tu1,u2)〕α；

Q=F-1(u1)；W=F-1(u2)

(14)

式中：α=2-1/θ；Tu1,u2为“或”重现期；F-1(ui)为边缘分布函数的反函数。

3个流域不同重现期下洪峰流量与洪水总量的设计值(见表5)，进一步比较分析洪水峰量联合分布的同频率设计值和联合概率密度最大值推算的重现期设计值，可以看出设定重现期下两者设计值十分接近，并且均低于“或”重现期设计值。表明了对于工程设计来说“或”重现期或同频率分布设计值存在“高估”的问题，会提高水工建筑建设成本。

一场洪水的造成的损失并不是单个特征变量决定的，而是多个洪水特征变量共同作用的结果，例如同一量级的洪水并不一定造成同样的影响，不同大小的洪量也可能导致同样程度的破坏，因此多变量联合分布的研究十分重要。其中一个重要方面是变量之间的建模，Copula联结函数在多元洪水特征分析方面的潜力；另一个重要方面是重现期方法的选取，不同方法的选择直接影响到建造结构的安全和成本。相对于传统重现期，Kendall重现期设计值介于“或”与“且”重现期之间，且略高于设计重现期。Kendall重现期在工程安全设计理念高于“或”重现期设计值，对于工程经济理念来说高于“且”重现期设计值。上述洪峰和洪量的Kendall相关性较高，且主对角线上条件概率超过81%表明洪水峰量联合分布存在多种结果。由表4和表5分析可知，Kendall重现期在3个流域有较好的应用结果。且黄强等[11]研究也表明传统的“或”和“且”多变量重现期对安全与危险域的识别具有局限性。因此，可以说明，Kendall重现期在洪水峰量联合分布计算中优于传统重现期，可以为山区中小流域防洪工程安全提供更多的选择。

3 结 论

本文对比分析了广东省中小流域曹江、田头水和罗坝水流域洪峰洪量之间的联合分布及其重现水平，有以下结论：

(1) 由4种累积分布函数择优构成了3个流域不同的洪水峰量联合，AIC和OLS拟合结果表明使用Gumbel Copula构建了最佳的洪峰洪量联合分布;洪峰Q和洪量W的Kendall相关系数分别为0.79，0.80，0.76,表明洪峰流量和洪水总量之间具有较强的相关性。

(2) 作为山区暴雨洪水成因的洪水过程,3个流域洪水峰量相关性高,主对角线以上的条件概率超过81%,洪水峰量遭遇风险概率大且基本接近,分析多种洪水峰量组合出现的不同遭遇概率有利于防汛减灾的风险管理。

(3) 相对于“或”重现期,采用Kendall测度计算的Kendall重现期可更好地区分超临界事件的风险率。Kendall重现期推算的洪峰洪量设计洪水值介于“或”重现期与“且”重现期设计值之间,接近于边缘分布设计值。在经济安全方面,Kendall重现期设计洪水更优于传统重现期设计方法,可为防洪工程风险管理与设计提供新的选择与参考依据。