风电机组风向波动概率特性研究

宋 鹏，柳 玉，郭 鹏，徐金晖

（1.华北电力科学研究院有限责任公司（国网冀北电力有限公司电力科学研究院），北京 100045； 2.华北电力大学 控制与计算机工程学院，北京 102206）

0 引言

近年来，随着风电新能源补贴的减少和平价上网政策的推进，各大风电企业对风电机组的要求也从“能发电”向“多发电”转变。 优化风电机组的运行与控制，提高单机发电量具有重要意义。风电机组的能量来源是风，机组所处地理位置的风资源是影响其发电效率和性能的最重要因素。

由于地理位置和地形的差别，同一风电场中的不同机组的本地风资源存在很大差别。 定量精确分析风电机组本地风资源特性，根据风资源特性有效指导风电机组控制系统的个性化参数优化设置，使控制参数与机组本地风资源匹配，能够改变目前同一风电场中同一型号机组运行和控制参数完全相同导致的某些机组发电效率偏低的现状，提高风电场的运行管理水平和经济效益。

关于风向波动特性，文献[1]，[2]认为自然风向密度遵循高斯分布。 文献[3]提出了风速波动系数和风向波动系数，定性描述了风的波动对功率波动的影响。 文献[4]对风向数据进行了统计，但仅分析了风向总体上的分布范围特点，缺乏关于风向波动特点的衡量指标。

风向波动与风电机组偏航系统密切相关[5]，[6]。风向与机舱轴线的夹角为偏航误差，偏航控制系统在风向发生改变时，通过位于机舱和塔架连接处的偏航电机带动整个机舱和叶轮向风向标指示风向转动，消除偏航误差，实现叶轮对风。 定量研究风电机组本地风向波动特性对优化其偏航控制系统参数具有重要指导作用。

本文在第一节中提出了风向波动量的定义方法； 在第二节和第三节中对风向波动量的边缘分布和联合分布进行了求解； 在第四节中分析了风向波动量联合分布参数与风向波动特点之间的关系，采用概率分布参数对风电机组本地风向波动特性进行精确量化描述。

1 风向波动量的定义方法

本文使用的风资源数据为云南某风电场每台机组自身风速计和风向标采集的风资源数据。 偏航系统通常有偏航误差阈值和偏航误差持续时间阈值两个控制参数。 当机组检测到偏航误差角度大于偏航误差阈值，且这种状态超过持续时间阈值时，偏航系统对风开始。该风电场机组偏航系统的两个控制参数分别为10°和30 s。 由于偏航系统的持续时间阈值参数为秒级，因此，本文采用的风资源数据采样周期为1 s。由于风向角度变化具有较强随机性，仅观察分析风向时序变化难以挖掘风向波动的有效信息。 本文对风电场大量秒级风资源数据进行分析研究，提出了基于风向波动幅值-波动持续时间的风向波动定量描述方法。

1.1 风向波动幅值-持续时间定义方法

选取一段时间长度为40 s 的秒级风向序列（图1）。 将风向角度持续上升或者持续下降的一个完整过程记为一次风向波动，风向角度持续增大记为正向波动，风向角度持续减小记为负向波动。 每次风向波动均有两个波动参数即波动幅值（A）和波动持续时间（T）。 图1 中，矩形框圈选的一个正向波动的两个参数分别为A=10°和T=2 s，圈选的一个负向波动的两个参数分别为A=22°和T=4 s。

图1 正向波动和负向波动的定义Fig.1 Definition of positive and negative fluctuations

1.2 秒级风向波动量

选取某台机组一个较长时段的秒级风向序列，按上述风向波动量的定义统计其风向波动次数、 每一次风向A 和T。 得到一组风向波动量序列，即一组二维随机变量（A，T），每一个二维随机变量为一次风向波动的两个参数。 二维随机变量（A，T）的性质不仅与随机变量 A 和 T 有关，还依赖于这两个随机变量的相互关系。

二维随机变量（A，T）的分布函数为

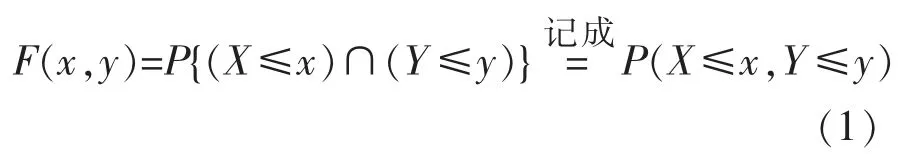
式中：x，y 为任意实数。

风向 A 的取值范围为 （1 °，2 °，3 °，…），T 的取值范围为（1 s，2 s，3 s，…）。

记二维离散型随机变量（A，T）的所有可能取值为（ai，tj），i，j=1，2，…，其中，ai∈（1 °，2 °，3 °，…） ，tj∈（1 s，2 s，3 s，…）。 则二维离散型随机变量（A，T）的分布律为

以该风场A03 机组某时段风向序列为例，其二维离散型随机变量 （A，T） 的分布律如图2 所示。 当风向波动幅值较小，持续时间较短时，对风电机组的输出功率影响很小 （偏航误差为θ=2°，功率损失约为0.183%），因此，图2 中仅统计幅值大于2°，持续时间大于2 s 的风向波动。

图2 二维离散型随机变量（A，T）的分布律Fig.2 Distribution law of two-dimensional discrete random variables（A，T）after removing small fluctuations

2 二维风向波动量（A，T）的边缘分布概率密度函数

为求得风向波动量（A，T）的联合概率分布，首先，须对其边缘分布进行研究。 选取风场A03和 A09 机组于 2018 年 3 月1 日至 8 日的秒级风向数据进行对比统计分析。 两台机组均为2 MW直驱机组。 按照1.1 中波动量的定义分离出二维随机变量（A，T），得到 A03 和 A09 机组的两组风向波动量。 在此时段，A03 机组的平均风速为6.4m/s，A09 机组的平均风速为6.5 m/s，两者非常相近。

2.1 二维风向波动量（A，T）关于A和T的边缘分布概率直方图

对已求得的关于A03 和A09 机组的秒级风向波动量（A，T）进行边缘分布概率密度的统计，并做出直方图（图3，4）。

图3 A 的边缘分布概率直方图Fig.3 Edge distribution histogram of fluctuation amplitude A

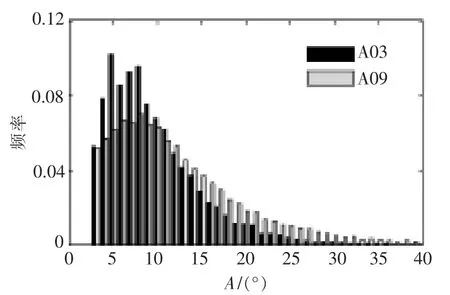
图4 T 的边缘分布概率直方图Fig.4 Edge distribution histogram of fluctuation duration T

由图3，4 可知：无论是A，还是T 的边缘分布概率直方图，A03 和A09 机组均有明显不同；A03机组波动幅值小，持续时间短的风向波动概率较A09 机组高，其短促多变的风向多；A09 机组持续时间长的风向波动概率显著高于A03 机组，持续稳定风向多。

2.2 Weibull风向波动边缘分布拟合

为抽取风向波动量边缘分布概率直方图的整体分布特征，采用适合风资源概率特性的Weibull分布对风向波动幅值和持续时间的边缘分布进行拟合，拟合方法为最大似然估计。

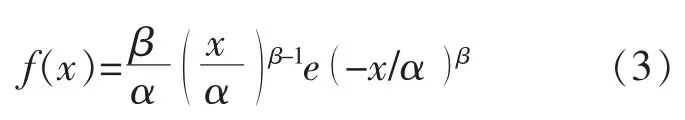
式中：α 为尺度参数；β 为形状参数。

Weibull 分布对A 的边缘分布概率密度函数拟合所得参数如表1 所示。

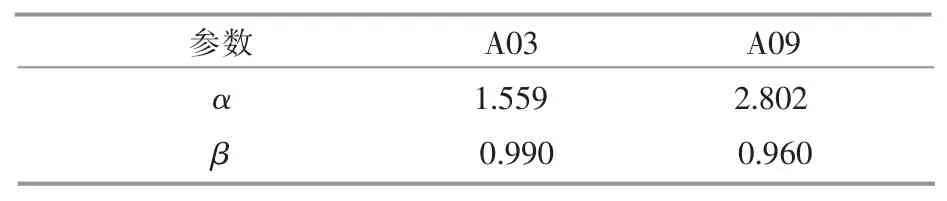
表1 A 的边缘分布拟合参数Table 1 Edge distribution fitting parameters for fluctuation amplitude A

A03 机组和A09 机组A 的边缘分布概率密度拟合函数如图5 所示。

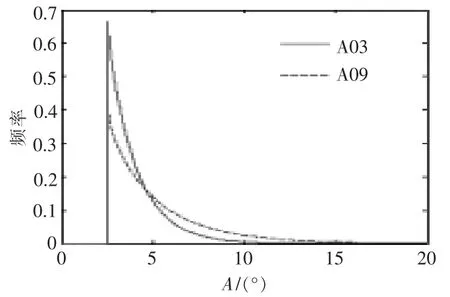
图5 A 的 Weibull 分布拟合Fig.5 Weibull distribution fit diagram for fluctuation amplitude A

Weibull 分布对T 的边缘分布概率密度函数拟合所得参数如表2 所示。

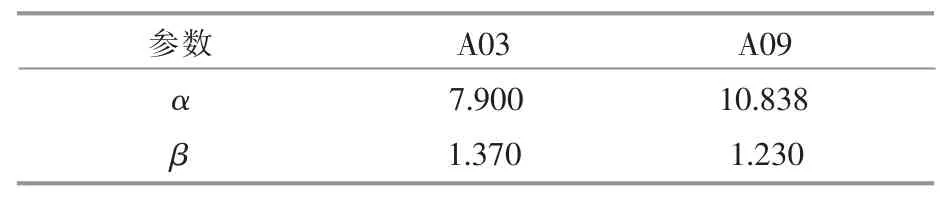
表2 T 的边缘分布拟合参数Table 2 Edge distribution fitting parameters for fluctuation duration T

A03 和A09 机组T 的边缘分布概率密度拟合函数如图6 所示。

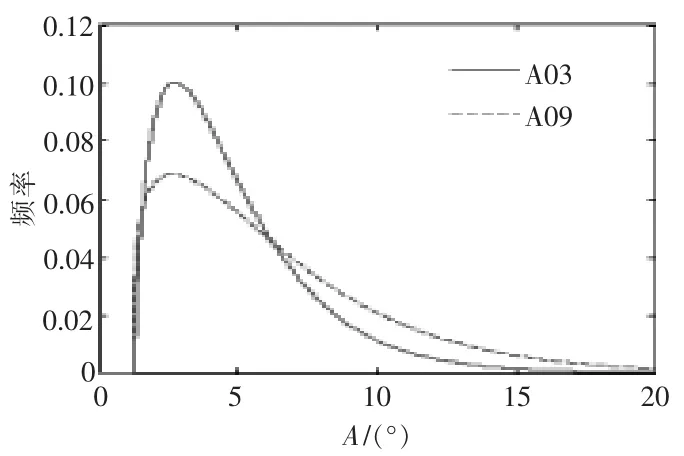
图6 T 的 Weibull 分布拟合Fig.6 Weibull distribution fit diagram for fluctuation duration T

Weibull 分布的β 主要决定拟合函数的形状。由表1 可知，形状参数βA均小于 1 且相近，图5中的分布函数均呈现指数分布形状。由表2 可知，形状参数βT均大于1 且相近，图6 中的分布函数均呈现“驼峰分布”形状。

Weibull 分布的α 主要决定拟合函数的陡峭程度：α 越大，概率密度分布越平缓，尾部占比越大；α 越小，概率密度分布越陡峭，尾部占比越小。 由表1 和表2 中的 α 可知，无论是 A 的 α ，还是 T 的 α ，A09 机组均大于 A03 机组。 由图5和图6 可知，A09 机组的拟合分布函数均呈现“胖尾” 特性，A03 机组的拟合分布函数则呈现“瘦尾”特性，与概率直方图相一致。

因此，通过连续Weibull 边缘分布概率拟合函数，风向波动幅值特征和持续时间特征可以简化为分别用尺度参数αA和αT表征。

3 二维风向波动量（A，T）的联合分布概率密度函数

完成二维风向波动量关于A 和T 的边缘分布拟合后，可对其联合概率分布进行分析。

Copula 函数是一种可以将多维随机变量联合分布函数与其各自的边缘分布函数连接在一起的函数[7]，[8]。

本文中风向波动量（A，T）的 A 和 T 的边缘分布函数已知，只要求得合适的二维Copula 函数，便可以得到风向波动量的联合概率分布函数。

Archimedean-Copula 具有结构简单、 应用广泛的特点，本文选取该函数簇Frank-Copula 函数。

设 u 和 ν 分别为二维随机变量（A，T）的两个边缘分布的概率密度函数，则Frank-Copula 函数的表达式为

式中：θF为相依参数，θF≠0，当 θF＞0 时，表示正相关，当 θF＜0 时，表示负相关。

选取Frank-Copula 函数求得的 A03 和 A09机组风向波动量的联合概率密度函数如图7所示。

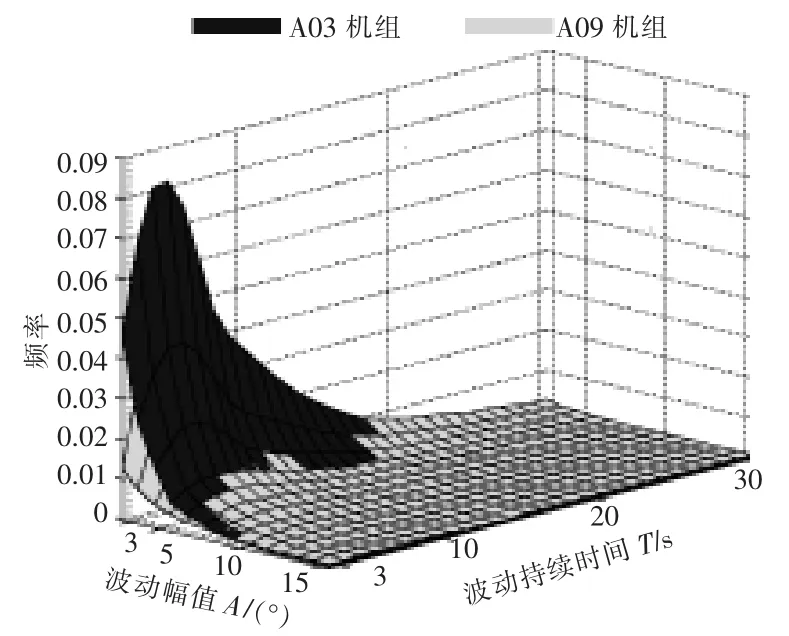
图7 A03 和A09 机组联合概率密度函数图对比Fig.7 Comparison of joint probability density function fit diagram of A03 and A09

由图7 可知： 当 A 和 T 都较小时，A03 机组的二维风向波动量（A，T）的联合概率密度比 A09 机组大，即 A03 机组 A 较小、持续时间短的细碎风向波动显著多于A09 机组，这种短促多变的风向既无法引发偏航系统对风，同时，使得偏航误差随时存在，导致机组捕获风能的能力下降，因此，A03 机组的风向稳定性差； 随着 A 和 T 的增加，A09 机组的二维风向波动量（A，T）的联合概率密度越来越大，超过A03 机组。 A09 机组 A 较小，而持续时间长的稳定风向，能够推动叶轮持续做功。 A09 机组A 大且持续时间长的显著风向波动将触发偏航系统对风，增加机组的风能捕获。 因此，A09 机组风向稳定性好。

为验证以上分析，对A03 和A09 机组研究时段，即2018 年3 月1 日至8 日期间的实际运行数据进行统计（表3）。 在此时段，两机组均未停机。

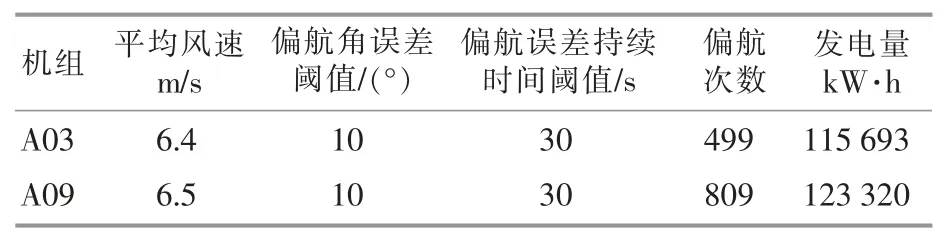
表3 发电量和偏航统计Table 3 Power generation and yaw statistics

由表3 可知：该时段A03 和A09 机组的平均风速相近，但A09 机组偏航809 次，显著多于A03 机组的 499 次，其发电量较 A03 机组多6.6%；A09 机组A 大、持续时间长，导致偏航系统动作的风向波动显著高于A03 机组。 与图7 的前述分析结论完全相同，验证了Copula 风向波动联合概率密度函数拟合的准确性。

4 风向波动特性与概率分布拟合参数关系

为简单直观量化风电机组本地风向波动的稳定性，从二维风向波动量（A，T）的联合概率密度函数中抽取一组参数。

①A 的边缘分布概率密度函数中的尺度参数 αA。

②T 的边缘分布概率密度函数中的尺度参数αT。

③ 稳定风向波动量概率百分比Pstable。A 较小（小于设定阈值EA）且 T 较长（大于设定阈值 ET）的波动量（A，T）代表持续稳定风向，其概率百分比Pstable越大时，说明该机组风向稳定性越好。

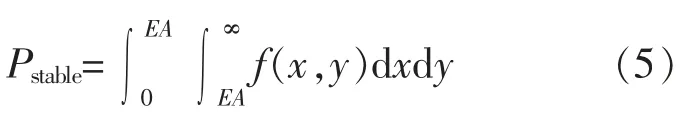
式中： f（x，y）为二维Copula 风向波动量（A，T）的联合概率密度函数。

当偏航误差超过10°，且时间持续30 s 以上时，触发偏航，故设定 EA=10°，ET=30 s。

表4 为A03 和A09 机组的参数值。

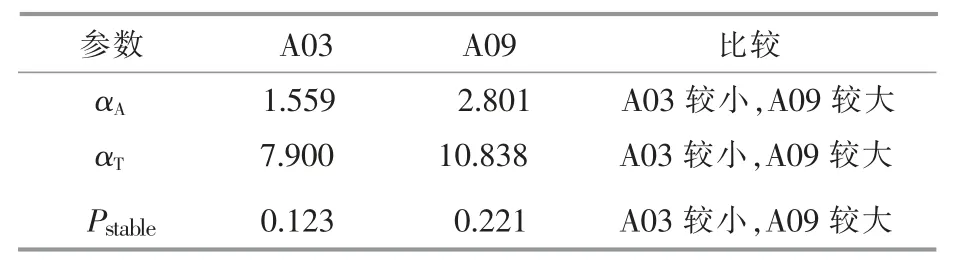
表4 A03 和A09 机组的参数值Table 4 Parameter values of A03 and A09

由表4 可知： 风向较稳定的 A09 机组的Weibull 边缘分布 αA和 αT均大于较不稳定的A03 机 组 ；A09 机 组 的 Pstable远 大 于 A03 机 组 的Pstable，这直接反映了A09 机组的风向稳定性较A03 机组好。

从风电机组风资源数据中计算抽取的参数集 αA，αT和 Pstable可直接反映风电机组的风向波动特性。 αA，αT和 Pstable越大，则该风电机组风向的稳定性越好，实现了风向波动特性的精确量化描述。

5 偏航系统参数优化初步研究

在Matlab 软件中建立本文研究的偏航控制器仿真模型。 采用 2018 年3 月 1 日至 8 日的 1 s采样风速和风向数据作为偏航控制器仿真模型输入。 两台机组的初始偏航参数偏航误差阈值和偏航误差持续时间阈值分别为15°和30 s。 为研究不同偏航参数下机组的发电量和偏航次数，并简化研究过程，将每台机组的偏航误差阈值以2°为步距，范围为[9°，21°]，偏航误差持续时间阈值以2 s 为步距，范围为[20 s，40 s]，并将两个参数互相组合，共形成7×11=77 种偏航参数组合分别作为两台机组的偏航控制参数。 以两台机组各自的风资源数据作为模型输入进行仿真，计算得到不同偏航参数组合下的两台机组各自的发电量和偏航次数。 选取两台机组各自具有代表性的偏航系统参数进行优化（表5）。

表5 A03 机组和A09 机组仿真优化前后结果Table 5 Comparison of results for A03 and A09

对于风向稳定性较差的A03 机组，将两个偏航参数适当增大，降低对波动频繁风向的敏感性，同时节省了偏航电机的自耗电，减少了偏航系统疲劳载荷。 对于风向稳定性好的A09 机组，将两个偏航参数适当减小，增加对稳定变化风向的灵敏度，发电量显著增加。

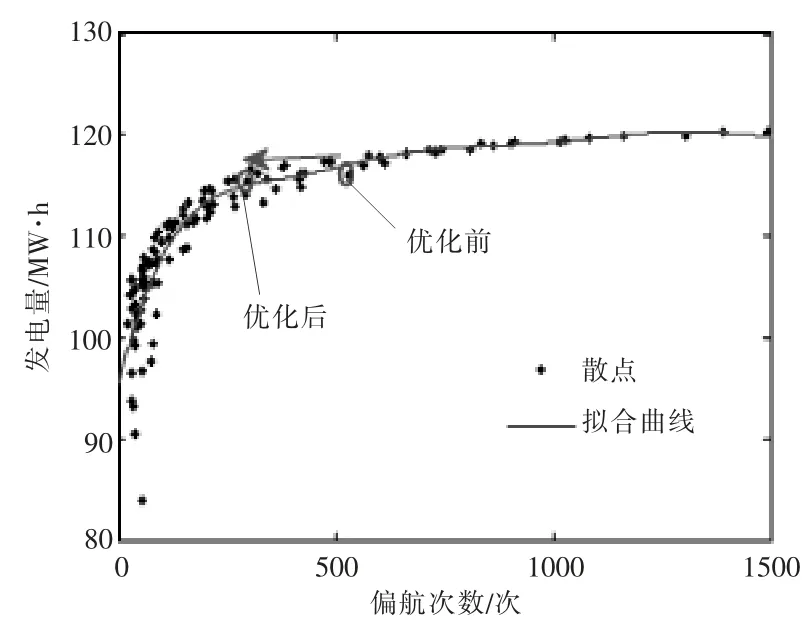
图8 A03 发电量的变化趋势Fig.8 Power generation trend of A03

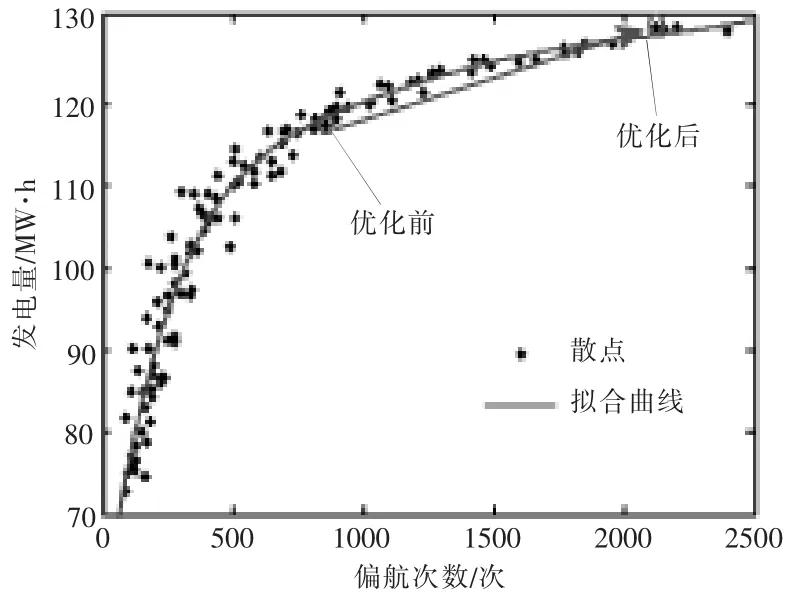
图9 A09 发电量的变化趋势Fig.9 Power generation trend of A09

图8 和图9 分别为 A03 和 A09 机组在不同偏航参数组合下仿真得到的发电量-偏航次数散点图。 随着偏航次数的增加，A03 和A09 机组的发电量均先迅速增加，后增幅减缓。 对于A03 机组类型，当偏航次数达到某个拐点时 （约为300次），发电量的增幅会大幅减小，在拐点之后，即使增加偏航次数，发电量增幅呈平缓趋势。A09 机组类型不存在明显的拐点，尽管发电量的增速为先快后慢，但增幅依旧较大。

6 结论

本文通过风电机组风资源数据，采用概率统计方法对风向波动特性进行了研究，得到以下结论。

①针对目前缺乏风向波动衡量指标的问题，提出了基于风电机组本地风资源数据的风向波动幅值-波动持续时间的二维风向波动量细化描述方法。

②采用Weibull 分布拟合风向波动的边缘分布概率，以Frank-Copula 函数作为连接函数，构建了二维风向波动量的联合概率密度函数，与现场运行数据进行比对分析，验证了该风向联合概率密度函数对两台机组本地风向描述的正确性。

③提出了定量精确描述风电机组本地风向波动特性的一组概率分布指标集 αA，αT和 Pstable。 通过采集风电机组较长时段的秒级风资源数据，利用本文方法可计算得到描述本地风向波动性的上述量化指标。

④初步研究了不同风向波动特性机组的偏航系统参数优化效果，并进行了对比。