基于深度学习的齿轮箱故障模糊诊断方法
牛 冲 ,王灵梅,陈立明,孟恩隆
(1.山西大学 山西省风电机组监测与诊断工程技术研究中心,山西 太原 030013; 2.阿尔斯特大学,贝尔法斯特 BT370QB)
0 引言
齿轮箱作为风电机组传动系统重要组成部分,故障往往在低速、大负载和闭环的条件下发生,由于其振动信号的非线性、非平稳性,给故障诊断带来不小挑战[1],[2]。 随着人工智能技术的发展,为各个行业提供了新的技术手段,深度学习作为机器学习的一种,在图像识别、计算机视觉等领域取得发展,目前在电力、航空等领域也有了一些应用[3],[4]。
针对齿轮箱故障诊断的研究主要有小波变换、包络谱分析、经验模态分解(EMD)、集合经验模态分解(EEMD)、神经网络等[5],[6]。 这些研究主要存在的问题是故障特征需要人工提取,导致其诊断精度受数据样本影响,而且在大数据背景下对海量数据处理能力有限。 深度学习作为人工智能代表的技术之一,它很好地解决了浅层神经网络非线性性能较低的问题,并且具有良好的泛化能力。 正是由于深度学习在自动提取特征与模式识别方面的独特优势与潜力,为解决复杂系统故障诊断的研究提供了新的研究思路[7]~[9]。将传统的诊断方法与深度学习相结合成为研究的热点,相关研究已经取得了一些进展。 文献[10]将稀疏自编码算法应用到频谱包络曲线,在提高诊断效果的同时,降低了计算的复杂度。 文献[11]利用深度学习来提取时频特征组成的联合特征向量,从而实现对不同故障识别。
本文构建一维卷积神经网络故障特征提取模型。 通过多层感知器对故障特征进行提取、重构,以达到对故障信号的有效表征,提高故障识别的准确率,并将模糊集合理论应用于多分类器中。以平均隶属度作为判断故障程度的标准,提高了故障诊断的精度,并在实验中验证了本方法的有效性。
1 卷积神经网络
1.1 基本结构
卷积神经网络是一种模仿大脑视觉皮质进行图像识别和处理的深度网络。主要由输入层、卷积层、池化层、全连接层和输出层组成。 可以通过增加卷积层和池化层得到更深层次的网络结构,其全连接层同样也可以采用多层机构。在卷积神经网络结构中,大多通过池化层和卷积层交替的堆叠来构成基本的拓扑结构,卷积层实现对上层输入数据空间特征的提取,并通过池化层对其进行降维压缩。 无论卷积层还是池化层其实质都是可以用于提取输入数据特征的滤波器,通过这些滤波器对输入数据进行逐层提取以获得数据中的特征,并把提取的特征更抽象化,最终实现对原始数据的压缩、平移和旋转操作后特征表示的不变性。
1.2 卷积神经网络训练方法
和多数神经网络一样,卷积神经网络中的参数训练使用误差反向传播算法。 本文以4×4 的输入图为例,着重介绍卷积层和池化层的误差反向传播,在反向误差计算中,卷积层改写为全连接层,池化层改写为部分连接的全连接层。
1.2.1 卷积层误差传播
图1 所示为将卷积层改写成全连接形式,对输入数据进行卷积操作,经过激活函数得到特征映射图。卷积核的权重调整和多层神经网络相同,从最上层的连接权重进行逐层调整,并使用交叉熵代价函数作为误差函数。
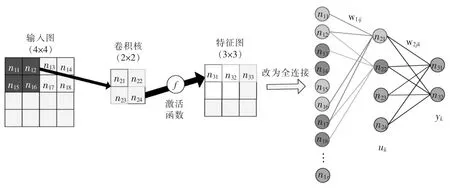
图1 卷积层的误差传播Fig.1 Error propagation of the convolutional layer
卷积核的权重调整和多层神经网络一样,从上层的连接权重逐层进行调整,图1 中上层权重调整为
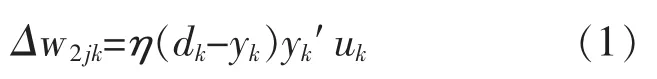
根据上层的链式法则,对单一单元的连接权重的调整,即:
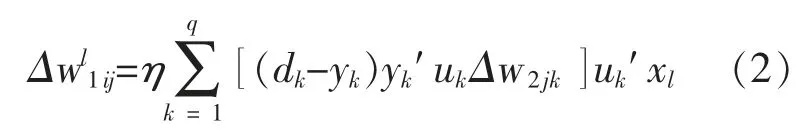
累积所有单元的连接权重调整值,得到最终的调整值。
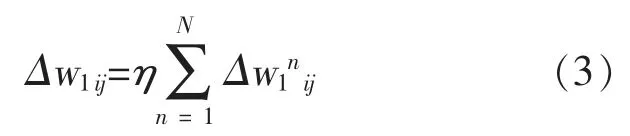
式中:η为学习率;d 为理想输出;y 为实际输出。
1.2.2 池化层误差传播
先将池化层改为部分连接的全连接层,每个池化区域内的单元分别与其池化后得到的单元相连,这样就可以把池化层看作是部分连接的全连接层(图2)。 由于本文采用平均池化,因此,误差在与之相连的每个单元之间传播,且每个连接权重均须调整。
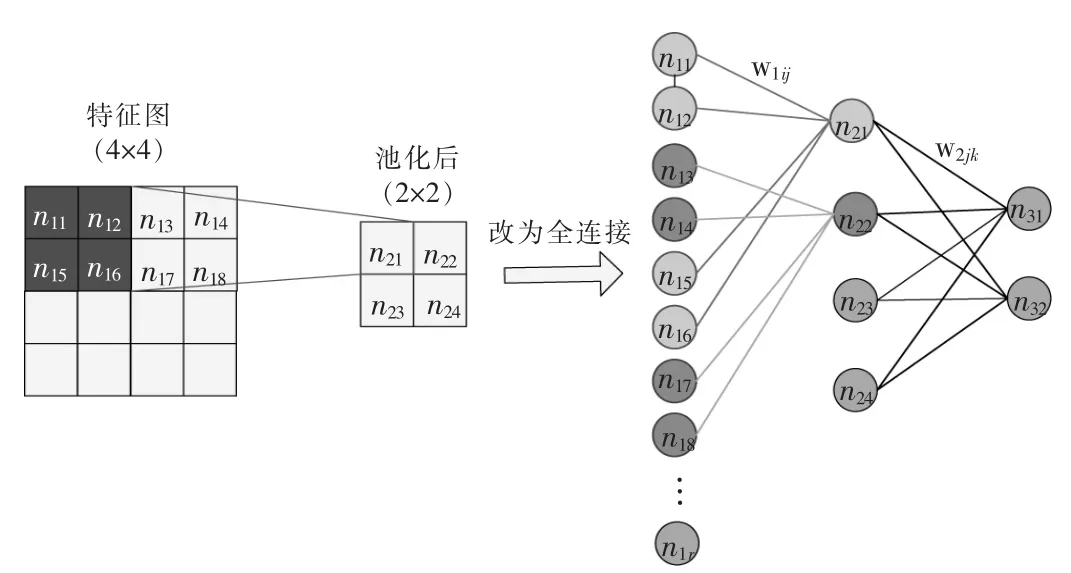
图2 池化层的误差传播Fig.2 Error propagation of the pooling layer
1.3 自适应学习率(AdaDelta)算法
超参数是困扰神经网络训练的问题之一。 超参数主要包括学习率、网络层数、权值初始化、单层网络神经元数和正则惩罚项(惩罚函数)。 这些参数不可以通过常规学习获得,最初只能通过人工不断实验。 随着深度学习对超参数优化的研究开始增多,自适应调整学习率方面的研究也开始增多,本文采用Matthew D Zeiler 提出的AdaDelta算法。 其算法流程如下:
步骤 1:设置固定值: ρ=0.95;ε=1e-8
步骤2:初始化变量:
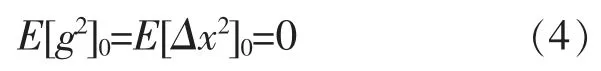
步骤3:设置循环次数T
步骤4:计算梯度:
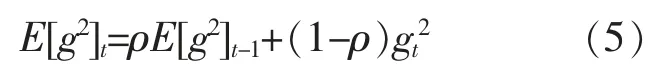
步骤5:计算更新:
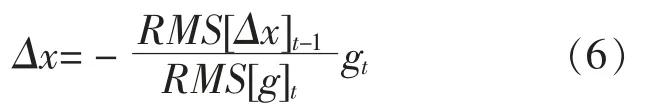
步骤6:累积更新:
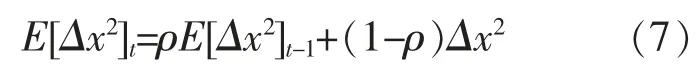
步骤7:更新学习率:

步骤8:达到训练次数自动结束。
式中:x 为学习率,且初始值为 0;ρ 为衰减率;ε 为常值;RMS 为梯度的均方根。
2 模糊多分类器设计
2.1 多分类器Softmax
风电机组齿轮的常见状态包括正常、磨损、点蚀和断齿。决定对其故障诊断属于多分类问题,本文使用多分类器Softmax 对其进行有效分类。 不同于以伯努利分布为模型建模的Logistic 分类器,Softmax 分类器是以多项式分布为模型建模,它可以分多种互斥的类别。
假设训练样本集合 X={x1,x2,...,xN},其对应的样本属于类别 C={1,2,...,k}中的唯一一种,则p(y=k|xi)表示 xi属于 k 类别的概率。
作如下定义:
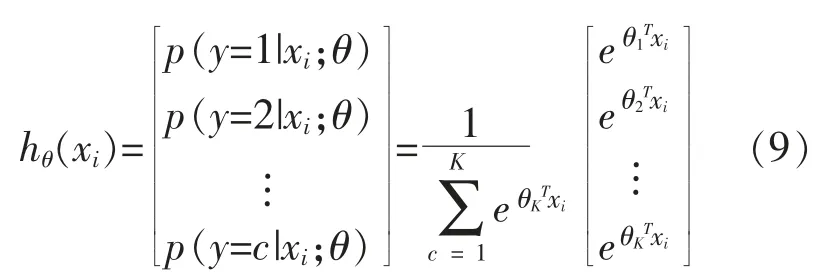
式中:θ=[θ1,θ2,…,θk]T为 Softmax 回归模型的训练参数,其列元素之和为1,即所有类别发生概率和为1。
该模型的代价函数为
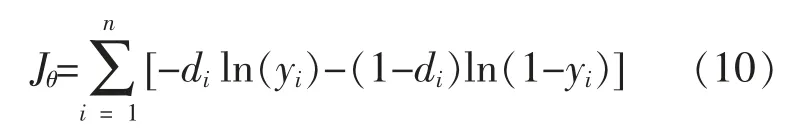
式中:yi为输出节点的输出;di为来自训练样本的正确输出;n 为输出节点的个数。
利用拟牛顿法求得最优参数。
2.2 模糊集合与隶属度函数
1965 年,美国控制论专家Zadeh 教授创立了模糊理论,经过50 多年的发展,模糊理论在工程领域取得了广泛应用。 由于对故障程度分级属于一个模糊命题,因此,本文利用模糊理论具有的较强的结构性知识表达能力,将其应用于多分类器,增强了分类的表达能力。
设U 为论域,模糊集合A∈U,x 为样本点振动幅值,μx为隶属度函数值。通过对前期采集数据的模糊统计得其隶属度值分布情况,并由线性拟合得其隶属度函数。
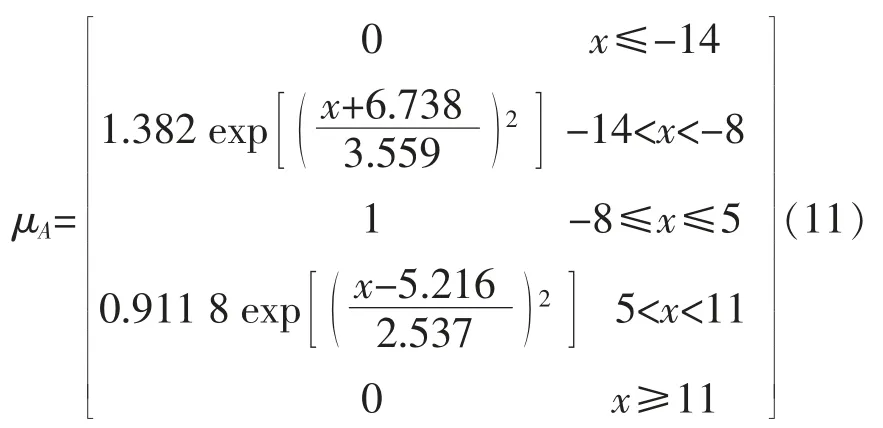
设每个样本点个数为n,则故障程度判别规则中的平均隶属度为
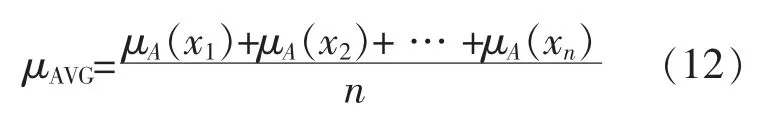
设模糊集合 X={X1,X2,X3,X4} ,Xi为第 i 种状态对应的平均隶属度。 多分类器中的分类集合为清晰集 Y=(Y1,Y2,Y3,Y4),其中 Y1=[1 0 0 0]T,Y2=[0,1,0,0]T,Y3=[0,0,1,0]T,Y4=[0,0,0,1]T。 Z是X 与Y 的一个模糊关系并由其表示推理,则由推理的合成规则得:
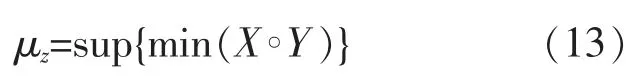
由经验给出故障程度判定规则(表1)。

表1 故障程度判定规则Table 1 Failure degree determination rule
3 模型构建与训练
本文构建了基于卷积神经网络的故障特征提取模型和由模糊多分类器构成的模糊识别模型 (图3)。 卷积神经网络模型主要由两个卷积层、两个池化层和一个全连接层组成;故障识别模型是通过在Softmax 分类器中加入模糊隶属度函数对提取的特征进行识别,以此来增加故障分类精度。

图3 基于卷积神经网络的模糊诊断模型Fig.3 Fuzzy diagnosis model based on convolutional neural network
由图3 可知:在特征提取过程中,对原始输入进行两次卷积池化后,提取到更抽象、更深层的特征并通过全连接层得到完整的特征表征;在特征识别中,模糊多分类器在对特征属性进行识别的同时,完成对状态更精细的辨识。
图4 为网络模型训练流程图。 在整个训练过程中,通过调整网络层数、卷积核个数、激励函数种类等得到最终的模型参数,将自适应学习率算法与传统训练方法进行比较,在结果分析部分给出结论。
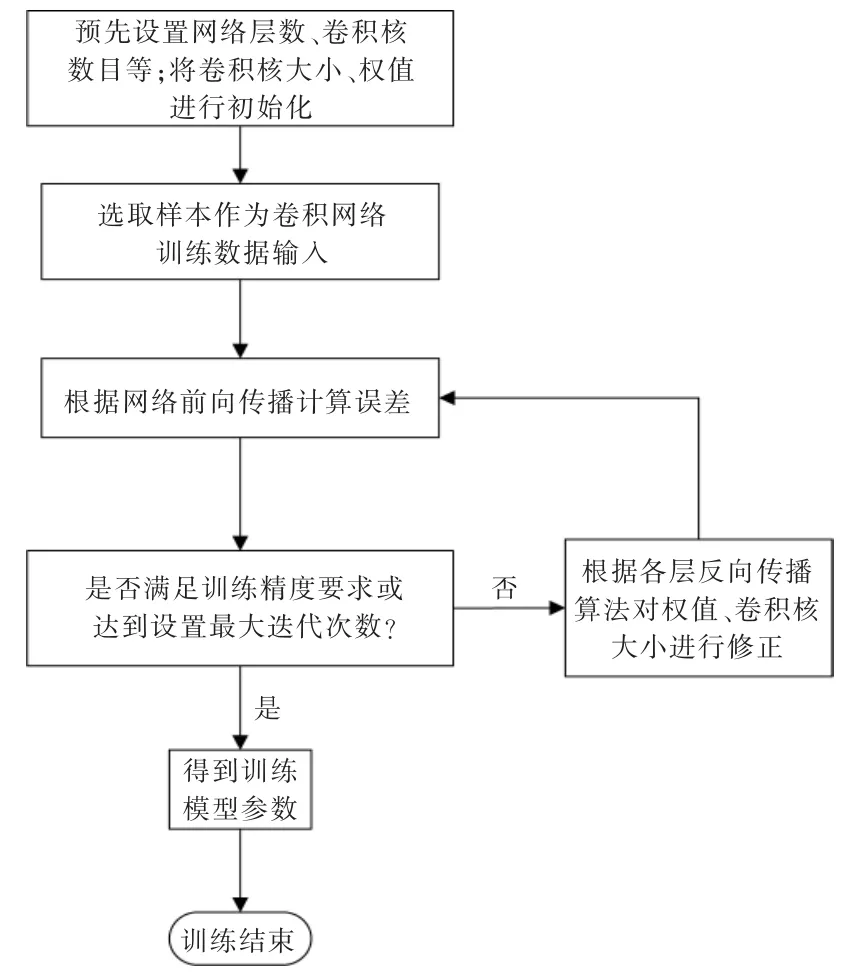
图4 网络模型训练流程Fig.4 Network model training process
4 实验结果分析
4.1 实验平台介绍
本文使用自主研发的风电机组传动系统故障模拟实验平台采集的数据进行结论验证。 实验平台主要由变频控制器、传动系统故障模拟试验台、采集仪、采集软件等组成。变频控制器通过调节频率进而控制转速,其高速端转速可达1 500 r/min;信号采集使用某国产品牌的24 位采集仪,其采样频率最高为512 kHz,能满足实验要求。
通过对输出端施加机械作用力来模拟实际情况下的负载变化,设置的故障点为齿轮箱三级增速端,对齿轮4 种状态,即正常、磨损、点蚀、断齿进行数据采集(图5)。

图5 齿轮4 种不同状态Fig.5 Gears in four different states
4.2 实验结果
根据双馈式风电机组转速转矩的特点,设定两种工况:第一种工况高速端输出转速为1 000 r/min,低速侧输入转速为14.40 r/min(转速比69.48∶1); 第二种工况高速端输出转速为500 r/min,低速侧输入转速为7.20 r/min。 采样频率为10.24 kHz。 分别在两种工况下对齿轮不同状态的数据进行采集,不同状态的高速端齿轮数据采集250 组,共 2 000 组。
4.2.1 模型训练结果
图6 所示为4 种状态的初始信号及其经过卷积池化后得到的特征向量图。 由图6 可知,故障信号在经过卷积网络训练后,其故障特征更为明显。
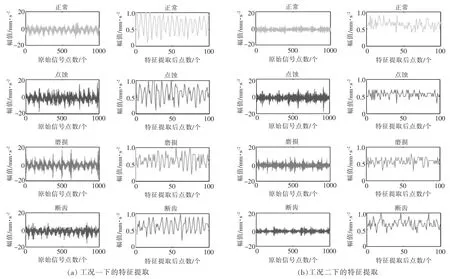
图6 特征向量提取图Fig.6 Feature vector extraction map
随着迭代次数的增加,训练准确率不断提高。重复进行10 次试验,结果显示平均训练分类准确率达到99.76%,平均测试准确率为98.25%,且在两种工况下准确率无显著差异,表明本方法对故障分类的效果明显达到了预期(图7)。
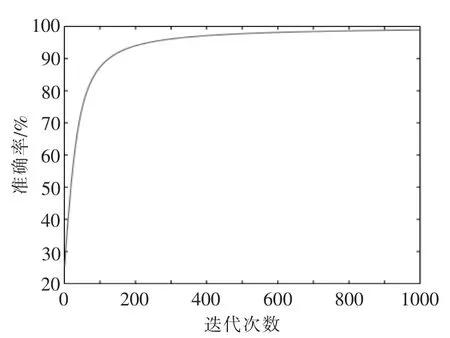
图7 训练准确率Fig.7 Training accuracy
本文还将随机梯度(SGD)与 AdaDelta 两种训练算法进行比较(图8)。 由图8 可知,在相同条件下,AdaDelta 算法比SGD 算法能更快地降低学习误差,即学习速率更快。
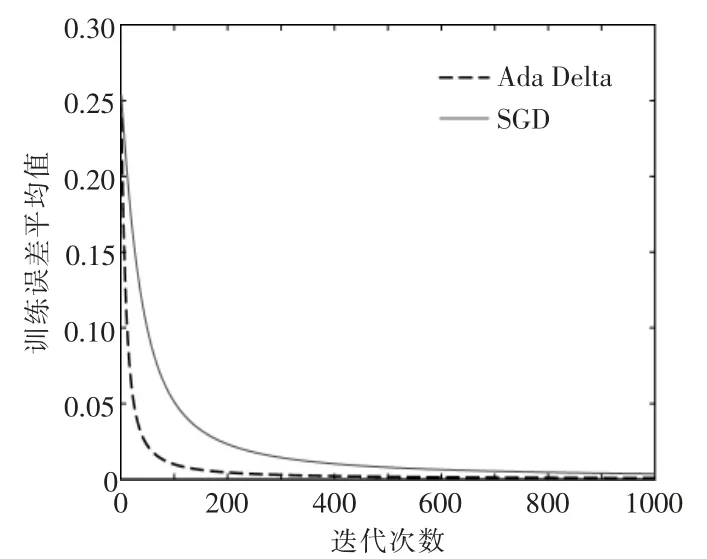
图8 两种学习算法对比Fig.8 Comparison of two learning algorithms
4.2.2 模糊分类结果
本文选取断齿状态下不同故障程度的数据进行验证,其中齿轮1 断齿程度较轻,齿轮2 断齿程度较重(图9)。 各采集100 个样本,以工况一为例,故障部分的样本结果如表2 所示。

图9 两种不同故障状态下的断齿Fig.9 Broken teeth in two different fault states
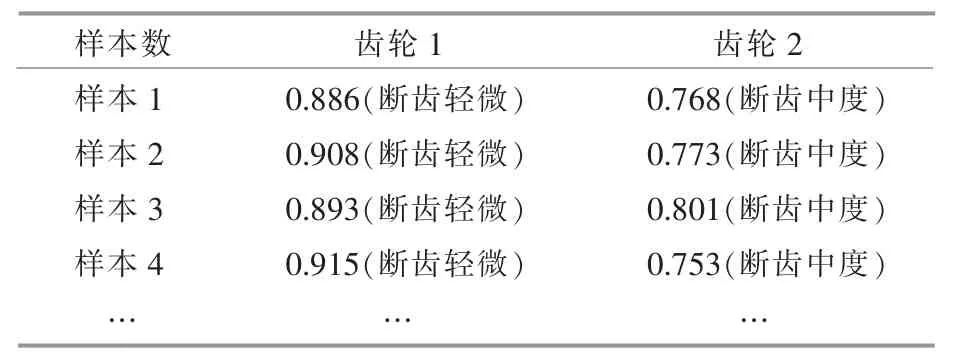
表2 不同故障状态下的断齿模糊分类Table 2 Fuzzy classification of broken teeth under different fault conditions
重复多次实验并统计结果,显示所有样本均能正确判断出故障类型为断齿,并且对故障程度的准确率最高可达90%,部分样本可能会在状态交叉处出现偏差。 重复之前步骤得到工况二的结果与上述结果无差异。 对于齿轮在同一故障状态下的不同故障程度,本方法能有效诊断,从而为风场运维提供技术支持。
5 总结
针对齿轮箱振动信号的非线性、 非平稳导致的传统时频分析方法对故障信号分解和故障特征向量提取能力的不足,通过构建一维卷积神经网络模型对不同状态下的特征向量进行有效提取,在训练中采用了自适应动量算法提升训练能力并与随机梯度下降法进行了对比。 通过数理统计方法找到模糊分类的隶属度函数,并由此确定了模糊分类的规则,提升了故障分类的精度。本文为齿轮箱故障诊断提供了一种有效方法,尤其是对故障程度的判定,为早期故障的预警提供了一种可行的方法。

