基于改进BPNN-SVR算法的土壤盐分参数与有机质相关性研究

王 正，孙兆军，禹 昭，何 俊，韩 磊，李 茜

(1.宁夏大学土木与水利工程学院，银川 750021；2.宁夏大学新华学院，银川 750021；3.宁夏大学环境工程研究院，银川 750021；4.宁夏(中阿)旱区资源评价与环境调控重点实验室，银川 750021)

0 引 言

土壤有机质是耕作土壤中最重要的属性之一，它不仅为作物的生长提供条件，而且在改良土壤理化性质方面发挥着重要作用，尤其在盐碱土壤生态修复中的表现更为显著[1]。大量研究表明，可利用多种工具进行土壤有机质含量的估算，如粒子群优化[2]、偏最小二乘回归[3]、高光谱数据处理[4]等。另外，土壤盐分参数与有机质含量之间存在极其复杂的联系，这使得利用智能算法来高效、准确估算有机质含量成为可能[4]。

利用智能算法来估算土壤有机质含量的方法，国内外学者做了大量工作[5,6]。刘二永[7]等研究了环境因子与有机质的相关关系，并利用环境因子所对应参数结合回归-光滑薄板样条插值方法(R-STPS)对有机质含量进行了空间预测，预测结果表明，R-STPS能高效地进行预测。但其建立的模型过于简单，未考虑土壤类型和耕作方式等对有机质的影响。蔡剑华[8]等探讨了将经验模态分解方法与近红外光谱数据结合来预测土壤有机质含量，结果表明，该方法具有较高的可靠性，预测效果明显优于传统方法。Razakamanarivo[9]等利用线性回归模型、多元回归模型和回归树三种方法结合生态环境因素和空间因素对土壤有机质含量进行了预测，结果表明回归树相比前两种方法来说具有更高的精度，同时也非常适合处理非线性的数学模型。Manpreet[10]等讨论了不同类型的土壤在不同含盐量的情况下对土壤有机质含量的影响。

目前，多数估算土壤有机质含量的文献都是基于高光谱、遥感数据等无人机遥感技术，再结合智能算法对其进行了预测与反演[11,12]。但是这些方法最大弊端是只能针对表层大约10 cm左右的土壤进行预测反演，无法应用于深层土壤，而且，由于土壤表层会被其他物质或植被掩盖和包围再加上电磁波的穿透能力有限，这样就难免会对预测的结果形成消极影响[13]。另外，无人机遥感很容易受气候、地理条件等客观因素的影响，会导致不充分、不可靠和不准确的计算结果[14]。鉴于BP神经网络(BPNN)变化多端的结构形式以及强大的非线性模型的表现能力，回归型支持向量机 (SVR)在多因子检测分类领域中是一种非常有效且精确度较高的工具[15-17]，它们被广泛应用于模式预测、识别等智能预测评估领域[18-20]。本研究针对BPNN学习速度慢且容易陷入局部最优值的缺点，对其网格中的权值和阈值进行了改进，而且基于改进BPNN优化算法的SVR提出有机质含量估算模型。分析土壤有机质含量与盐碱土盐分之间的相关关系，并利用盐分参数对宁夏吴忠树新林场的盐碱土壤有机质含量进行预测，并从估算结果、决定系数、均方误差等方面进行对比分析。

1 材料与方法

1.1 研究区概况

树新林场地处宁夏平原中部的青铜峡市(38°36′N，105°56′E)，位于黄河西岸，属中温带半干旱气候，昼夜温差大，年平均气温为8.5 ℃，年降水量为260.7 mm。树新林场处于黄河冲积平原，土壤主要以砂质壤土为主，次生盐渍化较严重，其中原状土饱和泥浆电导率介于4.60～25.50 dS/m之间，pH值介于8.50～11.80之间。

土壤盐分数据采集于2017年8月。此次选取了吴忠树新林场内的盐碱试验地，将样地设置面积为16 m2的等大正方形区域11个，然后在正方形形心位置处重复取3次样，采样深度为0～20、20～40、40～60、60～80和80～100 cm等5个处理，共采集样品165个。采集的土壤样品带回后，经过挑拣杂物、自然晾干、过1 mm孔筛等前处理工序后，然后按照土壤盐分、土壤有机质、土壤pH值等项目逐步进行测量，求取平均值后的结果如表1所示。

1.2 研究方法

建立基于改进BPNN与回归支持向量机(SVR)的有机质预测模型。其中，利用改进BPNN方法选取最优SVR参数，而SVR则选用分块算法对样本数据进行训练，减少算法的运算时间，同时研究不同核函数对模型性能的影响，并将土壤盐分参数作为预测变量并进行回归分析。

1.2.1 回归支持向量机(SVR)

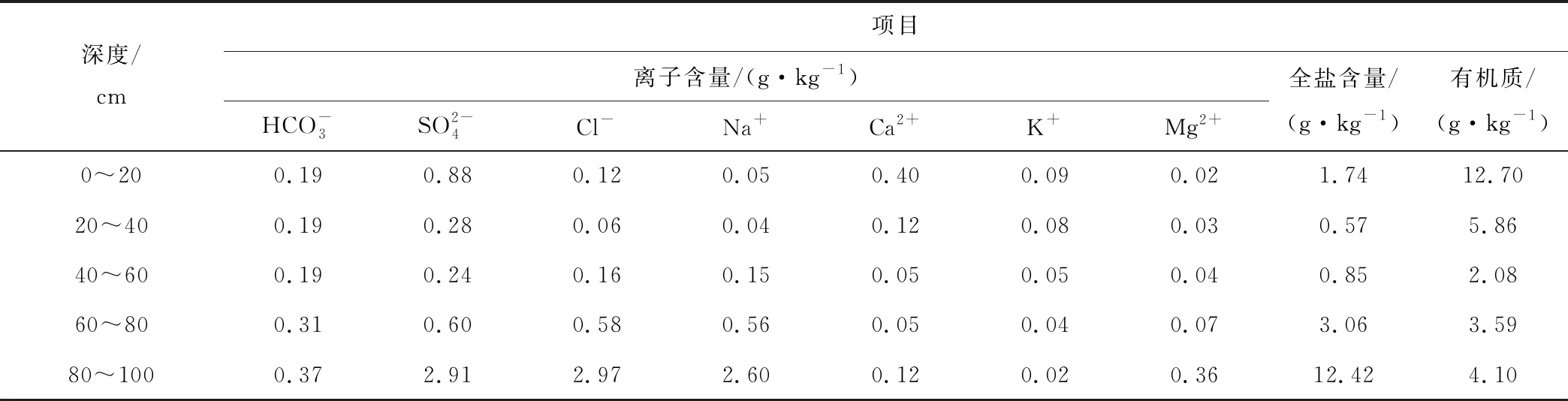
表1 试验区中的土样数据Tab.1 Soil sample’s data in the test area

建立如下的线性回归函数：

f(x)=λΨ(x)+ξ

(1)

式中：λ为权重参数向量；Ψ(x)为非线性映射函数；ξ为偏置参数向量。

为了便于处理，可以利用Largrange函数将原问题转换为对偶问题，最终得到回归函数为：

f(x)=λ*Ψ(x)+ξ*=

(2)

式中：xi为待求解问题中的支持向量。

1.2.2 BP神经网络(BPNN)

误差反向传播算法(EBPA)是著名的BPNN学习算法，由Rumelhart[21]等人提出。中心思想是将实际输出与理想输出之间的误差归因于权值和阈值的“过错”，通过反向传播将该误差“摊派”给各个神经元，并对权值和阈值进行调整。

因此，本文利用式(3)和式(4)对权值和阈值进行调整改进了算法。

(3)

(4)

式中：η1和η2分别为隐含层和输出层的学习步长。

1.2.3 模型评价

为了更好地研究预测模型的精度，本研究利用决定系数(R2)来衡量其稳定性，用均方差(MSE)来反映模型的预测能力，用平均相对误差(ARE)反映预测模型的可信程度，评价指标的误差值越小就说明模型的精度越高。

2 结果与分析

2.1 相关性分析

2.1.1 描述性统计分析

剔除异常数值后的土壤有机质统计特征如表2所示。从表2可以看出，变异系数为63.46%，所以树新林场的土壤有机质属于中等变异。检验土壤有机质数据的偏度和峰度，偏度为0.34，峰度为-0.71，基本服从正态分布。

2.1.2 土壤有机质与土壤盐分参数相关性分析

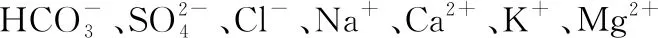
表2 树新林场的土壤有机质统计特征 Tab.2 Statistic characteristic values of soil organic matter in Shuxin forest farm

表3 土壤有机质与土壤盐分参数间的相关系数 Tab.3 Correlations between soil salinity parameters and soil organic matters

2.2 回归模型的建立

基于改进BPNN算法的SVR参数寻优的具体步骤如下：①随机确定初始的层间神经元的权值和阈值，以及其他参数的初始化。②根据选定的神经网络模式计算输入层、隐含层和输出层等三层的输入和输出。③按照式(3)和式(4)修正权值和阈值。④计算全局误差，判断误差是否满足要求，满足时停止运算，否则返回第②步后反复训练直到男足要求。

本研究中模型运算时由MATLAB编程实现，改进BPNN-SVR模型的具体运算流程如图1所示。

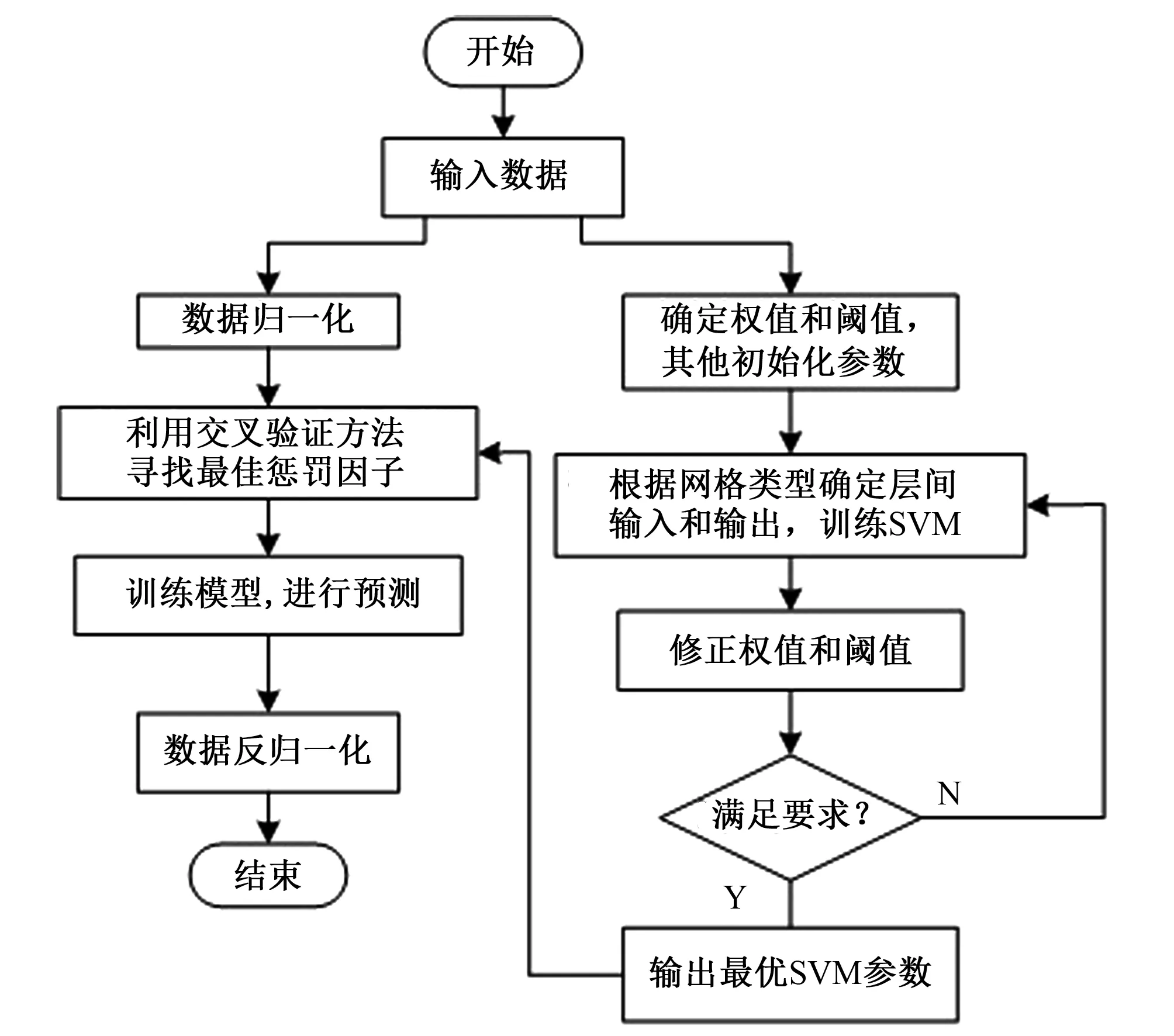
图1 改进BPNN-SVR模型建立流程图Fig.1 The flowchart of the improved BPNN-SVR model

2.3 预测过程

本研究共采集了165个土样的盐分参数和有机质含量数据，为了不失一般性，采用随机产生训练集和测试集的方法，即随机选取120个样本作为训练集，剩余45个样本作为测试集对模型进行性能评价。本研究是基于改进BPNN-SVR建立的模型进行土壤有机质含量估算，而在SVR中，选取核函数的类型和确定最优核函数参数是最为关键的步骤之一，主要的核函数类型有线性、多项式、RBF和多层感知机等。其中，线性核函数无任何其他参数；多项式核函数需要选取阶数d，这里选取d=3；RBF核函数和多层感知机核函数需要选取惩罚因子c、方差g和不敏感损失参数ε，这里利用5-折交叉验证方法(5-folder cross-validation，k-CV)结合网格搜索法寻找最佳参数c、g和ε，其搜索范围分别为[0,100]、[0,100]和[-10,10]，并在MATLAB软件中进行了多次迭代试验，最终得到核函数最优参数。

得到了核函数最优参数如表4所示，以RBF核函数为例进行了模拟研究，由于训练集和测试集是随机产生的，因此每次运行的结果均不相同，在多次次运行结束后求取平均值后，结果如图2、图3所示。

表4 不同核函数的最优参数 Tab.4 Best values for different parameters of kernel

2.4 对比分析

现利用评价指标来评价图2和图3中的预测结果。其中，训练集的吻合度较高，决定系数达到了0.938，均方误差为0.074 2，而测试集均方差为0.106 5，吻合度也较好，决定系数达0.941 5，这表明基于改进BPNN-SVR的土壤有机质估算模型具有非常好的泛化能力。为了对比改进BPNN-SVR模型的性能，这里将之与传统的BPNN网络模型进行对比并采用相同的训练集和测试集，其测试集的预测结果如图4所示。这种情况下，传统的BPNN模型的决定系数为0.870 3，均方差为0.116 2，相对于改进BPNN-SVR模型比较不难发现，传统的BPNN模型的性能要劣于改进BPNN-SVR模型的性能。

本研究选用的核函数为RBF核函数，为了讨论不同核函数对模型训练集合测试集的影响，以下进行20次模拟研究后求取平均值的对比结果，如表5所示。

据表5中有机质含量的实际数据和不同核函数预测模型的预测结果及分析可知，以测试集结果为例，传统的BPNN模型预测结果的平均相对误差(9.78%)高于改进BPNN-SVR模型，而且决定系数(0.804 9)低于多项式核函数模型(0.849 8)和RBF核函数模型(0.890 8)。总体上说，传统BPNN预测模型在性能指标上要劣于改进BPNN-SVR预测模型，而且设计结构和确定参数要相对困难。另外，虽然多项式回归模型预测结果的决定系数达0.849 8，但是平均相对误差(7.55%)和均方差(0.147 6)明显高于其他核函数模型，说明多项式核函数模型的泛化能力较差。对于改进BPNN-SVR模型来说，不同核函数对模型预测结果的影响存在显著差异。多项式核函数模型预测结果中的相对误差、均方误差均大于RBF核函数模型的预测结果，线性核函数模型的预测结果中决定系数最小，均方误差较大，不适合用于土壤有机质含量的估算。多层感知机核函数模型的预测结果平均相对误差和局方误差较低，性能仅次于RBF核函数模型。RBF核函数模型预测结果平均相对误差(5.98%)和均方误差(0.074 6)均小于其他模型，决定系数也高达0.890 8，与此同时，基于RBF核函数的改进的BPNN-SVR模型相对于传统的BPNN模型来说，训练集预测结果中的平均相对误差和均方差降低了42.22%和34.21%，决定系数提高了11.32%；测试集预测结果中的平均相对误差和均方差降低了38.85%和30.99%，决定系数提高了10.67%。通过与其他模型进行比较得知，基于RBF核函数的改进BPNN-SVR模型具有明显的优势，且预测精度最高，非常适合于土壤有机质的估算。

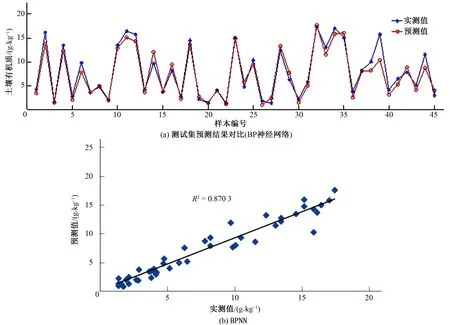
图4 传统的BPNN模型预测结果对比Fig.4 Comparison between forecasted values with actual values of conventional BPNN model

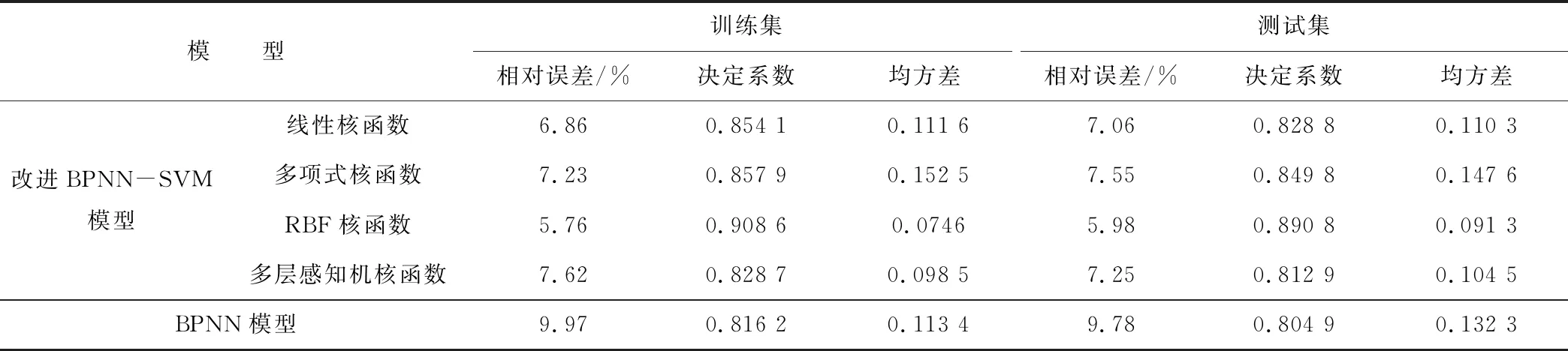
表5 不同模型预测结果的对比Tab.5 Comparison of the prediction results for different models

3 结 语

(1)通过对已检测165个土样的盐分参数和有机质含量进行相关性分析，得到土壤盐分离子含量、全盐含量与土壤有机质呈强相关性，其中HCO- 3的相关系数最高，达到了0.559 8，利用改进BPNN来优化SVR的参数进行了土壤有机质的估算，并对预测结果进行了分析。

(2)将最优核函数参数应用到改进BPNN-SVR模型中并结合归一化后土壤盐分参数对土壤有机质含量进行估算的研究中，基于RBF核函数的模型在训练集和预测集中的表现优异，训练集中决定系数达到0.938，均方差为0.074 2，测试集中决定系数为0.941 5，均方差为0.106 5。在相同试验样本的情形下，利用传统的BPNN模型对土壤有机质也进行了估算，结果显示传统BPNN模型的性能略逊于本研究提出的改进BPNN-SVR模型。

(3)通过对比不同核函数条件下改进BPNN-SVR模型的预测结果发现，RBF核函数的预测结果能够较为理想地估算土壤有机质的含量，且可信度较高，平均决定系数为0.908 6，平均均方差为0.074 6，平均相对误差为5.6%。