基于主成分分析和粒子群算法优化支持向量机的冻融土壤蒸发预报模型

解 雪，陈军锋，郑秀清，薛 静，翟小艳，杜鑫钰，魏一钊

(太原理工大学水利科学与工程学院，太原 030024)

0 引 言

中国季节性冻土区大多属于干旱半干旱地区[1,2]，干旱少雨、蒸发强烈加剧了该地区的水资源短缺情势。土壤蒸发作为土壤水分消耗的主要途径，并没有直接参与作物生长，属无效水分损失[3,4]。随着水资源短缺的加剧，季节性冻融地区的土壤蒸发已引起人们的重视，研究季节性冻融地区的土壤蒸发及其影响因素，准确估算冻融土壤蒸发量对提高干旱半干旱地区水分利用效率具有重要意义。

Feng等[5]采用自制微型蒸发器，通过冻融期大田实测数据研究了不同粒径砂层覆盖下的土壤蒸发规律，揭示了地表覆砂对土壤蒸发的影响。由于冻融期土壤蒸发量相对较小，且土壤蒸发量的测定易受暴风、低温寒冷等恶劣天气干扰，蒸发量的连续测定较为困难[6]，所以学者们多采用模拟研究的方法对冻融期的土壤蒸发进行研究。李瑞平[7]等基于SHAW模型研究了秋浇定额、秋浇时间对冻融期土壤累积蒸发量的影响；雷志栋[8]等基于SHAW模型模拟分析了地下水位埋深、负积温对冻结期潜水蒸发量的影响；陈军锋[9]等基于SHAW模型模拟了不同潜水位埋深下的土壤蒸发规律，揭示了不同潜水位埋深和土壤质地对土壤蒸发的影响。目前对冻融土壤蒸发的机理进行了大量研究，揭示了影响冻融土壤蒸发的因素，然而较为准确的预报冻融土壤蒸发量仍有一定的困难。

近年来，人工智能方法快速发展，具有能很好地解决小样本、非线性，高纬度和局部最小值问题[10]特点的支持向量机被广泛应用于水文预报[11-13]，地下水水质监测[14,15]，地下水水位预报[16]，土壤水力学参数预测[17]。但支持向量机的预测性能依赖于惩罚参数和核参数的选取，而粒子群算法是一种运算速度快，局部搜索能力强，求解精度高[18,19]的寻优算法，适合于支持向量机模型的参数优化。在季节性冻融期，影响土壤蒸发的因素复杂，耦合性强，会使得预测冻融土壤蒸发量的支持向量机模型过于复杂，降低预测准确率。此外，主成分分析能有效地提取数据的非线性特征信息，简化数据量，并保证原始数据的完整性。因此，本文采用主成分分析提取冻融土壤蒸发量影响因素的主成分，采用冻融期大田土壤蒸发实测数据和气象站监测资料，建立基于粒子群算法优化支持向量机的模型，进行冻融土壤蒸发预报。

1 材料与方法

1.1 研究区概况及数据的来源

1.1.1 研究区概况

研究区位于山西省水文水资源勘测局太谷均衡试验站。该试验站位于山西中部，晋中盆地南部，地理位置为112°30′E、37°26′N。试验区海拔高度777 m。属暖温带大陆性干旱与半干旱气候，春季风大雨少，冬季寒冷少雪。多年平均气温9.9 ℃，多年平均降水量415.2 mm，且主要集中在6-9月份。历史上最大冻土深度92 cm。多年平均相对湿度74%。多年平均风速为0.9 m/s[20]。

1.1.2 测定项目

田间试验于2017年11月至2018年3月在山西省太谷均衡试验站进行。冻融土壤蒸发量采用微型蒸发器测定，地表土壤含水率采用烘干称重的方法测定。地表土壤温度采用预埋式热敏电阻进行监测，监测时间与地表土壤含水率，土壤蒸发量同步，均为7 d/次(8∶00-9∶00 am)，冻融期间共监测17次。气温、相对湿度、风速。气压均由地面气象观测站自动监测，监测时间为每天8∶00,14∶00和20∶00。

1.1.3 样本数据集的构建

根据2017年11月至2018年3月监测的太阳辐射(x1)，日平均气温(x2)，地表土壤温度(x3)，地表土壤含水率(x4)，风速(x5)，气压(x6)，相对湿度(x7)，降水量(x8)，水面蒸发量(x9)和实测的冻融土壤蒸发量构成本文的样本数据集。由于土壤蒸发量，地表土壤温度和地表土壤含水率的样本数据以周为单位监测，样本数量较少，因此采用线性内插法生成123组以日为单位的样本数据，见表1。

1.2 研究方法

由于季节性冻融期土壤水分的相变及其与温度的强烈耦合作用，使得其影响因素颇为复杂。结合实测资料，本文分析的冻融土壤蒸发影响因素主要包括太阳辐射(x1)，日平均气温(x2)，地表土壤温度(x3)，地表土壤含水率(x4)，风速(x5)，气压(x6)，相对湿度(x7)，降水量(x8)，水面蒸发量(x9)等。若使用多个影响因素作为输入变量进行粒子群算法优化后的支持向量机建模，会提高模型的复杂度，从而使得计算量多且冗余的信息也较多。而主成分之间是相互独立的，由主成分组成的输入空间不存在自相关性[21]，因而有效地简化了建模时的复杂度，提高了模拟精度。

表1 冻融土壤蒸发样本数据Tab.1 Sample data of freeze-thaw soil evaporation

1.2.1 主成分分析

主成分分析(Principle Component Analysis)PCA是将多个指标化为少数几个综合指标的统计分析方法，旨在利用降维的思想，将多个具有相关性的原始变量进行线性组合成互不相关的综合因子即主成分[21]，简化数据量的同时并保证原始数据的完整性。

主成分分析的基本操作步骤如下：设数据集有n个样本，m个变量。

(1)为消除量纲及数量级对分析结果的影响，首先将原始变量数据进行标准化处理：

(1)

(2)

(3)

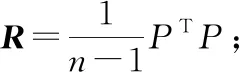
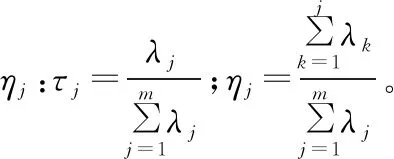
(4)计算主成分值Fj：Fj=Puj。

通过主成分分析，选取累积贡献率大于85%前k个主成分，并将前k个主成分代替原始数据进行分析和建模。

1.2.2 粒子群优化算法

粒子群算法(Particle Swarm Optimization) PSO是一种基于群体智能与适应度的全局优化算法，其基本特点是一种针对种群的并行搜索策略[22,23]。此算法中初始状态为一群粒子，每一个粒子向量代表一个SVM模型，该模型对应不同的C和g，即每一个粒子代表一个潜在最优解。粒子的特性包括位置，速度和适应值。粒子在寻优解的运动时，通过跟踪个体极值和群体极值更新自己的位置，相应的适应度值也随粒子的位置更新而更新。粒子的速度和位置更新公式为：

(4)

(5)

1.2.3 支持向量机

支持向量机SVM是由Vapnik V等人根据统计学理论提出的一种新的通用的学习方法，并且起初SVM是为了研究线性可分的问题提出的[24-26]。随着回归预测问题的引入，Vapnik等人在SVM分类的基础上引入了不敏感的损失函数，从而得到了具有较好性能和效果的回归型支持向量机[27]，根据有限的样本可以进行有效的回归预测。设给定训练样本集：{(xi,yi)|i=1,2,…,n}，n表示数据样本的个数。其中xi为输入变量的值：xi=xi1，xi2,…,xim；yi为对应的输出变量。

SVM的回归预测模型数学表达函数为：

(6)

exp(-g‖xi-xj‖2)g>0

(7)

式中：g为核参数。

(8)

式中：C为惩罚参数。

1.2.4 基于主成分分析和粒子群优化的支持向量机模型的构建

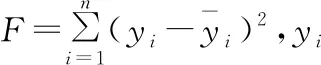
2 结果与分析

2.1 冻融土壤蒸发影响因素分析

季节性冻融期，太阳辐射、日平均气温和地表土壤温度是影响土壤冻融过程的主要因素，也是冻融土壤蒸发所需的重要热量来源。土壤冻结期，随着太阳辐射的逐渐降低，气温和地温随之下降，表层土壤形成冻层，地表土壤含水率降低，蒸发速率降低，蒸发量随之减少。水面蒸发量是表征冻融土壤蒸发外界条件的主要因素，水面蒸发量越大，表明当前的气象条件越利于蒸发。相对湿度是影响冻融土壤蒸发的另一重要因素，土壤冻结稳定阶段，密实的土壤冻层阻碍了地表土壤水分和深层土壤水的联系，气温较低且仅有少量的液态水分，地表土壤蒸发只能以水汽的形式进行[28]。在这种情况下，如果相对湿度越高，大气中的水汽含量越多，水汽就越接近饱和，从而增大空气中气压。地表附近相对湿度梯度和气压梯度越大，土壤蒸发便会越大。而风速能够加快地表土壤附近的空气流动，风速越大，空气交换越频繁，地表附近的饱和空气状况被削弱，从而促进土壤蒸发。降水量是增加冻融土壤蒸发的重要因素之一，降水量增加了土壤蒸发的水分来源，从而增大了土壤蒸发。

2.2 基于主成分分析和粒子群优化算法优化的支持向量机模型的应用

选择影响冻融土壤蒸发的9个主要因素，包括太阳辐射(x1)，日平均气温(x2)，地表土壤温度(x3)，地表土壤含水率(x4)，风速(x5)，气压(x6)，相对湿度(x7)，降水量(x8)和水面蒸发量(x9)代入 (1) 式进行数据的归一化处理，并将归一化处理后的结果输入SPSS软件进行主成分分析。

利用SPSS软件分析得到主成分对冻融土壤蒸发量影响因素的样本数据解释的特征值和累积方差贡献率(图1)。由图1可知，前3个主成分(F1, F2, F3)的累积贡献率高达86.27%，表明前3个主成分可以概括原始数据中9个变量的绝大部分信息。

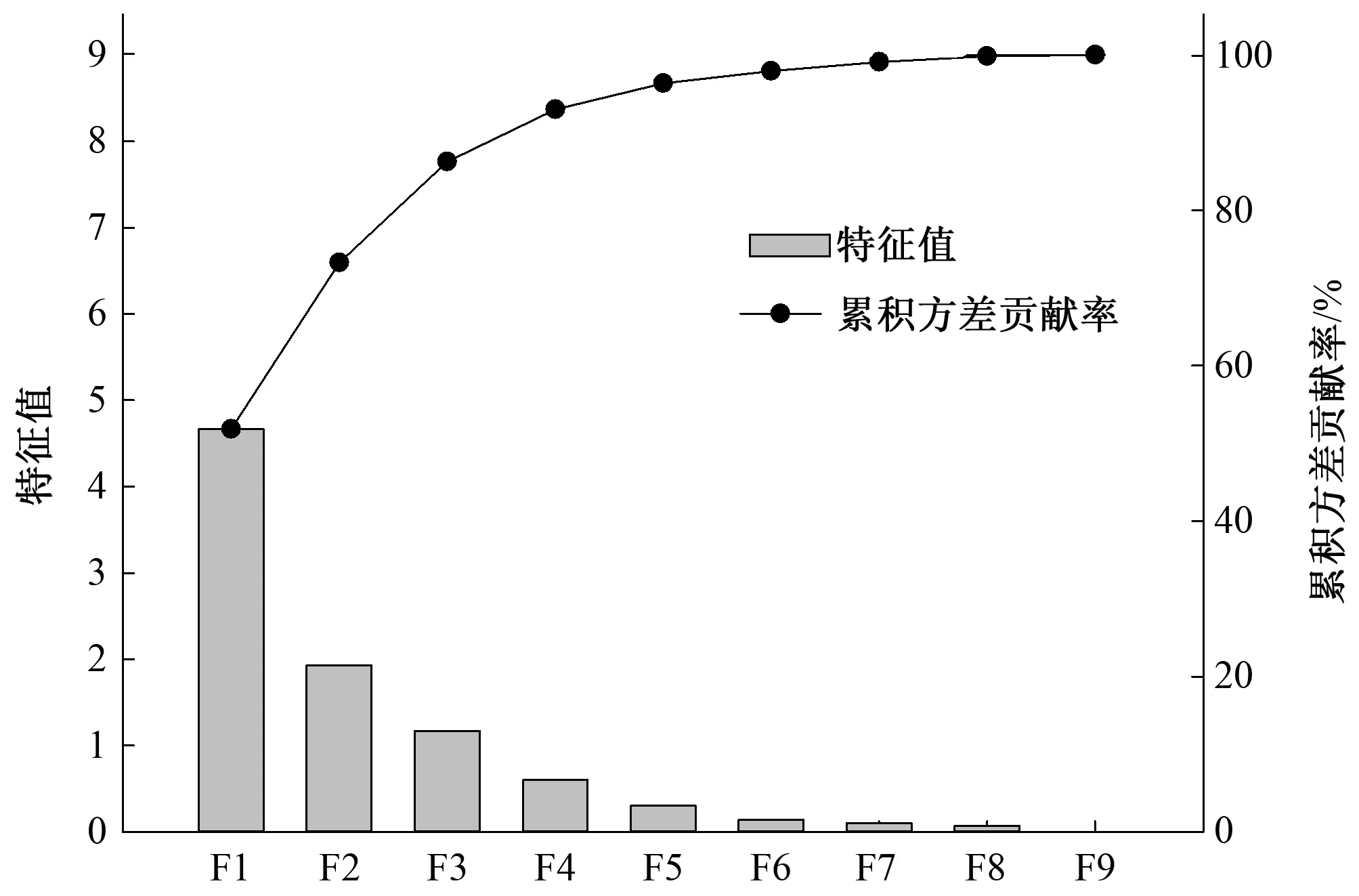
图1 主成分分析结果Fig.1 Results of analysis by PCA

各影响因素与对主成分之间的关系见表2，主成分得分系数矩阵表示了各影响因素与提取前3 个主成分的线性关系[21]，由表2可见，太阳辐射(x1)，日平均气温(x2)，地表土壤温度(x3)，水面蒸发量(x9)，气压(x6)对F1主成分较其他因素所占的比重较大，因此F1可解释为是由太阳辐射(x1)，日平均气温(x2)，地表土壤温度(x3)，水面蒸发量(x9)，气压(x6)构成的综合因子；F2可看成是由相对湿度(x7)和地表土壤含水率(x4)构成的综合因子；主成分F3为降水量(x8)和风速(x5)组成的综合因子。将提取的前3个主成分作为粒子群算法优化支持向量机模型的输入变量，以预测冻融土壤蒸发量。

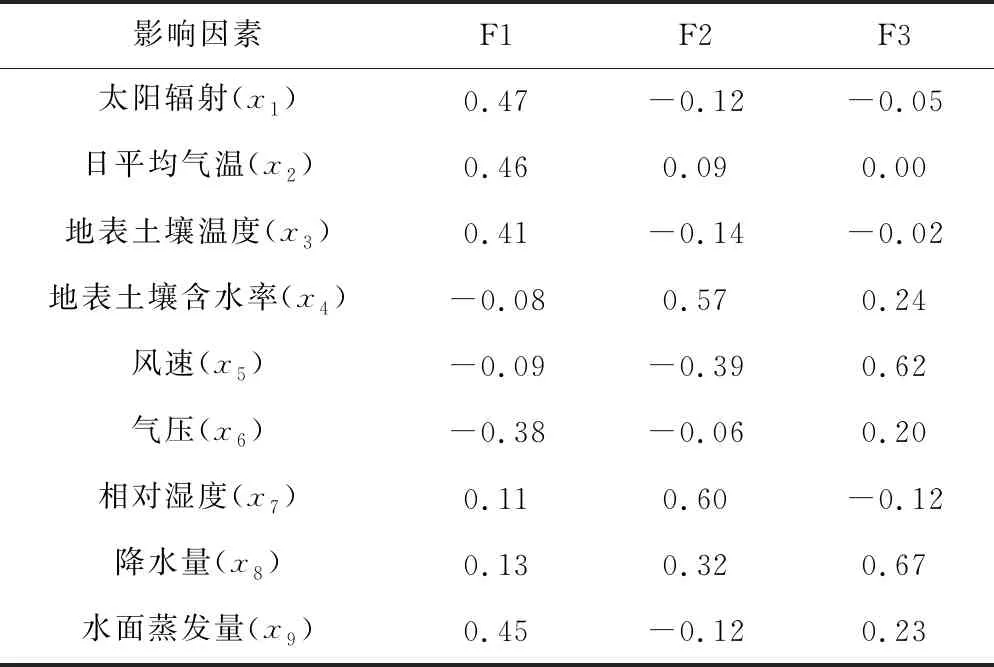
表2 主成分得分系数矩阵Tab.2 Score coefficient weight matrix of principle component

本文选取样本数据中的100组数据进行模型的训练，其余23组作为模型的验证。粒子群算法的参数设定为粒子种群大小为20，最大迭代次数为200，粒子适应度函数为mse函数。经粒子群算法优化后，得到SVM模型的最佳参数值(C=66.870 7，g=2.397 9)。利用LIBSVM工具箱作为SVM建模的基础，基于MATLABR2017a进行编程训练，从而建立的SVM训练模型结构如式(7)所示：

Model = svmtrain (P,T,option)

(7)

式中：Model为本文建立的SVM训练模型；svmtrain为LIBSVM中的SVM训练函数；P为样本输入值；T为样本期望输出值；option为SVM模型的参数及其取值，包括s,t,p,C,g。s表示SVM的类型。本文s为3，采用的是SVM回归模型；t表示核函数的类型，本文t为2，选用RBF函数；p为SVM的损失函数，本文取0.01；C为惩罚因子，g为核函数的参数。

2.3 模型模拟结果与分析

将主成分提取的前3个主成分作为自变量，冻融期土壤蒸发量作为因变量，代入上述训练好的主成分分析-粒子群优化的支持向量机模型(PCA-PSO-SVM)网络，对冻融期土壤蒸发量变化进行预测，得到的训练集和验证集结果见图2。

图2 冻融土壤蒸发量预测值和实测值对比Fig.2 Comparison of forecast and measured values of freeze-soil evaporation

从图2可以看出，在训练模型结果中，模型的模拟值与实测值基本一致，平均相对误差达到12.355 6%，决定系数R2为0.949 8(表3)说明模型的训练精度高，样本数据集的训练效果较好。在检验模型期间，模型的预测值和实测值的平均相对误差达到9.870 4%，达到误差精度要求[29]，决定系数R2为0. 951 3，说明模型的泛化性能效果较好，预测可信度较高，结果误差分析见表3。

由以上模型的训练效果及检验效果可知，采用主成分分析-粒子群算法优化后的支持向量机模型模拟预报的冻融土壤蒸发量，得到的模拟值、预测值与实际值的平均相对误差均小于20%，说明了模型具有较高的模拟精度，泛化能力较好，可用于冻土蒸发量的预报。

3 结 语

本文将主成分分析法和粒子群算法引入到支持向量机模型的参数优化，研究成果为冻融土壤蒸发量的预测提供了新的思路和技术依据。

(1)应用主成分分析法对冻融期日平均气温、太阳辐射、相对湿度、降水量、风速、水面蒸发、水气压以及地表土壤温度和地表土壤含水率等9个影响冻融土壤蒸发量的因素进行了降维分析，消除了各影响因素间的冗余与相关性，提取了更具有针对性的3个主成分，3个成分的累积贡献率达到86.27%。

表3 结果误差分析表Tab.3 The results error analysis of PCA-PSO-SVM model

(2)建立的主成分分析-粒子群算法优化支持向量机的预报模型能准确地进行冻融土壤蒸发量预报，模型训练集中模拟值和实测值的平均相对误差为12.355 6%，决定系数R2为0.949 8；验证集中预测值和实测值的平均相对误差为9.870 4%，决定系数R2为0.951 3。平均相对误差均小于20%，决定系数均大于0.9，证明了所建模型的可行性。文中的研究成果为冻融土壤蒸发量的获取提供了新的思路与技术支撑。