?邓州市粮食产量模型的建立和分析
杨晋

随着经济社会的快速发展和土壤环境污染、工业占用耕地等因素的存在,粮食生产的形势严峻而迫切,给粮食安全带来了一定的挑战。本文以邓州市为参考,运用SPSS软件通过多元线性回归的方法,初步建立邓州市粮食产量模型并分析其影响因素,为相关部门进行粮食产量方面的研究提供参考价值和理论依据。
一、数据准备
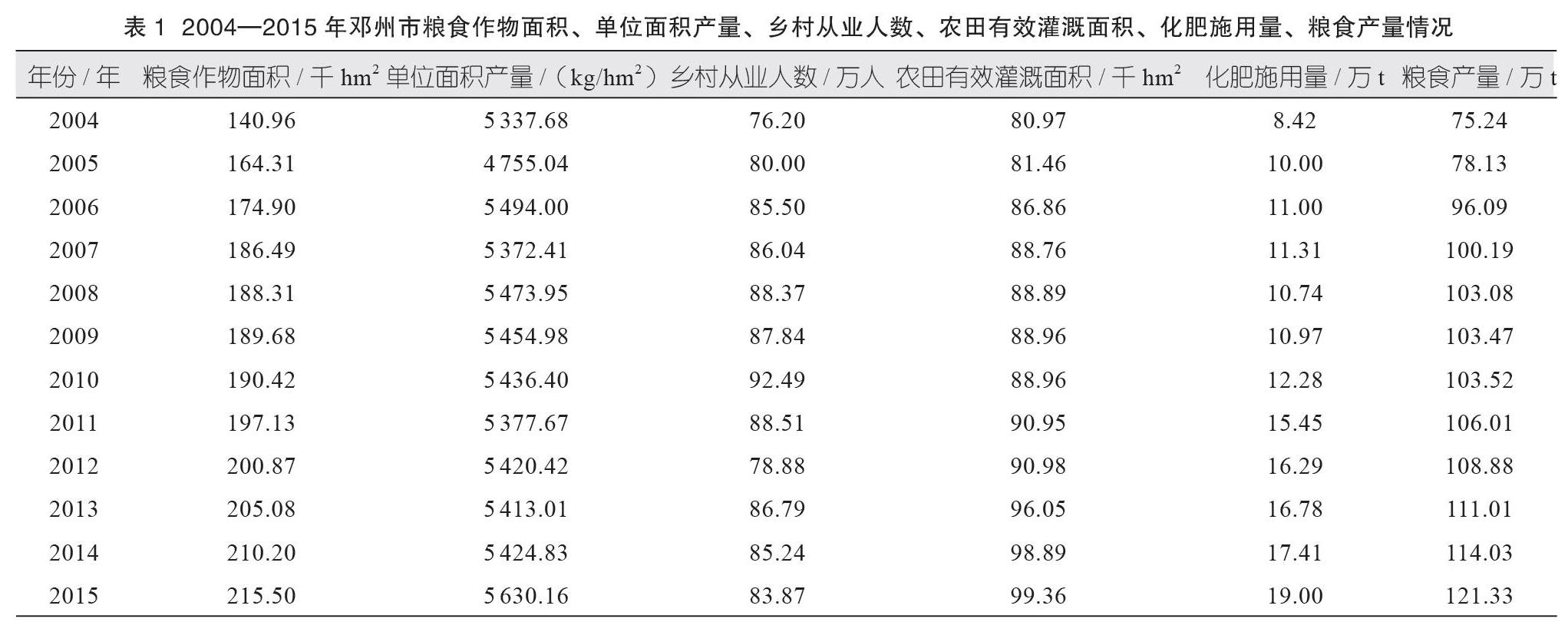
从表1(数据来源《邓州统计年鉴》)可以看出,2004—2015年全市粮食播种面积、农田有效灌溉面积、粮食产量均呈逐年增加的趋势;单位面积产量出现一定程度的波动;乡村从业人数增加至2010年出现峰值,然后下降;化肥施用量基本呈增加趋势。因此,拟初步建立邓州市粮食产量和各影响因素之间的多元线性回归模型,假设粮食产量为因变量y,粮食作物面积、单位面积产量、乡村从业人数、农田有效灌溉面积、化肥施用量分别为自变量x1、x2、x3、x4、x5,因变量和自变量之间存在线性关系。
二、数据分析
(一)对因变量y进行正态性检验
打开SPSS软件,选择菜单分析(A)—描述统计(E)—探索(E),将y选入因变量列表,绘图(T)选择待检验的正态图,对因变量y进行正态性检验。
从表2输出结果得到正态性检验有两种方法,KS检验法和SW检验法。因样本量为12个,小样本适用SW检验法,即统计量0.899,显著水平sig.=0.155>0.05,因此因变量y符合正态分布,可进一步进行回归分析。
(二)因变量y与自变量x1的回归分析
选择逐步回归分析法,主要是为了排除自变量过多产生的干扰,有利于在自变量之间选择出最佳的回归方程。从表3可知:
1.由逐步回归法得出的模型2,剔除了自变量x3、x4、x5的影响,自变量x3、x4、x5与因变量之间不存在显著性差异;而留下的自变量x1、x2偏回归系数的显著性均 <0.05,与因变量之间存在显著性差异。
2. 通过运算过程中得出自变量x1、x2的方差膨胀因子(VIF值)均<5,可认为变量之间不存在多重共线性,模型2成立。
3.根据常量B0为-92.038,粮食作物面积x1的系数为0.543,单位面积产量x2的系数为0.017,粮食产量y与粮食作物面积x1、单位面积产量x2的回归方程
可表达为:
y= -92.038+0.543x1+0.017x2
4.直接得出通徑系数,即自变量x1、x2对因变量y的直接作用分别是P1y=0.838、P2y=0.266。
(三)计算间接通径系数
从皮尔森相关系数输出结果得到自变量与因变量、各自变量间的相关系数。自变量与因变量之间的简单相关系数分别是r1y=0.973、r2y=0.692;各自变量间的相关系数r12=r21=0.509。
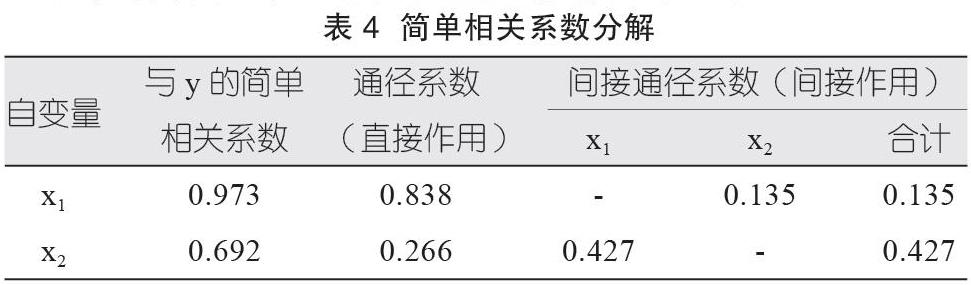
x1通过x2对y的间接通径系数分别为:r12×P2y=0.509×0.266=0.135。x2通过x1对y的间接通径系数分别为:r12×P1y=0.509×0.838=0.427。同时,简单相关系数的值等于通径系数直接作用和间接作用之和,符合统计理论值。整理数据见表4。
三、小结和讨论
(一)在自变量对因变量y的直接影响下,粮食作物面积x1对粮食产量y的影响程度最大,然后是单位面积产量x2。在自变量对因变量y的间接影响下,单位面积产量x2对粮食产量y的影响程度最大,然后是粮食作物面积x1。说明该模型下粮食作物面积和单位面积产量都是影响粮食产量的主要因素。
(二)通过SPSS软件对数据进行统计分析具有专业性、便捷性、可靠性的特点,其输出的结果一目了然,与理论值一致。因此,SPSS软件进行统计分析有一定的推广和应用价值。
(三)该模型下可以得出,要想确保粮食产量的稳定发展,不仅要稳定播种面积、提高单位面积产量,还要加强农业基础设施建设,充分利用好丹江水资源的有效配给,提高农田有效灌溉面积,为邓州市的粮食稳产增产保驾护航。除了以上主要因素,还有环境、气象、农业良种良法配套、农业机械化程度、灾害发生情况等因素也在不同程度上影响着粮食产量,因此,这些因素有待进一步验证。

