常规桥梁抗震设计过程及思路研究
王 磊,陈劲超
(中交第二公路勘察设计研究院有限公司,湖北 武汉 430056)
在高地震烈度区修建高等级公路时,要充分考虑地震作用以保证桥梁设计的安全性,满足全寿命周期。墩柱、桩基作为变形能力较差的压、弯、剪构件,是桥梁结构主要承重构件,因此保证下构足够的承载力与延性是抗震分析的重要内容[1]。部分桥梁设计人员往往注重墩柱的抗震计算,而忽略帽梁、桩基及支座的抗震计算及分析的重要性。本文通过对一座结构简支梁桥的桥墩、帽梁、桩基及支座受力的抗震计算,分析高地震烈度区桥梁的抗震性能计算过程和设计调整思路,提醒设计者必须重视帽梁、桩基和支座的抗震计算。
1 桥梁概况
该算例为跨径4×(5×20)m 的简支桥面连续体系的预应力混凝土小箱梁,半幅桥宽12.75m。所在区域地震动峰值加速度0.4g,反应谱特征周期0.45s。下构为双圆柱墩、桩基础,帽梁和桥墩为C40 砼,桩基为C30砼。1.4m+1.6m 桥墩和桩基直径组合的墩高变化范围在3.9 ~8.2m,1.6m+1.8m 直径组合的墩高变化范围在9.5 ~12.2m,墩高超过7m 时设置一道墩系梁。该桥所在位置钻孔揭示由上至下为粉质黏土、碎石土,16m 以下逐渐进入强风化和中风化泥岩。
2 模型建立及抗震分析
2.1 建立有限元分析模型
使用Midas Civil 有限元分析软件,依据公路桥梁抗震设计细则及公路工程抗震设计规范的相关规定确定偶然荷载组合[2-3]。
抗震计算时应建立上下部各个构件的联系,合理给出支座性能参数。桩基根据每个单元所在位置地质参数转换成地基土弹簧,模拟受力情况对桩基进行约束。依据规范对两个水平方向的地震效应进行组合,采用反应谱法计算E1 及E2 地震作用。该算例桥的第一和第二联、第三和第四联墩高基本相当,因此建立第二、三联计算模型对该桥进行抗震计算分析。模型如图1、图2 所示。
2.2 结构自振特性
E1 地震下构件均采用其毛截面弹性刚度,计算过程中先需要输入计算的阶数。根据规范要求,利用反应谱法查看x、y 两个方向振型参与质量系数是否超过90%。该桥在前20 阶振型下振型参与质量系数均超过90%。
2.3 墩柱效应分析

图1 第二联计算模型
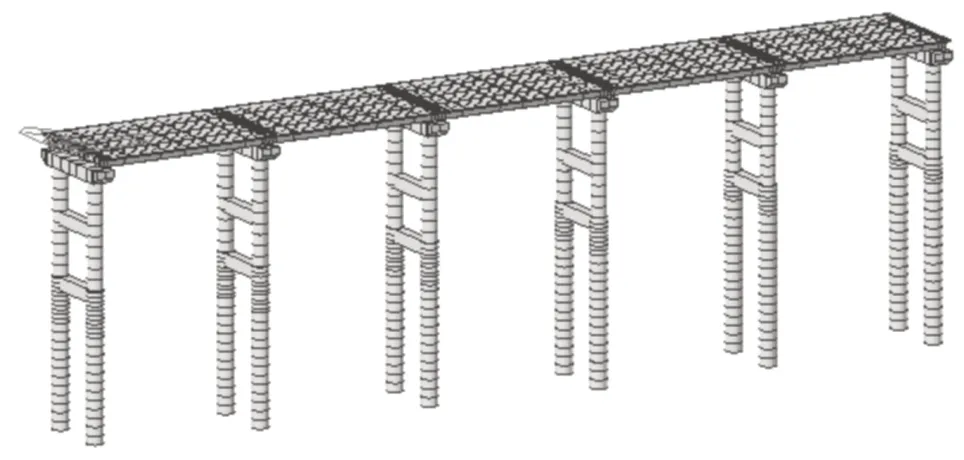
图2 第三联计算模型
考虑到墩柱损伤后结构比较容易修复,故设计时按照延性构件考虑。E1 和E2 地震力作用下,抗震设防的标准采用不同的损伤状态控制,即E1 地震作用下损伤状态:结构基本无损伤,总体反应在弹性范围;E2 地震作用下损伤状态:有限损伤。
结构内力的计算按照实际截面,利用反应谱法进行分析计算。E2 地震下截面抗力按照约束混凝土模型及双折线钢筋模型通过Midas Civil 计算截面的弯矩-曲率曲线;当E2 地震作用下墩顶及墩底处于塑性状态,采用基于位移控制的静力弹塑性分析,核查在地震作用下墩柱位移是否满足要求。
2.4 E1 地震作用下抗震验算
地震作用其方向采用SRSS 组合,振型采用CQC 组合;结构内力按照偶然组合取值。采用反应谱分析E1地震作用下桥梁内力,进行墩柱强度的验算。
该算例中D=1.4m 的墩柱均布32 根Φ28mm 的HRB400 主 筋;D=1.6m 墩 柱 均 布38 根Φ28mm 的HRB400 主筋。根据计算,在E1 地震作用下,墩柱最小压力为1437kN;最大轴压力为4897kN;顺桥向最大弯矩为5311kN·M;横桥向最大弯矩为2034kN·M。桥墩的正截面抗弯承载能力均能满足规范要求。
2.5 E2 地震作用下抗震验算
(1)判断结构是否进入塑性。根据公路桥梁抗震设计细则,采用同E1 地震作用下相同计算方法,通过对E2 地震作用下计算可得两联墩柱最小及最大轴压力、顺桥向及横桥向最大弯矩相应取值。根据取值得出墩柱的弯矩-曲率曲线,然后与桥墩顺桥向的最大弯矩进行比较,判断桥墩底部是否进入塑性状态。桥墩柱在最小轴压(偏安全)作用下,查看弯矩-曲率曲线得出第二联和第三联的初始屈服弯矩分别为3842kN·m 和5284kN·m,均小于桥墩顺桥向的最大弯矩,桥墩底部已进入塑性状态。因此应采用静力弹塑性分析进行抗震验算及分析。
(2)墩顶位移验算。根据抗震设计细则规定进行顺桥向的容许位移计算,常规桥梁的横向位移远小于顺桥向位移,不作为控制因素。该桥通过计算,第二联桥墩顶纵向最大位移0.2401m,小于规范要求值0.465m;第三联桥墩顶纵向最大位移0.2745m,小于规范要求值
0.475m。
(3)墩柱抗剪验算。根据抗震设计细则,需提取桥墩底单元验算数据对塑性铰区域抗剪进行计算。该桥第二联剪力最大为1178.6kN,小于规范要求值2200.5kN;第三联剪力最大为1014.8kN,小于规范要求值2820.5kN。因此E2 地震下,墩柱的塑性铰区域抗剪强度满足规范要求。
2.6 帽梁的抗震验算
在地震作用组合下需对帽梁进行正截面和斜截面的承载力验算;通过模型计算查看帽梁最大弯矩与帽梁抗弯承载力对比,核查帽梁是否满足规范要求。该桥帽梁尺寸为2m×1.5m(宽×高),正截面和斜截面的承载力验算满足规范要求。
2.7 桩基的抗震验算
桩基的约束是根据所在位置的地质情况模拟地基土弹簧的受力模式,然后根据计算结果核查抗弯承载能力是否满足规范要求。对于该桥桩基,D=1.6m 的均 布32 根Φ28mm 的HRB400 主筋,D=1.8m 的均布38 根Φ28mm 的HRB400 主筋。箍筋采用Φ10mm 的HPB300 钢筋,为增加桩基抗剪能力墩顶8m 范围采用双排螺旋箍。通过计算该算例的桩基础的抗弯承载能力不能满足规范要求。
还需对桩基进行斜截面的抗剪承载能力验算,根据钢混规范的计算公式编制表格进行计算,本算例桥桩基础在既有的配筋情况下的斜截面抗剪承载能力不满足规范要求。
2.8 支座的抗震验算
该算例选用板式橡胶支座进行计算,通过计算得出最不利桥墩处的水平地震力,与支座的抗滑承载力进行比较。该桥5 号墩作为最不利位置水平地震力为818kN,而支座的抗滑承载力70.5kN,可知支座的抗滑承载力亦不满足要求。
2.9 延性构造措施验算
按照抗震细则对墩柱潜在塑性铰区域内箍筋最小体积含箍率进行验算,验算时取墩柱的恒载轴力,计算得出允许最小体积含箍率。该算例桥体积含箍率满足要求。
2.10 抗震计算结果分析
经抗震计算,该算例设计方案部分结构尺寸及配筋尚不能完全满足规范要求:
(1)在E1 及E2 地震力作用下,桥墩承载能力均满足规范要求。(2)帽梁抗震计算满足规范要求。(3)该桥桩基础在E2 地震力作用下,抗弯承载能力和抗剪承载能力不能满足规范要求,应对桩基础的配筋或尺寸进行调整。(4)该桥采用常规支座抗滑承载能力不能满足规范要求,应选用专用的抗震型支座重新计算。(5)墩柱在最小轴压作用下墩底已处于塑性状态,应采用静力弹塑性分析进行抗震验算及分析。
3 分析及结论
(1)通过抗震分析得知:墩柱高度不大,更接近于矮墩的受力模式,因此其主要的控制因素应是强度控制,变形次之;此类桥墩是否满足抗震要求首先考虑尺寸及主筋根数。墩柱高度较大,其主要的控制因素应是变形控制,强度次之;此类桥墩是否满足抗震要求首先考虑主筋根数、箍筋直径及间距,然后考虑尺寸。地基土弹簧模拟桩基约束对墩柱抗震计算结果影响较大,因此必须重视桩基受力及约束模拟的重要性。
(2)在地震作用下帽梁受力模式与常规结构受力不同,因此帽梁抗震计算也是抗震计算中应考虑的重要内容。
(3)多数桥梁设计时忽略了桩基的抗震设计。桩基作为桥梁下部最重要的构件之一,其安全及稳定是桥梁抗震计算过程中不可缺少的部分。在抗弯、抗剪均不满足情况下,首先要增加桩基直径,再考虑纵向主筋配筋率,增大箍筋直径后重新验算。桩基抗震计算结果与地基土弹簧模拟、桩基直径、纵向主筋及箍筋等因素有关,因此桩基尺寸及配筋应一桥一设计,重视桩基受力及约束模拟的重要性。
(4)桥梁设计时对桥梁支座的抗滑稳定性验算较容易忽视。对于高地震烈度区常规板式橡胶支座或普通抗震型支座不能满足规范要求,在地震力作用下容易引起主梁脱落,造成二次灾害。作为桥梁最重要的传力受力构件之一,必须通过计算进行支座类型的选取。
(5)在高地震烈度区一般墩底已处于塑性状态,因此必须加强塑性铰区的主筋配筋率、箍筋等级或调整箍筋间距,并通过静力弹塑性分析进一步做结构的抗震验算。墩柱塑性铰区强度也与桩基约束模式有关,桩基的地基土弹簧模拟直接影响墩柱计算结果,因此在计算中应尽可能准确地模拟墩柱所在位置的桩基受力模式。

