数学问题解答

2020年1月号问题解答

(解答由问题提供人给出)

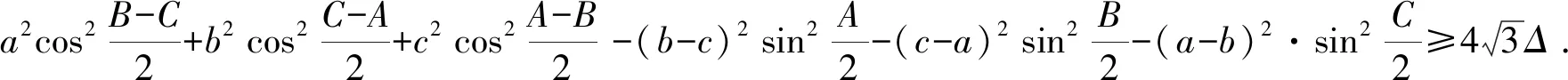
(1)

(河南质量工程职业学院 李永利 467000)

证明记

则(1)式即为

(2)

设△ABC的半周长为p，外接圆和内切圆半径分别为R,r，则由正弦定理可知

因此

=(a-b+c)(a+b-c)

=2(p-b)·2(p-c)

=4(p-b)(p-c)，

同理可得

则由以上三式和恒等式

a+b+c=2p,ab+bc+ca=p2+4Rr+r2，

可得

M-N=4(p-b)(p-c)+4(p-c)(p-a)+4(p-a)(p-b)

=4[3p2-2(a+b+c)p+(ab+bc+ca)]

=4r(4R+r)，

即

M-N=4r(4R+r)

(3)

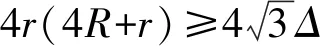
(4)

⟺16R2+8Rr+r2≥3p2,

而由Gerretsen不等式p2≤4R2+4Rr+3r2可知，只需证明

16R2+8Rr+r2≥3(4R2+4Rr+3r2)

(5)

⟺4R2-4Rr-8r2≥0

⟺R2-Rr-2r2≥0

⟺(R+r)(R-2r)≥0

而由Euler不等式R≥2r可知上式成立，故(5)式和(4)式成立，从而(2)式即(1)式成立．

2522如图，凸四边形ABCD内接于圆O，对角线AC,BD相交于点P，△ABP，△DCP的外接圆相交于P,Q，△ADP，△BCP的外接圆相交于P,G,求证：O,P,G,Q四点共圆.

(安徽省岳西县汤池中学 杨续亮 苏岳祥 246620)

证明连接AO,AQ,DO,DQ，

则∠AQD=∠AQP+∠DQP=∠ABP+∠DCP=2∠ABD=∠AOD，

所以A,D,Q,O四点共圆.

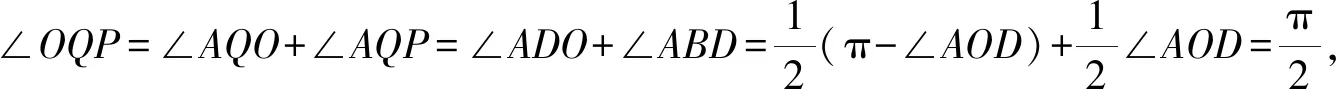
所以∠OQP+∠OGP=π，

所以O,P,G,Q四点共圆.

2523已知a、b、c为正实数，试证：

(*)

(浙江湖州市双林中学 李建潮 313012)

证明记

∑(2a+b)(2a+c)(b+c)2=(2a+b)(2a+c)·(b+c)2+(2b+c)(2b+a)(c+a)2+(2c+a)·(2c+b)(a+b)2．

则由柯西不等式

可有

≥[∑(b+c)]2=4(∑a)2.

①

而

(2a+b)(2a+c)(b+c)2

=(2a+b)(b+c)(2a+c)(b+c)

=[2∑bc+b(b-c)][2∑bc-c(b-c)]

=4(∑bc)2+2(b-c)2∑bc-bc(b-c)2

≤2∑bc[2∑bc+(b-c)2],

从而

∑(2a+b)(2a+c)(b+c)2

≤2∑bc[6∑bc+∑(b-c)2]

=2∑bc(2∑a2+4∑bc)

=4(∑a)2∑bc,

②

联立①与②二式，有

即

(*)

即为所证.

2524设点O,Ia,Ib,Ic分别为△ABC的外心和旁心，R为其外接圆的半径，证明： 6R≥OIa+OIb+OIc.

(安徽省枞阳县宏实中学 江保兵 246700)

证明设s,r分别为△ABC面积和它内切圆的半径，点O,Ia分别为△ABC的外心和边a所对的旁心，ra为△ABC边a所对的旁切圆的半径.作OE⊥BC,IaF⊥BC分别交BC于点E,F，如图所示.

由三角形外心和旁心的性质知，

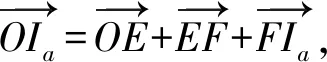
=R2+2Rra,

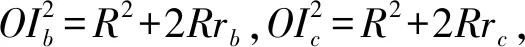
这时，一方面，

ra+rb+rc-r

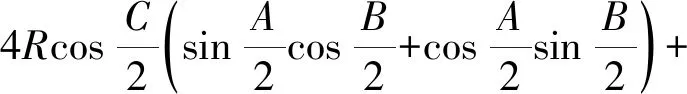
=4R.

即ra+rb+rc=4R+r,

3R2+2R(ra+rb+rc)=3R2+2R(4R+r)

≤12R2. (欧拉不等式：R≥2r)

另一方面，

所以12R2≥3R2+2R(ra+rb+rc)

即 6R≥OIa+OIb+OIc(当且仅当三角形△ABC为正三角形时等号成立).

2525设x,y为实数，满足 (x-4)2+(y-4)2=4 ，求xy的最大值和最小值.

(武汉职业技术学院商学院 邹 峰 430074)

解由x,y为实数且(x-4)2+(y-4)2=4，

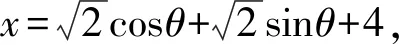
则

2020年2月号问题

(来稿请注明出处——编者)

2526在四边形ABCD中，E是边CD上一点，BE与AC交于点F，射线DF交BC于点G.R是AB延长线上一点，射线RG交CF于点P，AE与PD交于点H.证明：R、F、H三点共线.

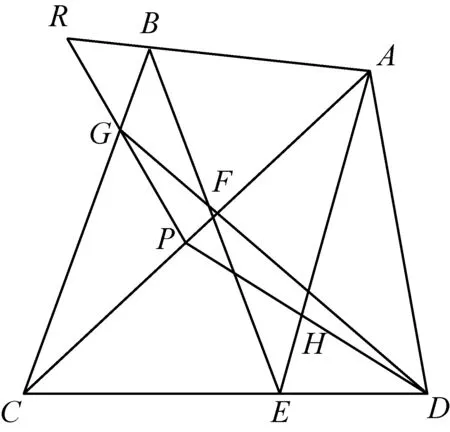
(重庆市合川太和中学 袁安全 401555)

2527在△ABC中，求证:

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000 )

2528试证明tan27°=sec36°-tan36°.

(安徽省六安第二中学 陶兴红 237005 )

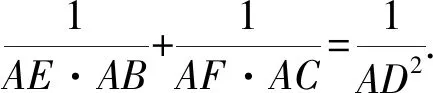
(浙江省慈溪市慈溪实验中学 华漫天 315300)

2530已知a,b,c∈[-2,2],a+b+c=0，求a3+b3+c3的最大值.

(四川省成都华西中学 张云华 610051)