带双目视觉的SCARA机械臂运动学分析及轨迹规划

李旭，裴旭明，刘迪，李浩

带双目视觉的SCARA机械臂运动学分析及轨迹规划

李旭，裴旭明*，刘迪，李浩

（郑州轻工业大学 河南省机械装备智能制造重点实验室，河南 郑州 450002）

为了解决SCARA机械臂因目标位姿变化而引起抓取任务失败问题，给出了一种基于机器视觉目标检测与定位的机械臂控制方法。通过双目相机成像模型实现坐标系之间的转换，利用计算机视觉识别及三维匹配方法，达到对目标物体定位的目的，从而确定机械臂末端执行器的期望位置。结合使用-参数法建立机械臂的运动学模型，通过运动学方程的逆解，得到末端执行器到达期望位置时机械臂各驱动关节的变量参数，然后对其进行轨迹规划仿真，得到了连续且平滑的各关节位移、速度、加速度变化规律曲线，同时使用SCARA机械臂进行装配实验。实验结果表明该系统能够准确、稳定地把物体放到目标位置，完成装配任务，从而为开发机械臂运动控制系统提供重要的参考。

SCARA机械臂；机器视觉；-参数法；运动学；轨迹规划

SCARA（Selective Compliance Assembly Robot Arm，选择顺应性装配机器手臂）机械臂具有刚性高、高速度及安装空间小等优势，广泛应用于抓取放置、装配制造及货物搬运等领域。这类机器人通过精确的示教作业，能完成复杂的点到点的动作，极大提高了生产加工效率。然而传统的示教方法在生产环境和被控对象变化时，容易引起目标位置和姿态偏差，进而导致机器人任务执行失败[1]，为了准确进行目标识别，使机械臂能自动调整位姿，使其在装配过程中运动更平滑、平稳，国内外学者做了大量相应研究。基于双目视觉技术的机械手臂目标定位系统，运用运动学分析和轨迹规划，借助LabVIEW、Adams、MT-ARM等仿真软件，依据雅可比函数、-（Denavit-Hantenberg）法等理论，对平行四连杆机构的码垛机器人的运动控制与视觉抓取、进行运动学和视觉算法的研究，建立视觉自适应机械臂抓取系统，有效的解决了生产线上码垛作业问题[2-4]；另外利用PIEPER准则推导逆运动学的封闭解，在笛卡尔空间中通过对空间插值点的优化减小轨迹偏差，实现机械臂执行机构的轨迹优化[5-6]。还有在避开机械臂奇异位姿情况下能够实时计算出多关节中每个关节的速度并进行控制，有效解决因传统插补方法使得机械臂运行缓慢的问题，实现对机械臂的正、逆运动学以及轨迹规划仿真分析，大大的提高了机械臂运行效率[7]；针对多自由度杆件机构的机械臂在笛卡尔空间中对空间插值点，推导逆运动学的封闭解、解决了机械臂运动轨迹偏差较大的问题[8-9]；甚至采用改进的-法建立其运动学方程在Matlab Robotics Toolbox环境下，来验证运动学方程的正确性[10-12]，这都为后者提供了一种更有效的工业机器人运动学的研究方法。

本文以SCARA机械臂为研究对象，将视觉算法应用到目标位置的识别和定位上，从而得出末端执行器的期望位置；进而基于运动学理论对机械臂逆运动学方程进行求解，计算出末端执行器达到预期位置时机械臂各个驱动关节的变量参数，对其进行轨迹规划仿真，得到各个关节运动规律曲线图，对仿真结果进行分析以及实验验证。

1 目标的识别与定位

1.1 视觉机械臂抓取系统

视觉装配平台如图1所示，由双目视觉系统、机械臂控制系统、机械臂本体及装配平台组成。工作原理如图2所示，视觉系统由双目相机负责采集图像传送到计算机里进行图像处理，以完成目标的识别与定位，得到目标的位置信息。机械臂控制系统将这些信息计算出机械臂各自由度的变化量，驱动伺服电机转动相应角度，使得末端执行器到达目标位置，实现对目标物体的准确装配，同时在机械臂上安装传感器形成闭环控制，保证机械臂的控制精度。

图1 双目视觉机械臂装配平台组成

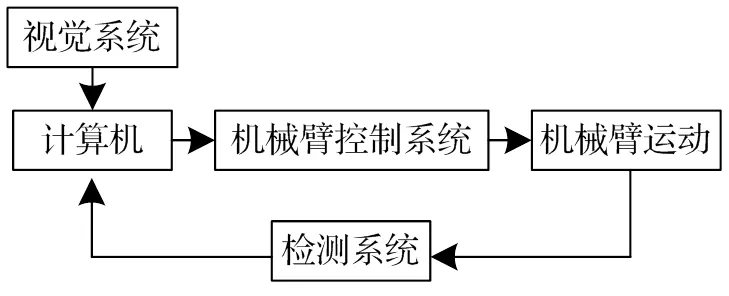
图2 实验系统工作原理图

1.2 目标的识别与定位

识别定位目标物体在图像中的坐标，是实现视觉对机械臂运动引导的关键。而在图像检测和识别的算法中，图像的质量和一些干扰信息是影响算法处理精确的主要影响因素。因此，在对图像进行目标检测识别之前，首先对相机采集到的图像进行灰度化处理，其次采用中值滤波及高斯滤波进行预处理，去除或者降低无关信息的干扰，然后通过三维匹配方法，结合相机内外参数和三角测距原理，最终计算得到目标的坐标[13-14]。

三维匹配是寻找同一空间点在不同相机采集到的图像像素间的对应关系，其利用质心作为匹配点得到目标视差的估计值，再依据该值来设定搜索范围，在一幅图像中搜索与另一幅图像目标质心相似度最高的匹配点从而得到视差。双目相机采集的图像之间灰度值的接近程度用r,y,p表示为：

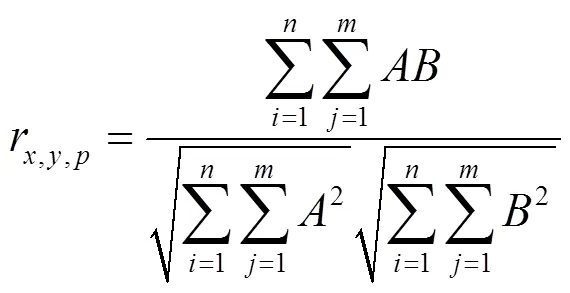
搜索范围可表示为：

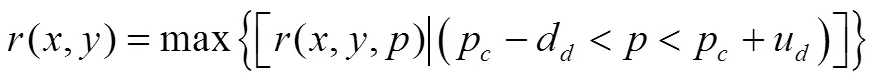
式中：p为匹配时得到的视差值；u、d为对应视差值的上偏移量和下偏移量。

结合三角测距原理，以左相机焦点为坐标系原点，可计算得目标在空间中的三维坐标为：

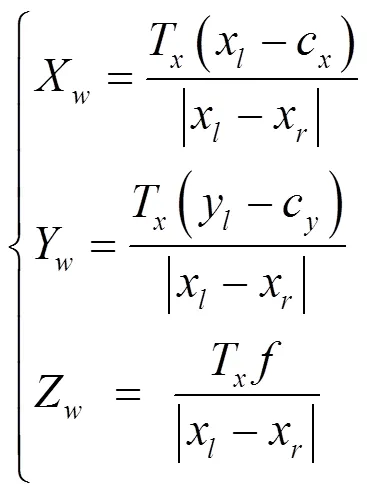
式中：T为双目视觉相机的基线长度；（x, y）和（c, c）分别为左相机图像坐标系的形心坐标和校正后的坐标；为左目相机焦距；x为右目相机在图像坐标系的横坐标。

通过得到目标物体上某点在左右相机中拍摄到的图像中的像素坐标，可以获得该点在空间中的三维坐标，进而实现三维重建和识别。

2 机械臂运动学分析

2.1 机械臂D-H模型

为解决机械臂的几何特性不易描述和计算问题，20世纪50年代，Denavit和Hantenberg研究出一种描述机械臂的-参数法，降低了运动学的计算量[15]。采用-参数法建立运动学坐标系模型，运用4×4的齐次变换矩阵代替复杂的运动学计算。-参数法以机械臂基座为初始坐标系，各关节旋转轴轴线方向为坐标系的z向，轴z与z1的公垂线方向为坐标系的x向，y则可通过右手定则确定。依据该方法建立如图3所示的SCARA机械臂坐标系模型，得到如表1所示的-参数。

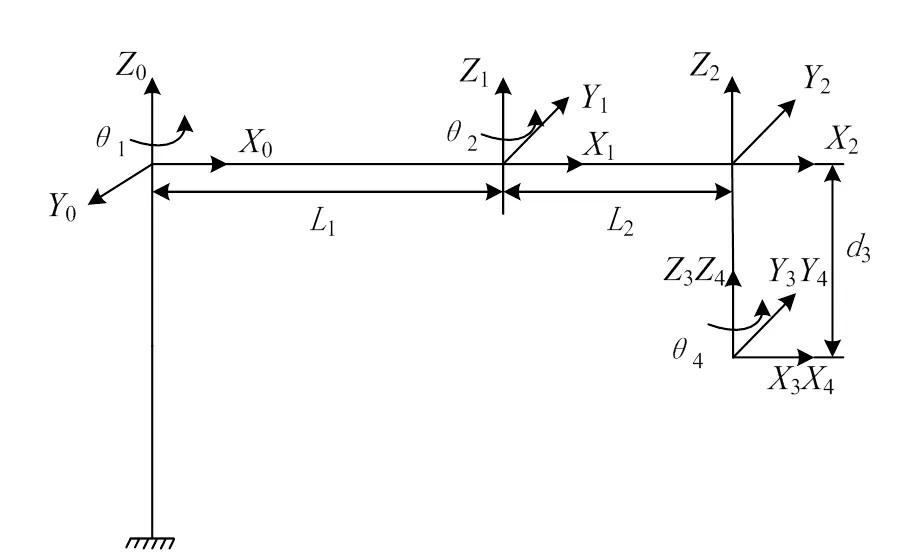
图3 SCARA机械臂运动学坐标系模型

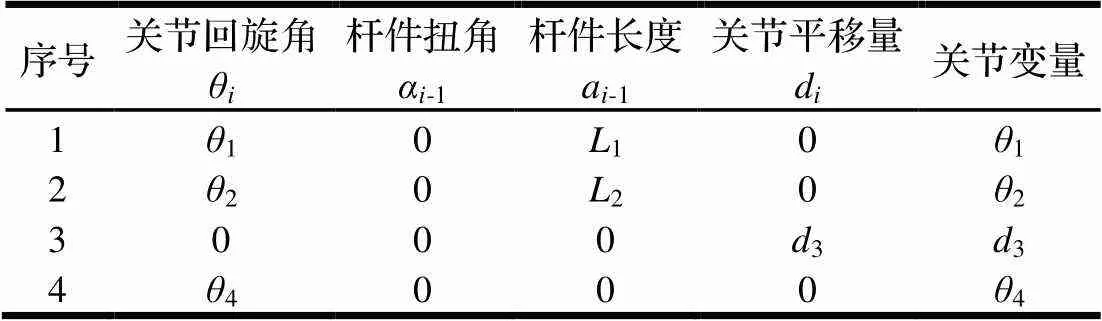
表1 运动结构参数

注：1＝0.25 m；2＝0.15 m。

2.2 机械臂正运动学分析

为了获得末端执行器的位姿，需要通过已知驱动关节参数对机械臂正运动学进行分析。根据机械臂连杆的坐标变换法则，相连的两连杆间的关系可由齐次变换矩阵表示为：

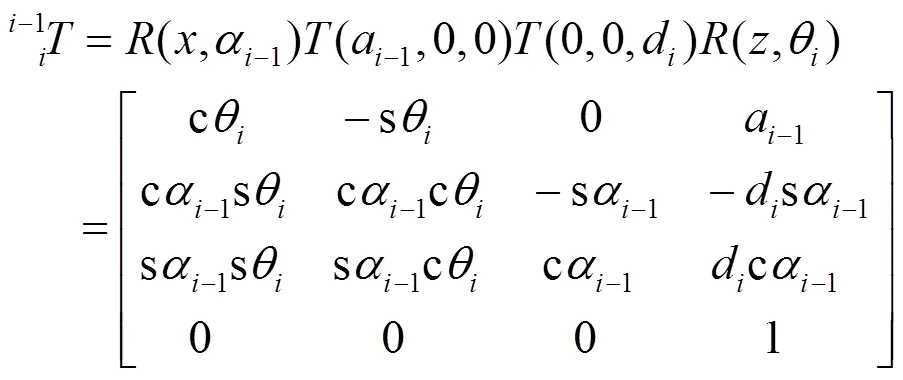
式中：cθ＝cosθ；sθ＝sinθ；sα-1＝sinα-1；cα-1＝cosα-1。

将SCARA机械臂-参数代入式（4）可得到四个相邻关节坐标系的齐次变换矩阵为：

由式（5）中将各个连杆变换矩阵依次相乘，即可得正运动学方程：

式中：[n o a]、[n o a]、[n o a]分别为末端执行器三个坐标轴的单位矢量相对于基座坐标系的轴上的投影分量；[p p p]T为末端执行器相对于基座的平移。

式（6）即为SCARA机械臂变换矩阵，指的是末端相对基的位姿，也是研究机械臂关节运动的重要方程。将式（5）各矩阵代入式（6），由两矩阵对应元素相等即可得到机械臂末端执行器位置求解方程为：

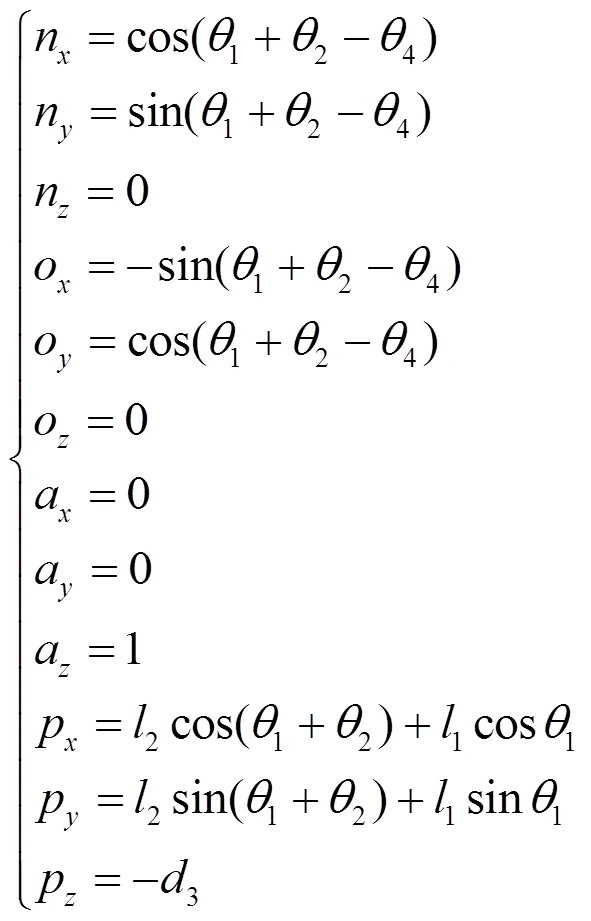
2.3 机械臂逆运动学分析

机械臂逆运动学方程的解就是在给定目标期望位姿时，求得末端执行器达到预期位姿时机械臂各个驱动关节的变量参数。

（1）求关节变量1

令式（8）中组成方程：

解式（9）可得：

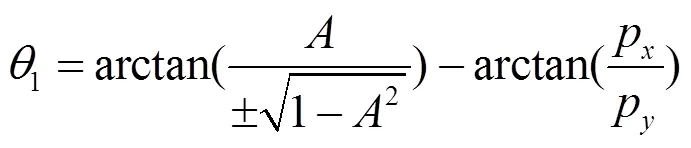
（2）求关节变量2

将1代入式（9）可得：

（3）求关节变量3

由式（8）可得：

（4）求关节变量4

由式（8）可得：

解式（13）可得：

3 SCARA机械臂轨迹规划

使用合适的轨迹规划方法，可以提高机械臂运行过程的稳定性，从而提高机械臂的工作效率以及使用寿命[16-17]。轨迹规划实质上就是各驱动关节的位移、速度、加速度的变化量。

3.1 轨迹规划算法

轨迹规划分两种情况，一种是关节空间规划，另一种是笛卡尔空间规划[18]。前者能够避免求逆解，运算量小，容易避免机械臂的奇异位置；而后者运算量大，避免机械臂奇异位置比较困难。本文主要针对SCARA机械臂在关节空间中对点到点运动使用五次多项式插值算法，确保其平稳无震荡运动。使用五次多项式插值算法时，机械臂初始点和终止点的关节参数分别为θ、θ、t和t，在初始位置和终止位置速度，加速度都为0的前提下，各关节变量与时间关系的五次插值函数()为：

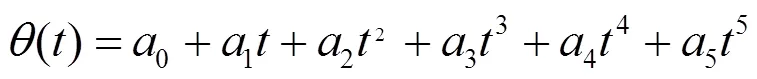
对式（15）求导，可以得到变化的速度和加速度，分别为：

需要满足的约束条件为：

解式（17），可得：

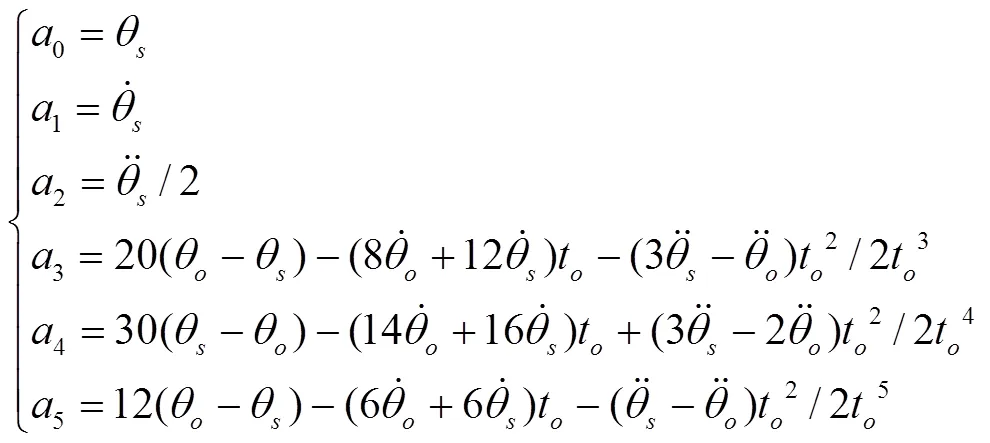
3.2 SCARA机械臂仿真分析

根据SCARA机械臂结构参数，使用MATLAB Robotics Toolbox中的Link函数创建SCARA机械臂模型[19]。Link函数为L=Link（[Alpha A Theta D Sigma], Convention），其中：Alpha、A、Theta、D分别对比杆件扭角、杆件长度、关节回旋角、关节平移量；Sigma为0代表旋转关节、非0代表移动关节；convention取standard代表采用标准-参数，modified代表采用改进的-参数。

由表1可知，使用Link和SerialLink函数创建SCARA机械臂模型，并命名为“SCARA机械臂”，如下：

L1=Link([0 0.25 0 0 0], ’standard’);

L2=Link([0 0.15 0 0 0], ’standard’);

L3=Link([0 0 0 0 1], ’standard’);

L4=Link([0 0 0 0 0], ’standard’);

bot=SerialLink([L1 L2 L3 L4],

'name','SCARA机械臂');

通过plot函数将机械臂模型显示出来，如图4所示。

图4 SCARA机械臂模型

使用MATLAB仿真软件的jtraj五次多项式插值函数即可得到机械臂模型的规划轨迹。其调用格式为[q,qd,qdd]=jtraj(T1,T2,t)，其中：q为从状态T1=[0 0 0 0]到T2=[pi/2 0 pi/4 -pi/4]的关节空间规划轨迹；qd和qdd为其速度和加速度；T为各关节角度；t为仿真时间长度。实验设置机械臂从T1～T2的运行时间是2 s，得到机械臂末端执行器的运行轨迹如图5及各关节角位移、速度、加速度的变化曲线如图6所示。在0～0.4 s驱动关节1、3的角加速度平缓增加，在0.4～1 s角加速度平缓减少；在0～0.4 s驱动关节4角加速度反向平缓增加，在0.4～1 s角加速度反向平缓减少，关节变化规律曲线在1～2 s角加速度的变化与0～1 s大小相等方向相反。通过速度曲线可以看到在加速度平缓增加的时候，速度逐渐变大，到加速度变化为零时达到最大值，然后逐渐减少至零。通过位移曲线可以验证速度加速度曲线的正确性。

图5 机械臂末端执行器运动轨迹

综合分析可知机械臂从初始状态到末尾状态运动过程中工作正常、运动平稳，速度和加速度曲线平滑无突变，表明其运行稳定，轨迹规划合理，可以达到期望的效果。

4 机械臂物块装配试验

为了验证前述方法的有效性，在图1所示的试验平台上进行视觉抓取装配试验。该试验平台视觉系统包括CCD相机、镜头及图像采集卡。相机采用东芝TELI工业摄像头，其CCD阵列含有像素个数为768×576，水平析像力为570行。镜头采用Tamron CCTV镜头，镜头焦距范围为4～12 mm。图像采集卡使用Matrox Morphis四通道图像采集卡，其有支持PCI、PC/104-plus等多路总线。

将机械臂运动起点位置设置为仿真的T1点，目标物体放置在机械臂运动的终点位置上，其为仿真的T2点。通过控制系统控制机械臂进行装配试验，结果说明在给定路径点的情况下能够保证机械臂达到预期的位置，并且其在运动过程中平滑、稳定，和仿真结果表现的一致，验证了轨迹规划算法在机械臂实际运动中的有效性和可行性。机械臂装配过程如图9所示。

图6 关节变化曲线

图7 机械臂装配过程

5 结论

针对SCARA机械臂在装配过程中运动的稳定性，经视觉定位和轨迹规划得到以下结论：

（1）由视觉系统预处理后的图像结合三维匹配法及三角测距原理，可以准确得到目标物体的坐标；

（2）经逆运动学方程得出的解，可以获得机械臂各个驱动关节的变量参数，并对其进行轨迹规划仿真，结果表明机械臂位移、速度、加速度的变化曲线是平滑、无突变，证明其运动过程是稳定的。

（3）通过机械臂物体装配实验表明该系统能够准确、稳定地把物体放到目标位置，完成装配任务，为开发机械臂运动控制系统提供重要的参考。

[1]桑杲，俞经虎. 基于MATLAB的采摘手末端执行器的分析及优化[J]. 机械，2017，44（12）：36-40.

[2]Wang Y，Lv H Y，Wang N. A Machine Vision System for Measurement of Mechanical Parts Based on LabVIEW 2012[J]. Advanced Materials Research，2013（834-836）：1186-1189.

[3]Corke P. I. A robotics toolbox for MATLAB[J]. IEEE Robotics Automation Magazine，1996，3（1）：24-32.

[4]张燕超，崔吉. 全方位移动机器人动力学研究[J]. 机械， 2019，46（3）：24-27，69.

[5]曹成涛，许伦辉，赵雪，孙永嘉. 四轴工业机器人运动控制与视觉码垛[J]. 机械设计与制造，2016（11）：158-161.

[6]熊艳梅，杨延栋. 码垛机器人运动学分析与仿真[J]. 机械，2015（1）：62-66.

[7]云洋，宋华，徐炳吉. 六自由度工业机械臂运动学仿真研究[J]. 机械科学与技术，2018（8）：1167-1176.

[8]Jing H，Wang X L，Liu D S，et al. A New Method for Solving Inverse Kinematics of an Industrial Robot[C]. International Conference on Computer Science Electronics Engineering，10.1109/ICCSEE.2012.8.

[9]李宏强，底剑豪，等. 平面3R操作臂动力学分析[J]. 机械，2011，38（12）：47-50.

[10]孙亮，马江，阮晓钢. 六自由度机械臂轨迹规划与仿真研究[J].控制工程，2010，17（03）：388-392.

[11]Malekabadi A J，Khojastehpour M，Emadi B，et al.Development of a machine vision system for determination of mechanical properties of onions[J]. Computers Electronics in Agriculture，2017（141）：131-139.

[12]王鹏程，沈惠平，孟庆梅，等. 一种冗余自由度机械臂逆运动学解析算法[J]. 机械科学与技术，2016，35（5）：706-710.

[13]Viana I，Bugarin F，Cornille N，et al. CAD-guided inspection of aeronautical mechanical parts using monocular vision[J]. Proceedings of SPIE - The International Society for Optical Engineering，2015：9534.

[14]Lian H，Xiwen L，Shan Z，et al. Plant recognition and localization for intra-row mechanical weeding device based on machine vision[J]. Transactions of the Chinese Society of Agricultural Engineering，2013，29（10）：12-18.

[15]Wen S H，Ma Z Y，Zhao Y S，et al. The study of NAO robot arm based on direct kinematics by using D-H method[C]. Ukacc International Conference on Control，2014.

[16]Huang G S，Tung C K，Lin H C，et al. Inverse kinematics analysis trajectory planning for a robot arm[C]. ASCC 2011 - 8th Asian Control Conference - Final Program and Proceedings，2011.

[17]Potts A S，Da Cruz J J. Kinematics Analysis of a Quadruped Robot[J]. IFAC Proceedings Volumes，2010，43（18）：261-266.

[18]蒋伟，袁亮. 串联抓取机械臂运动轨迹规划算法研究[J]. 机械设计与制造，2019（7）：106-110.

[19]曾剑，林义忠，廖小平，等. 6R型喷涂机器人运动学分析及仿真[J]. 机械设计与制造，2010（6）：145-14.

Kinematics Analysis and Trajectory Planning of SCARA Manipulator with Binocular Vision

LI Xu，PEI Xuming，LIU Di，LI Hao

( Henan Key Laboratory of Intelligent Manufacturing of Mechanical Equipment, Zhengzhou University of Light Industry, Zhengzhou450002, China)

A control method for SCARA manipulator is presented on the basis of the detection and location of machine vision to solve the robotic gripping failure caused by the change of target pose. The coordinate system is transformed by employing binocular camera imaging model, and the location of target object is realized through computer vision recognition and three-dimensional matching method to determine the expected position for the end-effector of the manipulator. The variable parameters of each driving joint while the end-effector reaching the expected position is obtained by establishing kinematics model though-parametric method and solving the inverse kinematics equation. Then, a set of continuous and smooth curves of joint displacement, velocity and acceleration are obtained by simulation. Meanwhile, the assembly test on the SCARA manipulator is carried out. The results indicate that the system is able to move the object to the target position and complete the assembly mission accurately and stably, which provides important reference for the development of the motion control system for manipulators.

SCARA manipulator；machine vision；-parameter method；kinematics；trajectory planning

O311.2

A

10.3969/j.issn.1006-0316.2020.02.002

1006－0316 (2020) 02－0007－08

2019－10－08

国家自然科学基金资助项目（51775517）；河南省科技攻关项目（102102210134）

李旭（1994－），男，河南驻马店人，硕士研究生，主要研究方向为机器人控制技术。

裴旭明（1962－），女，河南南阳人，硕士，教授、硕士生导师，主要研究方向为机械动力学与控制。