孔中心距对限流孔板压降的影响
王天豪,吉华,李倩,段宗幸,吴孙珂
孔中心距对限流孔板压降的影响
王天豪,吉华,李倩,段宗幸,吴孙珂
(四川大学 化学工程学院,四川 成都 610065)
为研究多级限流孔板(MHO)中布孔的中心距对压力降的影响,先根据设计标准计算出多级限流孔板的基本结构参数。在此基础上,基于Fluent的Standard-湍流模型,建立了流体的三维数值计算模型,对降压作用最大的第一级限流孔板(MHO-1)的压降1进行了调查。数值计算结果表明:等间距布孔时,MHO-1、第二级限流孔板(MHO-2)的孔中心距分别为28 mm、30 mm时,1最大;MHO-1上孔中心距不变时,只改变等间距布孔的MHO-2上第1层孔中心距2c1和第2层孔中心距2c2,2c1的变化比2c2的变化对1的影响更加明显;总体趋势是1随着MHO-1、MHO-2上孔中心距的增大而减小。
限流孔板;孔中心距;数值计算;压降
限流孔板在管道中可作为节流元件用来限定流量和降低压力,许多学者关注到了孔板几何结构对压降的影响。Barros Filho J A等[1]研究了节流孔坡度对压降的影响,并得到较大坡度压降较大的结论。李琳等[2-3]采用Standard湍流模型,分析孔板间距和雷诺数对管路局部阻力的影响,研究表明:随着雷诺数的增大,局部阻力会增大,最后会趋于一个定值,对于一定的孔板间距范围,两孔板间距越小,影响越明显,局部阻力越小。于洪仕等[4]研究了节流孔前后倒角对多孔孔板流量计流场特性的影响,得到节流孔前倒角是影响永久压力损失的关键因素,节流孔后倒角对尾流流场具有调整作用的结论。K H Yau等[5]研究了开孔率对压降和流动稳定性、均匀性的影响,开孔率为0.5的较0.7的压降大,但流动稳定性较差。王慧锋等[6]针对单级孔板,在孔中心距和等效直径比一定的情况下,对不同孔分布的压损系数和流出系数进行比较,发现开孔较少、有中心孔以及环形分布的孔板压损系数更小,流体流动特性更稳定,但未考虑孔板级数以及孔板上孔中心距对压降性能的影响。
本文基于Fluent软件的Standard湍流模型,研究了多级限流孔板的内部流场流动特性,并从原理上分析了产生压降的主要因素,最后得出孔中心距对压降性能的影响规律。
1 计算模型
1.1 几何模型
表1为工况条件,根据标准[7],得到如表2的主要计算结果。

表1 工况条件
孔板的基本几何结构如图1所示,(b)~(e)表示了MHO-1、MHO-2、MHO-3、MHO-4的布孔方式,其中d下标第一个数字代表MHO-,表示中心距,表示其他孔与中心孔的层数,如1c1表示是MHO-1第一层邻近孔与中心孔的中心距。如果孔板开孔分布和数目随机选择,研究工作将会非常复杂[6],节流孔的分布多为对称分布[6,8-9],所以本文布孔方式为:根据开孔数目,布孔尽可能对称,选择矩形或环形分布,如图1(b)(c)所示。
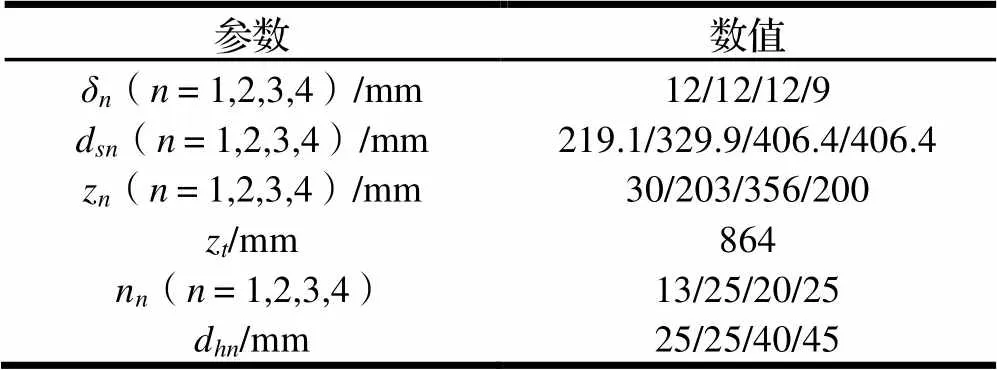
表2 设计结果
表中:MHO-(=1,2,3,4)为第级孔板;δ为MHO-厚度;sn为MHO-直径;z为孔板各个连接件长度;z为MHO总体长度;n为MHO-的数目;hn为MHO-上的节流孔孔径。
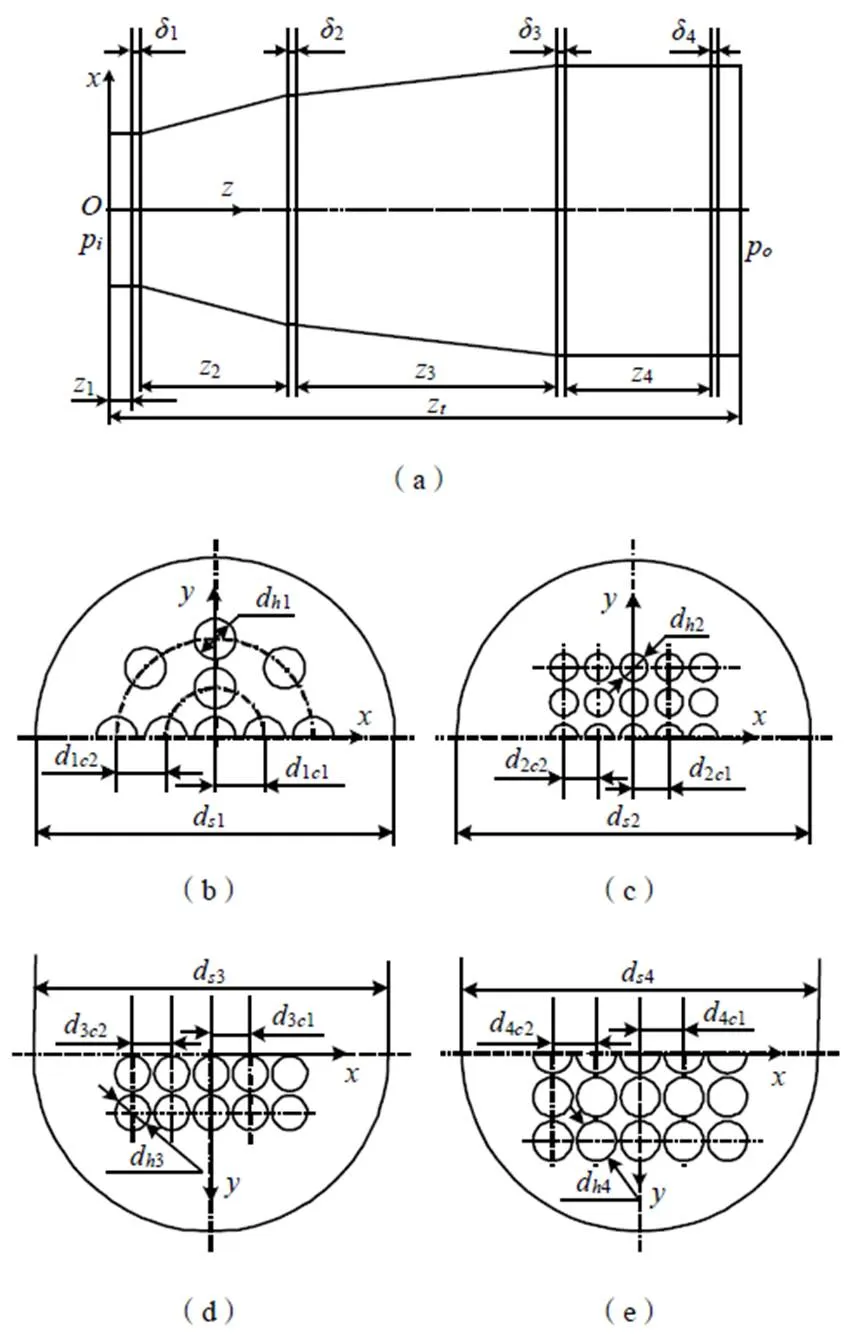
图1 孔板的基本几何结构
基于计算结果和布孔方式,采用UG软件建立了多级限流孔板的流体计算域的三维几何模型,并使用ICEM CFD进行结构性网格划分。
1.2 FLUENT求解器设置
如图1(a)所示,设定压力进口边界条件和压力出口边界条件p;壁面采用无滑移条边界件;由于介质为气体,密度较小,因此忽略重力选项,物性设置为ideal-gas;压力与速度耦合选用SIMPLE;动量离散方式选用Second Order Upwind;湍流模型采用Standard模型,Standard模型中的5个常数采用c=0.9、1=1.44、2=1.92、σ=1.0、σ=1.3[10]。
2 结果分析
为了便于数据对比、分析,将沿着轴的压力p和沿以入口处为坐标原点的轴向距离化为无量纲形式,Z=/(1+1+2),P=p/p。
由于研究过程中所涉及的孔板开孔数目较少,每级限流孔板的孔中心距数目为2。等间距是指在MHO-上d1=d2=const,否则为非等间距。由于压降主要发生在MHO-1、MHO-2,尤其是MHO-1的压降1,因此本文重点分析MHO-1、MHO-2上孔中心距对1的影响。所研究的三维模型中3c1=3c2=45 mm、4c1=4c2=50 mm固定不变,只改变MHO-1、MHO-2上孔中心距的大小。
2.1 流场压力分布
如图2所示,流体流经孔板后,节流孔内发生压力骤降,这是由于充满管道的流体流经孔板时,流体在孔板节流孔处收缩,流速增加,流体静压降低,会在孔板两侧产生很大的压差。
2.2 MHO-1上等间距时孔中心距大小对压降∆p1的影响
因为靠近MHO-2入口处的流体压力又开始发生剧烈变化,所以图3、4和表3、4中压力数据来自于Z∈[0~0.8]。
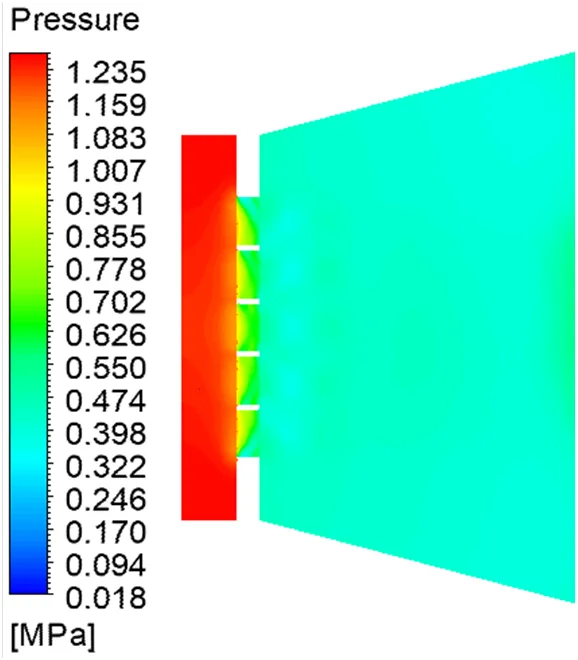
图2 MHO-1前、后静压
以图3中孔中心距为28-28-30-30(依次表示1c1、1c2、2c1、2c2的大小)下P随着Z的变化曲线为例,可以看出P先骤减,然后恢复。这是由于运动流体的惯性,流经节流孔后保持原来的流动方向,在孔板出口形成最小流束收缩截面,此处流速最大,压力最低。之后流束渐扩,压力逐渐升高,直至流体充满管道,压力恢复到最大值,研究模型MHO-1、MHO-2板间距不足以使流体得到完全恢复,又由于孔在孔板上分散分布,根据文献[11]中的双股射流理论,流体流经多孔限流孔板后在管道中形成受限性多股射流,多股射流间形成会聚区,最终合二为一进入联合区。此外,由于卷吸现象的存在,会聚区内形成射流间回流区,各股射流间回流区中有大量的漩涡存在,导致了永久压损。契合了图3中同一曲线上P最大恢复值小于Z=0时n的值。
如图3所示,随着MHO-1、MHO-2上孔中心距的增大,(P)min在逐渐增大,且曲线上平缓处与(P)min的差值在逐渐减小,当布孔间距为28-28-30-30时,(P)min=0.299,此时1最大。当布孔间距为34-34-30-32时,(P)min=0.431,此时1最小。随着MHO-1、MHO-2上孔中心距的增大,压力恢复时波动在逐渐减小,这说明多孔孔板上孔中心距在一定范围内增大时,会使得流体分布更加均匀,减少了涡流的形成和湍流摩擦,降低了动能损失,流动稳定性增强,在相同的计算条件下,永久压力损失要低一些。
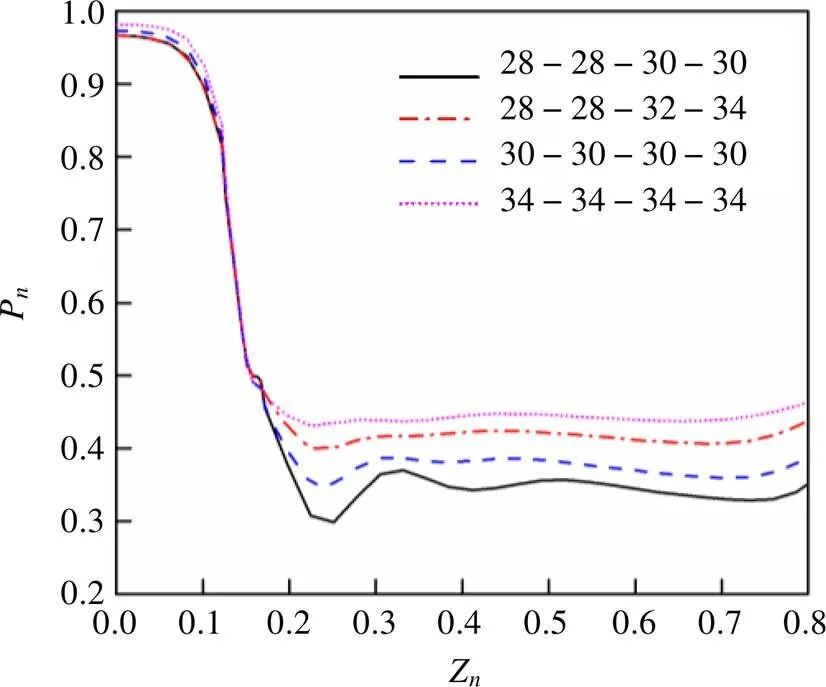
图3 MHO-1等间距布孔对∆p1的影响
为了比较孔中心距对1的影响,定义p为压降比r=1/i。
从表3可以看出,当MHO-1上孔中心距固定不变且MHO-2上等间距时,1随着2c1、2c2的增大而减小,如布孔间距为28-28-34-34和28-28-30-30时前者1较后者减少16.27%;当等间距的MHO-2上孔中心距固定不变时,1随着MHO-1上孔中心距的增大而减小,如布孔间距为34-34-30-30和28-28-30-30时前者1较后者减少12.37%。当非等间距的MHO-2上孔中心距固定不变时,1随着MHO-1上孔中心距的增大而减小,布孔间距为30-30-32-34时除外;当MHO-2上非等间距且MHO-1上孔中心距不变时,1随着MHO-2上孔中心距的增大而减小。在等间距的MHO-1上孔中心距不变的情况下,只改变等间距的MHO-2上2c1和2c2两者任一的大小,2c1的变化比2c2的变化对1的影响明显的多,如布孔间距为30-30-30-32和30-30-32-32时,前者较后者2c1减小了2 mm、1增大了3.86%,但是布孔间距为30-30-32-34和30-30-32-32时,前者较后者2c2增大了2 mm、1减少了0.32%。
2.3 MHO-1上非等间距时孔中心距大小对压降∆p1的影响
如图4所示,MHO-2上孔中心距的增大,(P)min在逐渐增大且曲线上平缓处与(P)min的差值在逐渐减小,当布孔间距为30-32-30-30时,(P)min=0.376,此时1最小,当布孔间距为30-32-34-34时,(P)min=0.442,此时1最大。
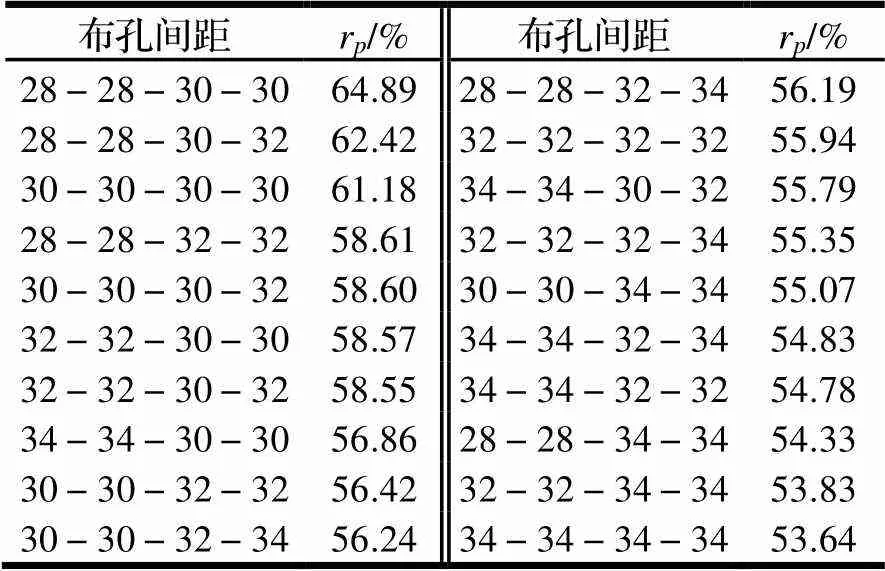
表3 等间距时,MHO-1的rp值
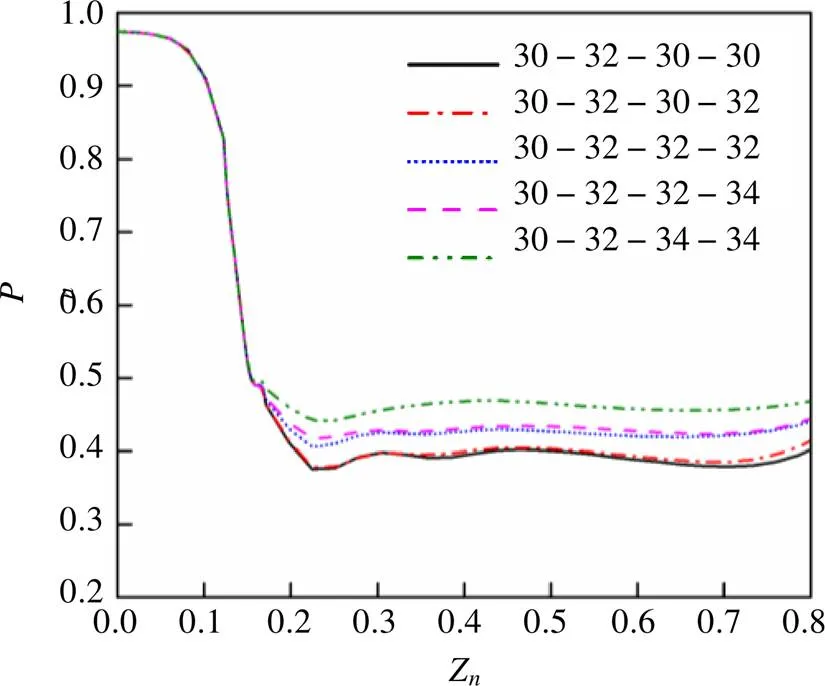
图4 MHO-1非等间距布孔对∆p1的影响
如图4所示,当MHO-1上孔中心距固定不变时,MHO-2布孔由等间距转变为非等间距后,两种布孔间距的压力曲线非常接近,如布孔间距30-32-30-30变为30-32-30-32,但是MHO-2布孔由非等间距转变为等间距后,两种布孔间距的压力曲线间隔较远,如布孔间距由30-32-30-32变为30-32-32-32。
从表4可以看出,当MHO-1上孔中心距固定不变时,1随着MHO-2上孔中心距的增大而减小,布孔间距为32-34-30-30时除外;当MHO-2上孔中心距固定不变时,1随着MHO-1上孔中心距的增大而减小,布孔间距为30-32-34-34时除外;在非等间距的MHO-1上孔中心距不变的情况下,只改变等间距的MHO-2上2c1和2c2两者任一的大小,2c1的变化比2c2的变化对1的影响明显的多,如布孔间距为30-32-30-32和30-32-32-32时,前者较后者2c1减小了2 mm、1增大了4.79%,但是布孔间距为30-32-32-34和30-32-32-32时前者较后者2c2增大了2 mm、1减少了0.57%。
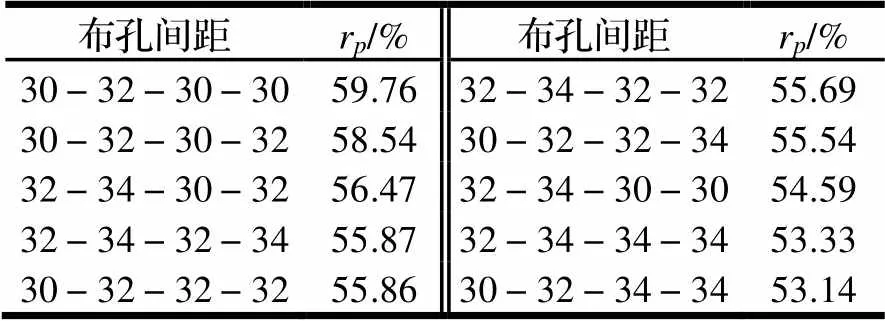
表4 非等间距时,MHO-1的rp值
在压降要求误差范围较大和孔板上开孔直径较大的情况下,通过适当缩减d2的大小,可以有效地避免孔落在对数值计算求解精度要求较高的湍流边界层内。
3 结论
(1)布孔间距对压降的影响有所不同,总体趋势是1随着MHO-1、MHO-2上孔中心距的增大而减小。
(2)MHO-1上孔中心距同时为28 mm、MHO-2上孔中心距同时为30 mm时,(P)min=0.299,此时1最大,压降效果最好。
(3)当MHO-1上孔中心距不变时,只改变等间距的MHO-2上第1层孔中心距2c1和第2层孔中心距2c2两者任一的大小,2c1的变化比2c2的变化对1的影响更加明显。
[1]Barros Filho J A,Santos AA C,Navarro MA,et a1. Effect of chamfer geometry on the pressure drop of perforated plates with thin orifices[J]. Nuclear Engineering and Design,2015(284):74-79.
[2]白兆亮,李琳. 有压管道中孔板相对间距对局部阻力系数的影响及其机理研究[J]. 水电能源科学,2015,33(1):177-182.
[3]李琳,白兆亮. 有压管道孔板局部阻力相邻影响系数研究[J]. 水电能源科学,2016,34(5):107-109,97.
[4]于洪仕,张涛,许文达. 节流孔倒角对多孔孔板流量计流场特性的影响[J]. 电子测量与仪器学报,2015,29(9):1356-1364.
[5]Yau K H,Kua E C,Balvinder S. Numerical investigation of a thick plate restriction orifice on the pressure drop performance[J]. Materials Science and Engineering,2017(243):209-215.
[6]王慧锋,凌长玺. 几何特征对多孔板特性的影响[J]. 华东理工大学学报(自然科学版),2015,41(5):677-685.
[7]HG/T 20570.15-95,管路限流孔板的设置[S]. 1996.
[8]于洪仕,张涛,葛利俊. 多孔孔板流出系数和压力损失的影响因素[J]. 化工自动化及仪表,2016,43(1):20-22.
[9]周乃君,向衍,余亚雄. 多孔均流式流量计的结构设计与特性仿真[J]. 仪表技术与传感器,2015(5):50-52.
[10]刘向红,罗毓珊,王海军. 孔板对载流管道中流致振动的影响分析[J]. 核动力工程,2013,34(S1):132-135,144.
[11]董志勇. 射流力学[M]. 北京:科学出版社,2005:98-108.
Influence of Hole Center Distance on Pressure Drop of Restriction Orifice
WANG Tianhao,JI Hua,LI Qian,DUAN Zongxing,WU Sunke
( School of Chemical Engineering, Sichuan University, Chengdu 610065, China)
The aim is to study the influence of hole center distance on the pressure drop in the multi-stage restriction orifice (MHO). Firstly, the basic structural parameters of the multi-stage restriction orifice were calculated according to the design standard. Secondly, three-dimensional numerical fluid models were established on the basis of Fluent's Standard-turbulence model. The pressure drop (1) of the first-stage restriction orifice (MHO-1), which has the greatest impact on the pressure drop was investigated. The numerical calculation results show that when the equispaced hole center distance of MHO-1 and the second-stage restriction orifice (MHO-2) is 28mm and 30mm respectively, the1is maximal. When the hole center distance of MHO-1 is certain and the equispaced hole center distance of the first and the second stage of MHO-2 are changed,2c1has greater impact on1than2c2. The general trend is that1decreases when the hole center distance increases.
restriction orifice;hole center distance;numerical calculation;pressure drop
TH703
A
10.3969/j.issn.1006-0316.2020.02.010
1006-0316 (2020) 02-0059-05
2019-08-12
四川大学德阳校市科技合作专项资金项目(2018CDDY-S18-DY)、横向项目(17H0784)
王天豪(1995-),男,河北邯郸人,硕士研究生,主要研究方向为流体机械;吉华(1972-),男,四川武胜人,博士,副教授,主要研究方向为流体机械。

